A Graph Symmetrisation Bound on Channel Information Leakage under Blowfish Privacy

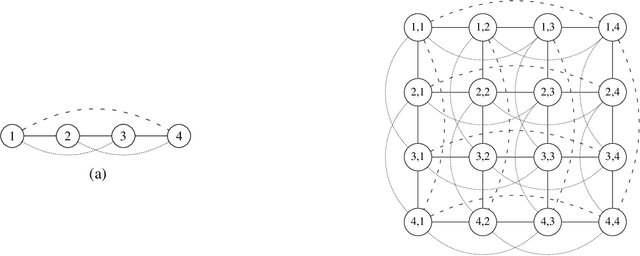
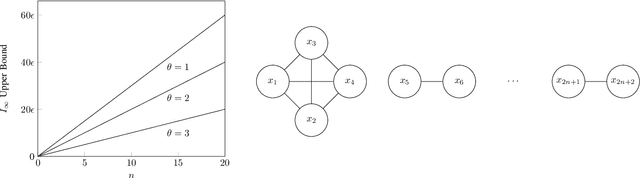
Blowfish privacy is a recent generalisation of differential privacy that enables improved utility while maintaining privacy policies with semantic guarantees, a factor that has driven the popularity of differential privacy in computer science. This paper relates Blowfish privacy to an important measure of privacy loss of information channels from the communications theory community: min-entropy leakage. Symmetry in an input data neighbouring relation is central to known connections between differential privacy and min-entropy leakage. But while differential privacy exhibits strong symmetry, Blowfish neighbouring relations correspond to arbitrary simple graphs owing to the framework's flexible privacy policies. To bound the min-entropy leakage of Blowfish-private mechanisms we organise our analysis over symmetrical partitions corresponding to orbits of graph automorphism groups. A construction meeting our bound with asymptotic equality demonstrates sharpness.

On the Differential Privacy of Bayesian Inference

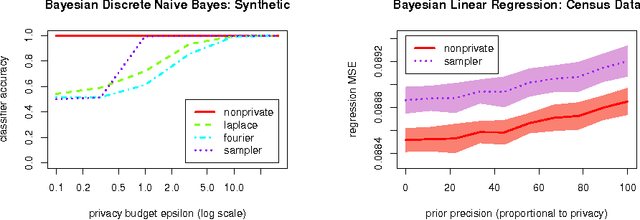
We study how to communicate findings of Bayesian inference to third parties, while preserving the strong guarantee of differential privacy. Our main contributions are four different algorithms for private Bayesian inference on proba-bilistic graphical models. These include two mechanisms for adding noise to the Bayesian updates, either directly to the posterior parameters, or to their Fourier transform so as to preserve update consistency. We also utilise a recently introduced posterior sampling mechanism, for which we prove bounds for the specific but general case of discrete Bayesian networks; and we introduce a maximum-a-posteriori private mechanism. Our analysis includes utility and privacy bounds, with a novel focus on the influence of graph structure on privacy. Worked examples and experiments with Bayesian na{\"i}ve Bayes and Bayesian linear regression illustrate the application of our mechanisms.