Corruption-Robust Lipschitz Contextual Search

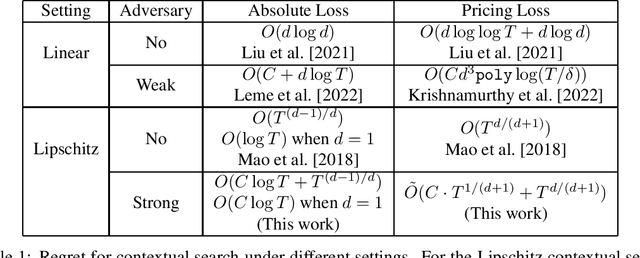
I study the problem of learning a Lipschitz function with corrupted binary signals. The learner tries to learn a Lipschitz function $f$ that the adversary chooses. In each round, the adversary selects a context vector $x_t$ in the input space, and the learner makes a guess to the true function value $f(x_t)$ and receives a binary signal indicating whether the guess was high or low. In a total of $C$ rounds, the signal may be corrupted, though the value of $C$ is unknown to the learner. The learner's goal is to incur a small cumulative loss. I present a natural yet powerful technique sanity check, which proves useful in designing corruption-robust algorithms. I design algorithms which (treating the Lipschitz parameter $L$ as constant): for the symmetric loss, the learner achieves regret $O(C\log T)$ with $d = 1$ and $O_d(C\log T + T^{(d-1)/d})$ with $d > 1$; for the pricing loss the learner achieves regret $\widetilde{O} (T^{d/(d+1)} + C\cdot T^{1/(d+1)})$.