An Improved Rapidly Exploring Random Tree Algorithm for Path Planning in Configuration Spaces with Narrow Channels

Rapidly-exploring Random Tree (RRT) algorithms have been applied successfully to challenging robot motion planning and under-actuated nonlinear control problems. However a fundamental limitation of the RRT approach is the slow convergence in configuration spaces with narrow channels because of the small probability of generating test points inside narrow channels. This paper presents an improved RRT algorithm that takes advantage of narrow channels between the initial and goal states to find shorter paths by improving the exploration of narrow regions in the configuration space. The proposed algorithm detects the presence of narrow channel by checking for collision of neighborhood points with the infeasible set and attempts to add points within narrow channels with a predetermined bias. This approach is compared with the classical RRT and its variants on a variety of benchmark planning problems. Simulation results indicate that the algorithm presented in this paper computes a significantly shorter path in spaces with narrow channels.

A Significantly Better Class of Activation Functions Than ReLU Like Activation Functions

This paper introduces a significantly better class of activation functions than the almost universally used ReLU like and Sigmoidal class of activation functions. Two new activation functions referred to as the Cone and Parabolic-Cone that differ drastically from popular activation functions and significantly outperform these on the CIFAR-10 and Imagenette benchmmarks are proposed. The cone activation functions are positive only on a finite interval and are strictly negative except at the end-points of the interval, where they become zero. Thus the set of inputs that produce a positive output for a neuron with cone activation functions is a hyperstrip and not a half-space as is the usual case. Since a hyper strip is the region between two parallel hyper-planes, it allows neurons to more finely divide the input feature space into positive and negative classes than with infinitely wide half-spaces. In particular the XOR function can be learn by a single neuron with cone-like activation functions. Both the cone and parabolic-cone activation functions are shown to achieve higher accuracies with significantly fewer neurons on benchmarks. The results presented in this paper indicate that many nonlinear real-world datasets may be separated with fewer hyperstrips than half-spaces. The Cone and Parabolic-Cone activation functions have larger derivatives than ReLU and are shown to significantly speedup training.

Computationally Efficient Quadratic Neural Networks

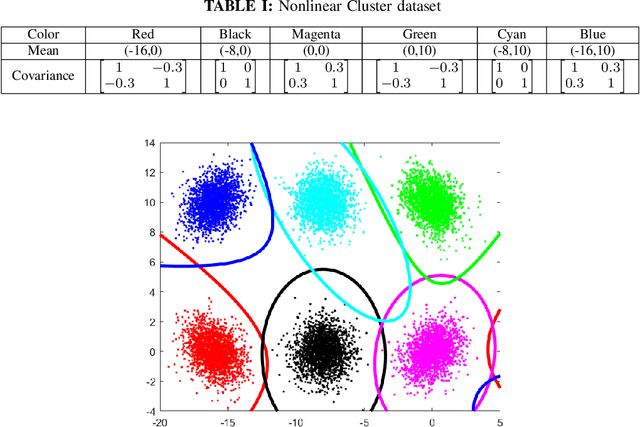
Higher order artificial neurons whose outputs are computed by applying an activation function to a higher order multinomial function of the inputs have been considered in the past, but did not gain acceptance due to the extra parameters and computational cost. However, higher order neurons have significantly greater learning capabilities since the decision boundaries of higher order neurons can be complex surfaces instead of just hyperplanes. The boundary of a single quadratic neuron can be a general hyper-quadric surface allowing it to learn many nonlinearly separable datasets. Since quadratic forms can be represented by symmetric matrices, only $\frac{n(n+1)}{2}$ additional parameters are needed instead of $n^2$. A quadratic Logistic regression model is first presented. Solutions to the XOR problem with a single quadratic neuron are considered. The complete vectorized equations for both forward and backward propagation in feedforward networks composed of quadratic neurons are derived. A reduced parameter quadratic neural network model with just $ n $ additional parameters per neuron that provides a compromise between learning ability and computational cost is presented. Comparison on benchmark classification datasets are used to demonstrate that a final layer of quadratic neurons enables networks to achieve higher accuracy with significantly fewer hidden layer neurons. In particular this paper shows that any dataset composed of $C$ bounded clusters can be separated with only a single layer of $C$ quadratic neurons.

Alternate Loss Functions Can Improve the Performance of Artificial Neural Networks

All machine learning algorithms use a loss, cost, utility or reward function to encode the learning objective and oversee the learning process. This function that supervises learning is a frequently unrecognized hyperparameter that determines how incorrect outputs are penalized and can be tuned to improve performance. This paper shows that training speed and final accuracy of neural networks can significantly depend on the loss function used to train neural networks. In particular derivative values can be significantly different with different loss functions leading to significantly different performance after gradient descent based Backpropagation (BP) training. This paper explores the effect on performance of new loss functions that are more liberal or strict compared to the popular Cross-entropy loss in penalizing incorrect outputs. Eight new loss functions are proposed and a comparison of performance with different loss functions is presented. The new loss functions presented in this paper are shown to outperform Cross-entropy loss on computer vision and NLP benchmarks.

Growing Cosine Unit: A Novel Oscillatory Activation Function That Can Speedup Training and Reduce Parameters in Convolutional Neural Networks

Convolution neural networks have been successful in solving many socially important and economically significant problems. Their ability to learn complex high-dimensional functions hierarchically can be attributed to the use of nonlinear activation functions. A key discovery that made training deep networks feasible was the adoption of the Rectified Linear Unit (ReLU) activation function to alleviate the vanishing gradient problem caused by using saturating activation functions. Since then many improved variants of the ReLU activation have been proposed. However a majority of activation functions used today are non-oscillatory and monotonically increasing due to their biological plausibility. This paper demonstrates that oscillatory activation functions can improve gradient flow and reduce network size. It is shown that oscillatory activation functions allow neurons to switch classification (sign of output) within the interior of neuronal hyperplane positive and negative half-spaces allowing complex decisions with fewer neurons. A new oscillatory activation function C(z) = z cos z that outperforms Sigmoids, Swish, Mish and ReLU on a variety of architectures and benchmarks is presented. This new activation function allows even single neurons to exhibit nonlinear decision boundaries. This paper presents a single neuron solution to the famous XOR problem. Experimental results indicate that replacing the activation function in the convolutional layers with C(z) significantly improves performance on CIFAR-10, CIFAR-100 and Imagenette.