Computationally Efficient Quadratic Neural Networks

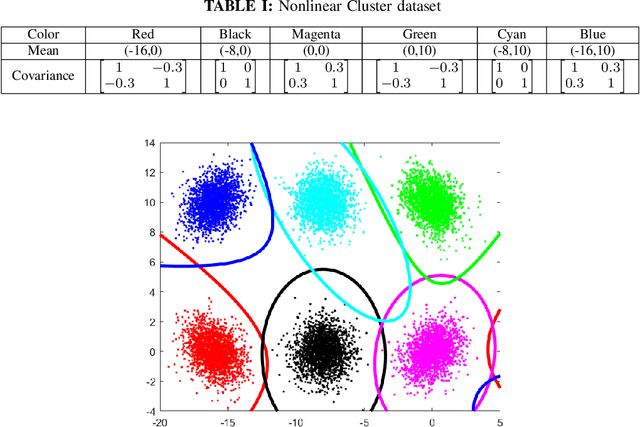
Higher order artificial neurons whose outputs are computed by applying an activation function to a higher order multinomial function of the inputs have been considered in the past, but did not gain acceptance due to the extra parameters and computational cost. However, higher order neurons have significantly greater learning capabilities since the decision boundaries of higher order neurons can be complex surfaces instead of just hyperplanes. The boundary of a single quadratic neuron can be a general hyper-quadric surface allowing it to learn many nonlinearly separable datasets. Since quadratic forms can be represented by symmetric matrices, only $\frac{n(n+1)}{2}$ additional parameters are needed instead of $n^2$. A quadratic Logistic regression model is first presented. Solutions to the XOR problem with a single quadratic neuron are considered. The complete vectorized equations for both forward and backward propagation in feedforward networks composed of quadratic neurons are derived. A reduced parameter quadratic neural network model with just $ n $ additional parameters per neuron that provides a compromise between learning ability and computational cost is presented. Comparison on benchmark classification datasets are used to demonstrate that a final layer of quadratic neurons enables networks to achieve higher accuracy with significantly fewer hidden layer neurons. In particular this paper shows that any dataset composed of $C$ bounded clusters can be separated with only a single layer of $C$ quadratic neurons.

Biologically Inspired Oscillating Activation Functions Can Bridge the Performance Gap between Biological and Artificial Neurons

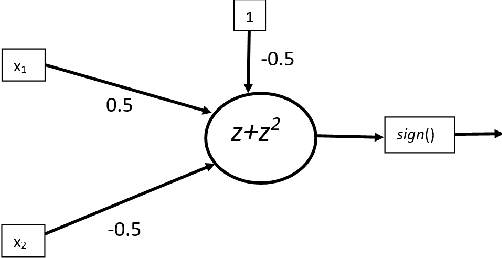
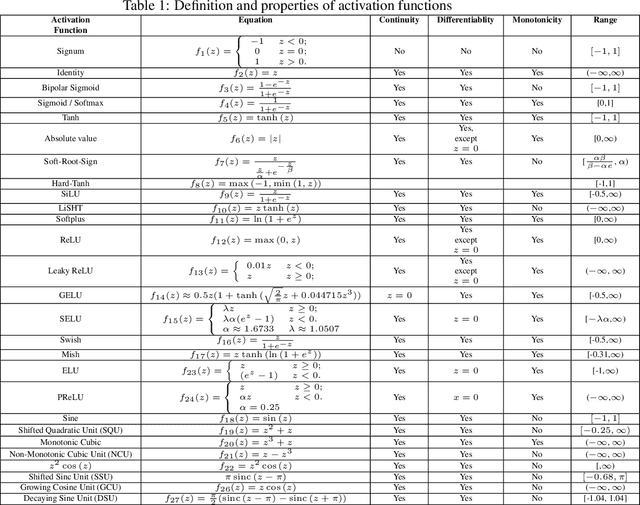
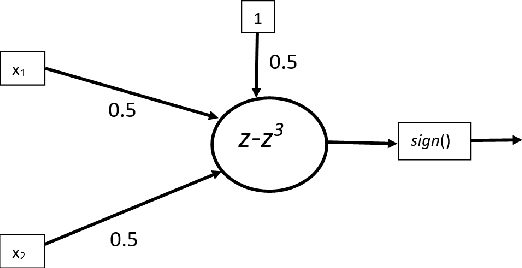
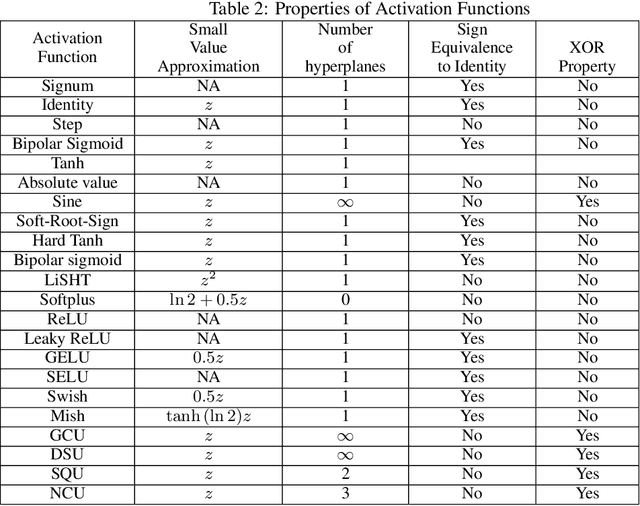
Nonlinear activation functions endow neural networks with the ability to learn complex high-dimensional functions. The choice of activation function is a crucial hyperparameter that determines the performance of deep neural networks. It significantly affects the gradient flow, speed of training and ultimately the representation power of the neural network. Saturating activation functions like sigmoids suffer from the vanishing gradient problem and cannot be used in deep neural networks. Universal approximation theorems guarantee that multilayer networks of sigmoids and ReLU can learn arbitrarily complex continuous functions to any accuracy. Despite the ability of multilayer neural networks to learn arbitrarily complex activation functions, each neuron in a conventional neural network (networks using sigmoids and ReLU like activations) has a single hyperplane as its decision boundary and hence makes a linear classification. Thus single neurons with sigmoidal, ReLU, Swish, and Mish activation functions cannot learn the XOR function. Recent research has discovered biological neurons in layers two and three of the human cortex having oscillating activation functions and capable of individually learning the XOR function. The presence of oscillating activation functions in biological neural neurons might partially explain the performance gap between biological and artificial neural networks. This paper proposes 4 new oscillating activation functions which enable individual neurons to learn the XOR function without manual feature engineering. The paper explores the possibility of using oscillating activation functions to solve classification problems with fewer neurons and reduce training time.