Optimization and Generalization Guarantees for Weight Normalization
Paper and Code
Sep 13, 2024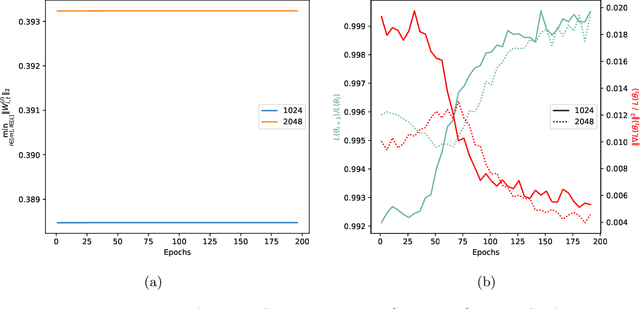
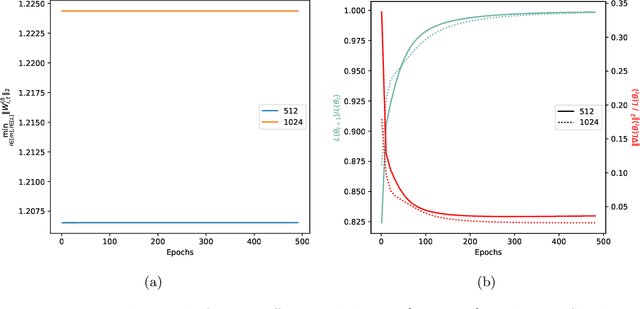
Weight normalization (WeightNorm) is widely used in practice for the training of deep neural networks and modern deep learning libraries have built-in implementations of it. In this paper, we provide the first theoretical characterizations of both optimization and generalization of deep WeightNorm models with smooth activation functions. For optimization, from the form of the Hessian of the loss, we note that a small Hessian of the predictor leads to a tractable analysis. Thus, we bound the spectral norm of the Hessian of WeightNorm networks and show its dependence on the network width and weight normalization terms--the latter being unique to networks without WeightNorm. Then, we use this bound to establish training convergence guarantees under suitable assumptions for gradient decent. For generalization, we use WeightNorm to get a uniform convergence based generalization bound, which is independent from the width and depends sublinearly on the depth. Finally, we present experimental results which illustrate how the normalization terms and other quantities of theoretical interest relate to the training of WeightNorm networks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge