Large Language Models can Achieve Social Balance

Social balance is a concept in sociology which states that if every three individuals in a population achieve certain structures of positive or negative interactions, then the whole population ends up in one faction of positive interactions or divided between two or more antagonistic factions. In this paper, we consider a group of interacting large language models (LLMs) and study how, after continuous interactions, they can achieve social balance. Across three different LLM models, we found that social balance depends on (i) whether interactions are updated based on "relationships", "appraisals", or "opinions"; (ii) whether agents update their interactions based on homophily or influence from their peers; and (iii) the number of simultaneous interactions the LLMs consider. When social balance is achieved, its particular structure of positive or negative interactions depends on these three conditions and are different across LLM models and sizes. The stability of interactions and the justification for their update also vary across models. Thus, social balance is driven by the pre-training and alignment particular to each LLM model.

Optimization and Generalization Guarantees for Weight Normalization

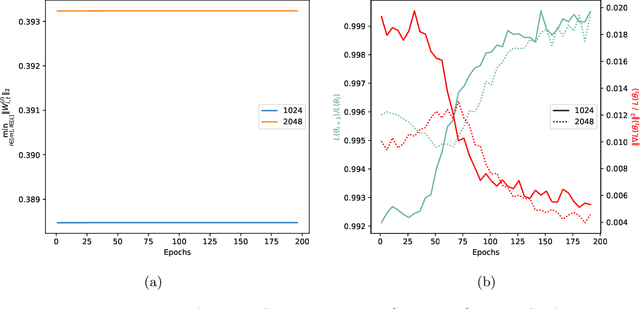
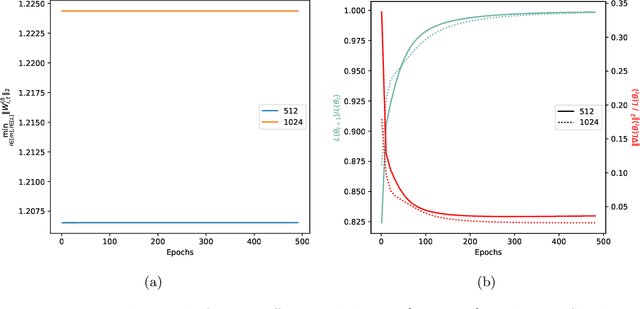
Weight normalization (WeightNorm) is widely used in practice for the training of deep neural networks and modern deep learning libraries have built-in implementations of it. In this paper, we provide the first theoretical characterizations of both optimization and generalization of deep WeightNorm models with smooth activation functions. For optimization, from the form of the Hessian of the loss, we note that a small Hessian of the predictor leads to a tractable analysis. Thus, we bound the spectral norm of the Hessian of WeightNorm networks and show its dependence on the network width and weight normalization terms--the latter being unique to networks without WeightNorm. Then, we use this bound to establish training convergence guarantees under suitable assumptions for gradient decent. For generalization, we use WeightNorm to get a uniform convergence based generalization bound, which is independent from the width and depends sublinearly on the depth. Finally, we present experimental results which illustrate how the normalization terms and other quantities of theoretical interest relate to the training of WeightNorm networks.

On the Principles behind Opinion Dynamics in Multi-Agent Systems of Large Language Models

We study the evolution of opinions inside a population of interacting large language models (LLMs). Every LLM needs to decide how much funding to allocate to an item with three initial possibilities: full, partial, or no funding. We identify biases that drive the exchange of opinions based on the LLM's tendency to (i) find consensus with the other LLM's opinion, (ii) display caution when specifying funding, and (iii) consider ethical concerns in its opinion. We find these biases are affected by the perceived absence of compelling reasons for opinion change, the perceived willingness to engage in discussion, and the distribution of allocation values. Moreover, tensions among biases can lead to the survival of funding for items with negative connotations. We also find that the final distribution of full, partial, and no funding opinions is more diverse when an LLM freely forms its opinion after an interaction than when its opinion is a multiple-choice selection among the three allocation options. In the latter case, consensus or polarization is generally attained. When agents are aware of past opinions, they seek to maintain consistency with them, and more diverse updating rules emerge. Our study is performed using a Llama 3 LLM.

Finite-sample Guarantees for Nash Q-learning with Linear Function Approximation

Nash Q-learning may be considered one of the first and most known algorithms in multi-agent reinforcement learning (MARL) for learning policies that constitute a Nash equilibrium of an underlying general-sum Markov game. Its original proof provided asymptotic guarantees and was for the tabular case. Recently, finite-sample guarantees have been provided using more modern RL techniques for the tabular case. Our work analyzes Nash Q-learning using linear function approximation -- a representation regime introduced when the state space is large or continuous -- and provides finite-sample guarantees that indicate its sample efficiency. We find that the obtained performance nearly matches an existing efficient result for single-agent RL under the same representation and has a polynomial gap when compared to the best-known result for the tabular case.

Restricted Strong Convexity of Deep Learning Models with Smooth Activations

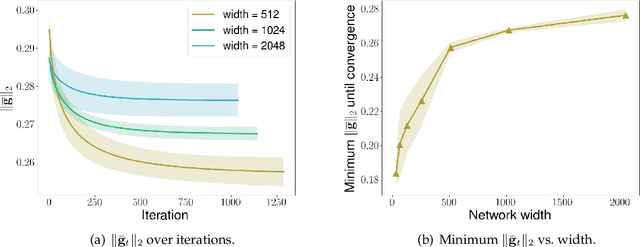
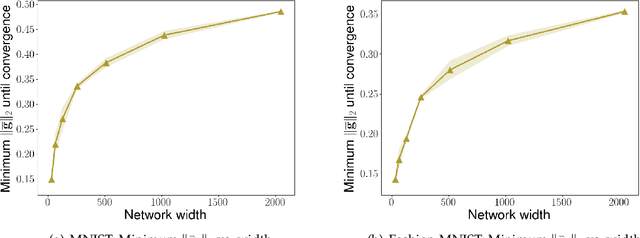
We consider the problem of optimization of deep learning models with smooth activation functions. While there exist influential results on the problem from the ``near initialization'' perspective, we shed considerable new light on the problem. In particular, we make two key technical contributions for such models with $L$ layers, $m$ width, and $\sigma_0^2$ initialization variance. First, for suitable $\sigma_0^2$, we establish a $O(\frac{\text{poly}(L)}{\sqrt{m}})$ upper bound on the spectral norm of the Hessian of such models, considerably sharpening prior results. Second, we introduce a new analysis of optimization based on Restricted Strong Convexity (RSC) which holds as long as the squared norm of the average gradient of predictors is $\Omega(\frac{\text{poly}(L)}{\sqrt{m}})$ for the square loss. We also present results for more general losses. The RSC based analysis does not need the ``near initialization" perspective and guarantees geometric convergence for gradient descent (GD). To the best of our knowledge, ours is the first result on establishing geometric convergence of GD based on RSC for deep learning models, thus becoming an alternative sufficient condition for convergence that does not depend on the widely-used Neural Tangent Kernel (NTK). We share preliminary experimental results supporting our theoretical advances.

Discrete State-Action Abstraction via the Successor Representation

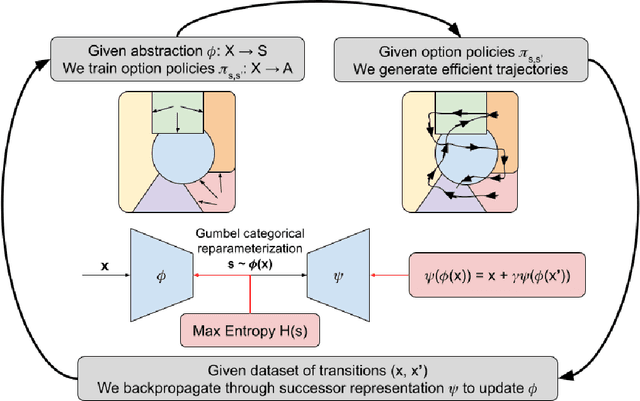
When reinforcement learning is applied with sparse rewards, agents must spend a prohibitively long time exploring the unknown environment without any learning signal. Abstraction is one approach that provides the agent with an intrinsic reward for transitioning in a latent space. Prior work focuses on dense continuous latent spaces, or requires the user to manually provide the representation. Our approach is the first for automatically learning a discrete abstraction of the underlying environment. Moreover, our method works on arbitrary input spaces, using an end-to-end trainable regularized successor representation model. For transitions between abstract states, we train a set of temporally extended actions in the form of options, i.e., an action abstraction. Our proposed algorithm, Discrete State-Action Abstraction (DSAA), iteratively swaps between training these options and using them to efficiently explore more of the environment to improve the state abstraction. As a result, our model is not only useful for transfer learning but also in the online learning setting. We empirically show that our agent is able to explore the environment and solve provided tasks more efficiently than baseline reinforcement learning algorithms. Our code is publicly available at \url{https://github.com/amnonattali/dsaa}.

One Policy is Enough: Parallel Exploration with a Single Policy is Minimax Optimal for Reward-Free Reinforcement Learning

While parallelism has been extensively used in Reinforcement Learning (RL), the quantitative effects of parallel exploration are not well understood theoretically. We study the benefits of simple parallel exploration for reward-free RL for linear Markov decision processes (MDPs) and two-player zero-sum Markov games (MGs). In contrast to the existing literature focused on approaches that encourage agents to explore over a diverse set of policies, we show that using a single policy to guide exploration across all agents is sufficient to obtain an almost-linear speedup in all cases compared to their fully sequential counterpart. Further, we show that this simple procedure is minimax optimal up to logarithmic factors in the reward-free setting for both linear MDPs and two-player zero-sum MGs. From a practical perspective, our paper shows that a single policy is sufficient and provably optimal for incorporating parallelism during the exploration phase.

A Contraction Theory Approach to Optimization Algorithms from Acceleration Flows

Much recent interest has focused on the design of optimization algorithms from the discretization of an associated optimization flow, i.e., a system of differential equations (ODEs) whose trajectories solve an associated optimization problem. Such a design approach poses an important problem: how to find a principled methodology to design and discretize appropriate ODEs. This paper aims to provide a solution to this problem through the use of contraction theory. We first introduce general mathematical results that explain how contraction theory guarantees the stability of the implicit and explicit Euler integration methods. Then, we propose a novel system of ODEs, namely the Accelerated-Contracting-Nesterov flow, and use contraction theory to establish it is an optimization flow with exponential convergence rate, from which the linear convergence rate of its associated optimization algorithm is immediately established. Remarkably, a simple explicit Euler discretization of this flow corresponds to the Nesterov acceleration method. Finally, we present how our approach leads to performance guarantees in the design of optimization algorithms for time-varying optimization problems.

Distributionally Robust Formulation and Model Selection for the Graphical Lasso

Building on a recent framework for distributionally robust optimization in machine learning, we develop a similar framework for estimation of the inverse covariance matrix for multivariate data. We provide a novel notion of a Wasserstein ambiguity set specifically tailored to this estimation problem, from which we obtain a representation for a tractable class of regularized estimators. Special cases include penalized likelihood estimators for Gaussian data, specifically the graphical lasso estimator. As a consequence of this formulation, a natural relationship arises between the radius of the Wasserstein ambiguity set and the regularization parameter in the estimation problem. Using this relationship, one can directly control the level of robustness of the estimation procedure by specifying a desired level of confidence with which the ambiguity set contains a distribution with the true population covariance. Furthermore, a unique feature of our formulation is that the radius can be expressed in closed-form as a function of the ordinary sample covariance matrix. Taking advantage of this finding, we develop a simple algorithm to determine a regularization parameter for graphical lasso, using only the bootstrapped sample covariance matrices, meaning that computationally expensive repeated evaluation of the graphical lasso algorithm is not necessary. Alternatively, the distributionally robust formulation can also quantify the robustness of the corresponding estimator if one uses an off-the-shelf method such as cross-validation. Finally, we numerically study the obtained regularization criterion and analyze the robustness of other automated tuning procedures used in practice.