Nancy M. Amato
Quick Heuristic Validation of Edges in Dynamic Roadmap Graphs
Jan 28, 2026Abstract:In this paper we tackle the problem of adjusting roadmap graphs for robot motion planning to non-static environments. We introduce the "Red-Green-Gray" paradigm, a modification of the SPITE method, capable of classifying the validity status of nodes and edges using cheap heuristic checks, allowing fast semi-lazy roadmap updates. Given a roadmap, we use simple computational geometry methods to approximate the swept volumes of robots and perform lazy collision checks, and label a subset of the edges as invalid (red), valid (green), or unknown (gray). We present preliminary experimental results comparing our method to the well-established technique of Leven and Hutchinson, and showing increased accuracy as well as the ability to correctly label edges as invalid while maintaining comparable update runtimes.
Edge Nearest Neighbor in Sampling-Based Motion Planning
Jun 16, 2025Abstract:Neighborhood finders and nearest neighbor queries are fundamental parts of sampling based motion planning algorithms. Using different distance metrics or otherwise changing the definition of a neighborhood produces different algorithms with unique empiric and theoretical properties. In \cite{l-pa-06} LaValle suggests a neighborhood finder for the Rapidly-exploring Random Tree RRT algorithm \cite{l-rrtnt-98} which finds the nearest neighbor of the sampled point on the swath of the tree, that is on the set of all of the points on the tree edges, using a hierarchical data structure. In this paper we implement such a neighborhood finder and show, theoretically and experimentally, that this results in more efficient algorithms, and suggest a variant of the Rapidly-exploring Random Graph RRG algorithm \cite{f-isaom-10} that better exploits the exploration properties of the newly described subroutine for finding narrow passages.
PRISM: Complete Online Decentralized Multi-Agent Pathfinding with Rapid Information Sharing using Motion Constraints
May 12, 2025Abstract:We introduce PRISM (Pathfinding with Rapid Information Sharing using Motion Constraints), a decentralized algorithm designed to address the multi-task multi-agent pathfinding (MT-MAPF) problem. PRISM enables large teams of agents to concurrently plan safe and efficient paths for multiple tasks while avoiding collisions. It employs a rapid communication strategy that uses information packets to exchange motion constraint information, enhancing cooperative pathfinding and situational awareness, even in scenarios without direct communication. We prove that PRISM resolves and avoids all deadlock scenarios when possible, a critical challenge in decentralized pathfinding. Empirically, we evaluate PRISM across five environments and 25 random scenarios, benchmarking it against the centralized Conflict-Based Search (CBS) and the decentralized Token Passing with Task Swaps (TPTS) algorithms. PRISM demonstrates scalability and solution quality, supporting 3.4 times more agents than CBS and handling up to 2.5 times more tasks in narrow passage environments than TPTS. Additionally, PRISM matches CBS in solution quality while achieving faster computation times, even under low-connectivity conditions. Its decentralized design reduces the computational burden on individual agents, making it scalable for large environments. These results confirm PRISM's robustness, scalability, and effectiveness in complex and dynamic pathfinding scenarios.
Path Database Guidance for Motion Planning
Apr 07, 2025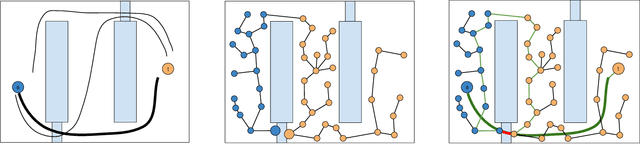

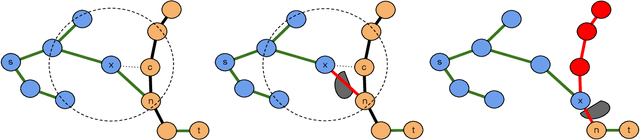
Abstract:One approach to using prior experience in robot motion planning is to store solutions to previously seen problems in a database of paths. Methods that use such databases are characterized by how they query for a path and how they use queries given a new problem. In this work we present a new method, Path Database Guidance (PDG), which innovates on existing work in two ways. First, we use the database to compute a heuristic for determining which nodes of a search tree to expand, in contrast to prior work which generally pastes the (possibly transformed) queried path or uses it to bias a sampling distribution. We demonstrate that this makes our method more easily composable with other search methods by dynamically interleaving exploration according to a baseline algorithm with exploitation of the database guidance. Second, in contrast to other methods that treat the database as a single fixed prior, our database (and thus our queried heuristic) updates as we search the implicitly defined robot configuration space. We experimentally demonstrate the effectiveness of PDG in a variety of explicitly defined environment distributions in simulation.
Lazy-DaSH: Lazy Approach for Hypergraph-based Multi-robot Task and Motion Planning
Apr 07, 2025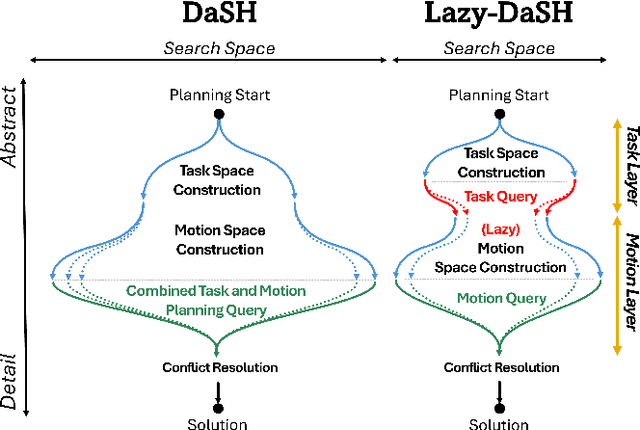
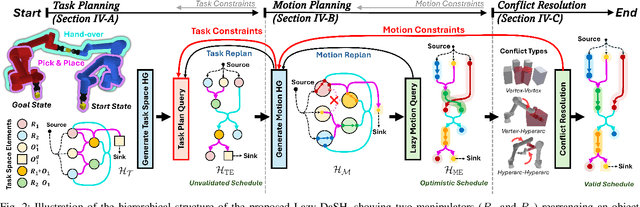
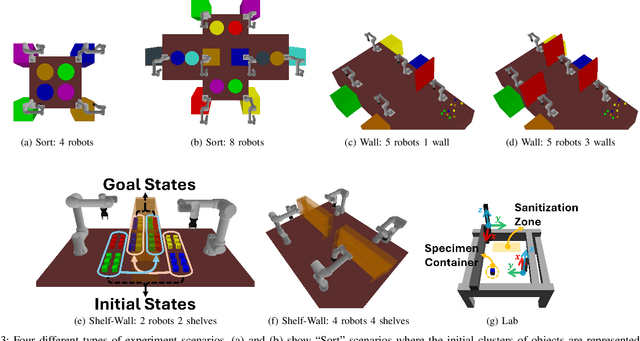

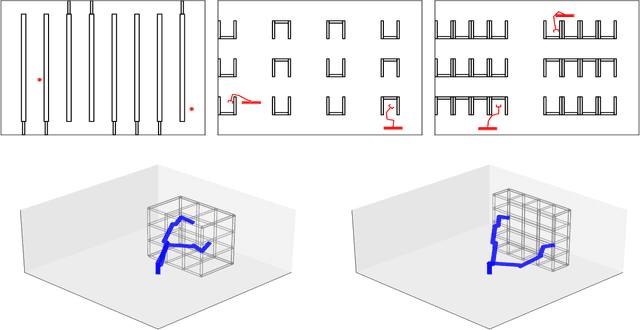
Abstract:We introduce Lazy-DaSH, an improvement over the recent state of the art multi-robot task and motion planning method DaSH, which scales to more than double the number of robots and objects compared to the original method and achieves an order of magnitude faster planning time when applied to a multi-manipulator object rearrangement problem. We achieve this improvement through a hierarchical approach, where a high-level task planning layer identifies planning spaces required for task completion, and motion feasibility is validated lazily only within these spaces. In contrast, DaSH precomputes the motion feasibility of all possible actions, resulting in higher costs for constructing state space representations. Lazy-DaSH maintains efficient query performance by utilizing a constraint feedback mechanism within its hierarchical structure, ensuring that motion feasibility is effectively conveyed to the query process. By maintaining smaller state space representations, our method significantly reduces both representation construction time and query time. We evaluate Lazy-DaSH in four distinct scenarios, demonstrating its scalability to increasing numbers of robots and objects, as well as its adaptability in resolving conflicts through the constraint feedback mechanism.
K-ARC: Adaptive Robot Coordination for Multi-Robot Kinodynamic Planning
Jan 02, 2025



Abstract:This work presents Kinodynamic Adaptive Robot Coordination (K-ARC), a novel algorithm for multi-robot kinodynamic planning. Our experimental results show the capability of K-ARC to plan for up to 32 planar mobile robots, while achieving up to an order of magnitude of speed-up compared to previous methods in various scenarios. K-ARC is able to achieve this due to its two main properties. First, K-ARC constructs its solution iteratively by planning in segments, where initial kinodynamic paths are found through optimization-based approaches and the inter-robot conflicts are resolved through sampling-based approaches. The interleaving use of sampling-based and optimization-based approaches allows K-ARC to leverage the strengths of both approaches in different sections of the planning process where one is more suited than the other, while previous methods tend to emphasize on one over the other. Second, K-ARC builds on a previously proposed multi-robot motion planning framework, Adaptive Robot Coordination (ARC), and inherits its strength of focusing on coordination between robots only when needed, saving computation efforts. We show how the combination of these two properties allows K-ARC to achieve overall better performance in our simulated experiments with increasing numbers of robots, increasing degrees of problem difficulties, and increasing complexities of robot dynamics.
Experience-based Subproblem Planning for Multi-Robot Motion Planning
Nov 13, 2024



Abstract:Multi-robot systems enhance efficiency and productivity across various applications, from manufacturing to surveillance. While single-robot motion planning has improved by using databases of prior solutions, extending this approach to multi-robot motion planning (MRMP) presents challenges due to the increased complexity and diversity of tasks and configurations. Recent discrete methods have attempted to address this by focusing on relevant lower-dimensional subproblems, but they are inadequate for complex scenarios like those involving manipulator robots. To overcome this, we propose a novel approach that %leverages experience-based planning by constructs and utilizes databases of solutions for smaller sub-problems. By focusing on interactions between fewer robots, our method reduces the need for exhaustive database growth, allowing for efficient handling of more complex MRMP scenarios. We validate our approach with experiments involving both mobile and manipulator robots, demonstrating significant improvements over existing methods in scalability and planning efficiency. Our contributions include a rapidly constructed database for low-dimensional MRMP problems, a framework for applying these solutions to larger problems, and experimental validation with up to 32 mobile and 16 manipulator robots.
Encoding Reusable Multi-Robot Planning Strategies as Abstract Hypergraphs
Sep 16, 2024


Abstract:Multi-Robot Task Planning (MR-TP) is the search for a discrete-action plan a team of robots should take to complete a task. The complexity of such problems scales exponentially with the number of robots and task complexity, making them challenging for online solution. To accelerate MR-TP over a system's lifetime, this work looks at combining two recent advances: (i) Decomposable State Space Hypergraph (DaSH), a novel hypergraph-based framework to efficiently model and solve MR-TP problems; and \mbox{(ii) learning-by-abstraction,} a technique that enables automatic extraction of generalizable planning strategies from individual planning experiences for later reuse. Specifically, we wish to extend this strategy-learning technique, originally designed for single-robot planning, to benefit multi-robot planning using hypergraph-based MR-TP.
SPITE: Simple Polyhedral Intersection Techniques for modified Environments
Jun 28, 2024
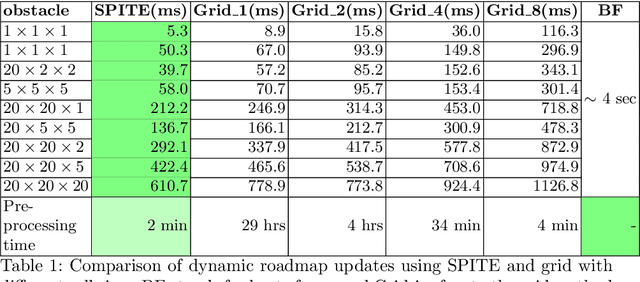

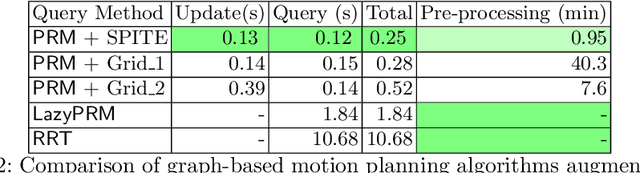
Abstract:Motion planning in modified environments is a challenging task, as it compounds the innate difficulty of the motion planning problem with a changing environment. This renders some algorithmic methods such as probabilistic roadmaps less viable, as nodes and edges may become invalid as a result of these changes. In this paper, we present a method of transforming any configuration space graph, such as a roadmap, to a dynamic data structure capable of updating the validity of its nodes and edges in response to discrete changes in obstacle positions. We use methods from computational geometry to compute 3D swept volume approximations of configuration space points and curves to achieve 10-40 percent faster updates and up to 60 percent faster motion planning queries than previous algorithms while requiring a significantly shorter pre-processing phase, requiring minutes instead of hours needed by the competing method to achieve somewhat similar update times.
A Framework for Guided Motion Planning
Apr 04, 2024Abstract:Randomized sampling based algorithms are widely used in robot motion planning due to the problem's intractability, and are experimentally effective on a wide range of problem instances. Most variants bias their sampling using various heuristics related to the known underlying structure of the search space. In this work, we formalize the intuitive notion of guided search by defining the concept of a guiding space. This new language encapsulates many seemingly distinct prior methods under the same framework, and allows us to reason about guidance, a previously obscured core contribution of different algorithms. We suggest an information theoretic method to evaluate guidance, which experimentally matches intuition when tested on known algorithms in a variety of environments. The language and evaluation of guidance suggests improvements to existing methods, and allows for simple hybrid algorithms that combine guidance from multiple sources.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge