TIDE: A Trace-Informed Depth-First Exploration for Planning with Temporally Extended Goals

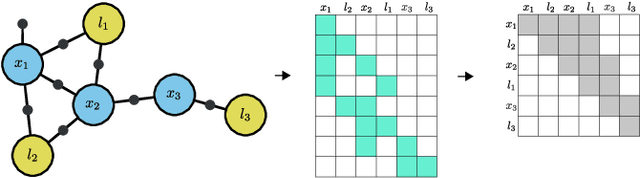
Task planning with temporally extended goals (TEGs) is a critical challenge in AI and robotics, enabling agents to achieve complex sequences of objectives over time rather than addressing isolated, immediate tasks. Linear Temporal Logic on finite traces (LTLf ) provides a robust formalism for encoding these temporal goals. Traditional LTLf task planning approaches often transform the temporal planning problem into a classical planning problem with reachability goals, which are then solved using off-the-shelf planners. However, these methods often lack informed heuristics to provide a guided search for temporal goals. We introduce TIDE (Trace-Informed Depth-first Exploration), a novel approach that addresses this limitation by decomposing a temporal problem into a sequence of smaller, manageable reach-avoid sub-problems, each solvable using an off-the-shelf planner. TIDE identifies and prioritizes promising automaton traces within the domain graph, using cost-driven heuristics to guide exploration. Its adaptive backtracking mechanism systematically recovers from failed plans by recalculating costs and penalizing infeasible transitions, ensuring completeness and efficiency. Experimental results demonstrate that TIDE achieves promising performance and is a valuable addition to the portfolio of planning methods for temporally extended goals.

Falsification of Autonomous Systems in Rich Environments

Validating the behavior of autonomous Cyber-Physical Systems (CPS) and Artificial Intelligence (AI) agents, which rely on automated controllers, is an objective of great importance. In recent years, Neural-Network (NN) controllers have been demonstrating great promise. Unfortunately, such learned controllers are often not certified and can cause the system to suffer from unpredictable or unsafe behavior. To mitigate this issue, a great effort has been dedicated to automated verification of systems. Specifically, works in the category of ``black-box testing'' rely on repeated system simulations to find a falsifying counterexample of a system run that violates a specification. As running high-fidelity simulations is computationally demanding, the goal of falsification approaches is to minimize the simulation effort (NN inference queries) needed to return a falsifying example. This often proves to be a great challenge, especially when the tested controller is well-trained. This work contributes a novel falsification approach for autonomous systems under formal specification operating in uncertain environments. We are especially interested in CPS operating in rich, semantically-defined, open environments, which yield high-dimensional, simulation-dependent sensor observations. Our approach introduces a novel reformulation of the falsification problem as the problem of planning a trajectory for a ``meta-system,'' which wraps and encapsulates the examined system; we call this approach: meta-planning. This formulation can be solved with standard sampling-based motion-planning techniques (like RRT) and can gradually integrate domain knowledge to improve the search. We support the suggested approach with an experimental study on falsification of an obstacle-avoiding autonomous car with a NN controller, where meta-planning demonstrates superior performance over alternative approaches.

Encoding Reusable Multi-Robot Planning Strategies as Abstract Hypergraphs

Multi-Robot Task Planning (MR-TP) is the search for a discrete-action plan a team of robots should take to complete a task. The complexity of such problems scales exponentially with the number of robots and task complexity, making them challenging for online solution. To accelerate MR-TP over a system's lifetime, this work looks at combining two recent advances: (i) Decomposable State Space Hypergraph (DaSH), a novel hypergraph-based framework to efficiently model and solve MR-TP problems; and \mbox{(ii) learning-by-abstraction,} a technique that enables automatic extraction of generalizable planning strategies from individual planning experiences for later reuse. Specifically, we wish to extend this strategy-learning technique, originally designed for single-robot planning, to benefit multi-robot planning using hypergraph-based MR-TP.

Efficient Belief Space Planning in High-Dimensional State Spaces using PIVOT: Predictive Incremental Variable Ordering Tactic

In this work, we examine the problem of online decision making under uncertainty, which we formulate as planning in the belief space. Maintaining beliefs (i.e., distributions) over high-dimensional states (e.g., entire trajectories) was not only shown to significantly improve accuracy, but also allows planning with information-theoretic objectives, as required for the tasks of active SLAM and information gathering. Nonetheless, planning under this "smoothing" paradigm holds a high computational complexity, which makes it challenging for online solution. Thus, we suggest the following idea: before planning, perform a standalone state variable reordering procedure on the initial belief, and "push forwards" all the predicted loop closing variables. Since the initial variable order determines which subset of them would be affected by incoming updates, such reordering allows us to minimize the total number of affected variables, and reduce the computational complexity of candidate evaluation during planning. We call this approach PIVOT: Predictive Incremental Variable Ordering Tactic. Applying this tactic can also improve the state inference efficiency; if we maintain the PIVOT order after the planning session, then we should similarly reduce the cost of loop closures, when they actually occur. To demonstrate its effectiveness, we applied PIVOT in a realistic active SLAM simulation, where we managed to significantly reduce the computation time of both the planning and inference sessions. The approach is applicable to general distributions, and induces no loss in accuracy.

Efficient Decision Making and Belief Space Planning using Sparse Approximations

In this work, we introduce a new approach for the efficient solution of autonomous decision and planning problems, with a special focus on decision making under uncertainty and belief space planning (BSP) in high-dimensional state spaces. Usually, to solve the decision problem, we identify the optimal action, according to some objective function. Instead, we claim that we can sometimes generate and solve an analogous yet simplified decision problem, which can be solved more efficiently. Furthermore, a wise simplification method can lead to the same action selection, or one for which the maximal loss can be guaranteed. This simplification is separated from the state inference, and does not compromise its accuracy, as the selected action would finally be applied on the original state. At first, we develop the concept for general decision problems, and provide a theoretical framework of definitions to allow a coherent discussion. We then practically apply these ideas to BSP problems, in which the problem is simplified by considering a sparse approximation of the initial belief. The scalable sparsification algorithm we provide is able to yield solutions which are guaranteed to be consistent with the original problem. We demonstrate the benefits of the approach in the solution of a highly realistic active-SLAM problem, and manage to significantly reduce computation time, with practically no loss in the quality of solution. This rigorous and fundamental work is conceptually novel, and holds numerous possible extensions.