Error Bounds for Deep Learning-based Uncertainty Propagation in SDEs

Stochastic differential equations are commonly used to describe the evolution of stochastic processes. The uncertainty of such processes is best represented by the probability density function (PDF), whose evolution is governed by the Fokker-Planck partial differential equation (FP-PDE). However, it is generally infeasible to solve the FP-PDE in closed form. In this work, we show that physics-informed neural networks (PINNs) can be trained to approximate the solution PDF using existing methods. The main contribution is the analysis of the approximation error: we develop a theory to construct an arbitrary tight error bound with PINNs. In addition, we derive a practical error bound that can be efficiently constructed with existing training methods. Finally, we explain that this error-bound theory generalizes to approximate solutions of other linear PDEs. Several numerical experiments are conducted to demonstrate and validate the proposed methods.

Learning-Based Shielding for Safe Autonomy under Unknown Dynamics

Shielding is a common method used to guarantee the safety of a system under a black-box controller, such as a neural network controller from deep reinforcement learning (DRL), with simpler, verified controllers. Existing shielding methods rely on formal verification through Markov Decision Processes (MDPs), assuming either known or finite-state models, which limits their applicability to DRL settings with unknown, continuous-state systems. This paper addresses these limitations by proposing a data-driven shielding methodology that guarantees safety for unknown systems under black-box controllers. The approach leverages Deep Kernel Learning to model the systems' one-step evolution with uncertainty quantification and constructs a finite-state abstraction as an Interval MDP (IMDP). By focusing on safety properties expressed in safe linear temporal logic (safe LTL), we develop an algorithm that computes the maximally permissive set of safe policies on the IMDP, ensuring avoidance of unsafe states. The algorithms soundness and computational complexity are demonstrated through theoretical proofs and experiments on nonlinear systems, including a high-dimensional autonomous spacecraft scenario.

Admissibility Over Winning: A New Approach to Reactive Synthesis in Robotics

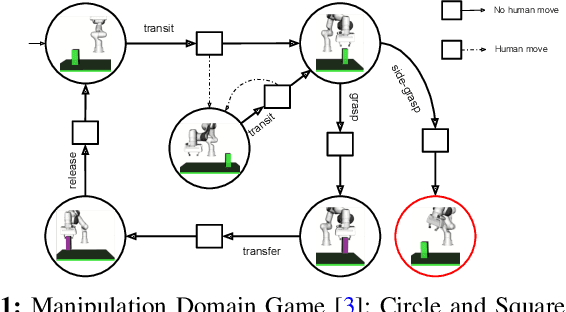
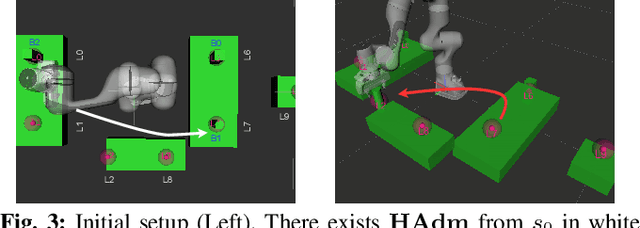
Reactive synthesis is a framework for modeling and automatically synthesizing strategies in robotics, typically through computing a \emph{winning} strategy in a 2-player game between the robot and the environment. Winning strategies, however, do not always exist, even in some simple cases. In such situations, it is still desirable for the robot to attempt its task rather than "giving up". In this work, we explore the notion of admissibility to define strategies beyond winning, tailored specifically for robotic systems. We introduce an ordering of admissible strategies and define \emph{admissibly rational strategies}, which aim to be winning and cooperative when possible, and non-violating and hopeful when necessary. We present an efficient synthesis algorithm and demonstrate that admissibly rational strategies produce desirable behaviors through case studies.

Kino-PAX: Highly Parallel Kinodynamic Sampling-based Planner

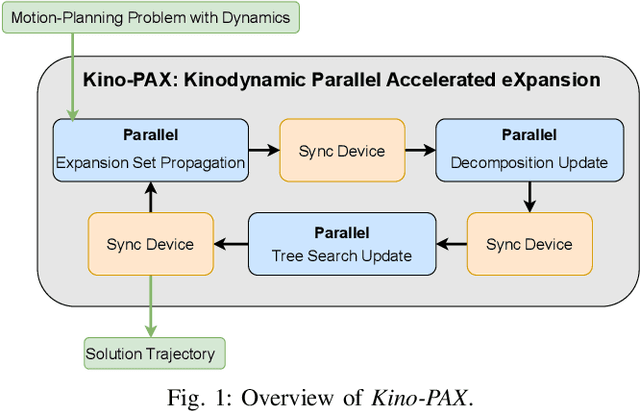
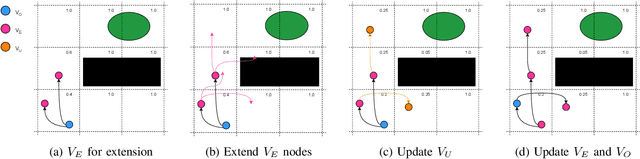
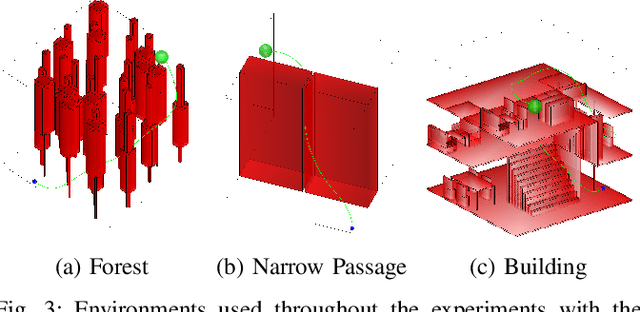
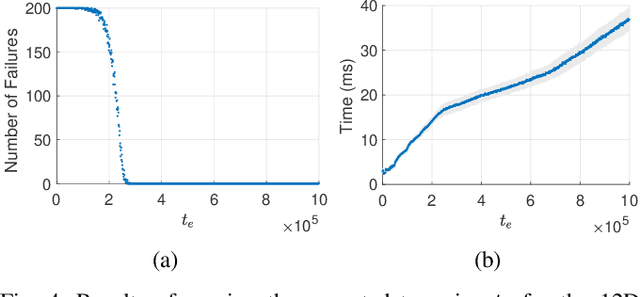
Sampling-based motion planners (SBMPs) are effective for planning with complex kinodynamic constraints in high-dimensional spaces, but they still struggle to achieve real-time performance, which is mainly due to their serial computation design. We present Kinodynamic Parallel Accelerated eXpansion (Kino-PAX), a novel highly parallel kinodynamic SBMP designed for parallel devices such as GPUs. Kino-PAX grows a tree of trajectory segments directly in parallel. Our key insight is how to decompose the iterative tree growth process into three massively parallel subroutines. Kino-PAX is designed to align with the parallel device execution hierarchies, through ensuring that threads are largely independent, share equal workloads, and take advantage of low-latency resources while minimizing high-latency data transfers and process synchronization. This design results in a very efficient GPU implementation. We prove that Kino-PAX is probabilistically complete and analyze its scalability with compute hardware improvements. Empirical evaluations demonstrate solutions in the order of 10 ms on a desktop GPU and in the order of 100 ms on an embedded GPU, representing up to 1000 times improvement compared to coarse-grained CPU parallelization of state-of-the-art sequential algorithms over a range of complex environments and systems.

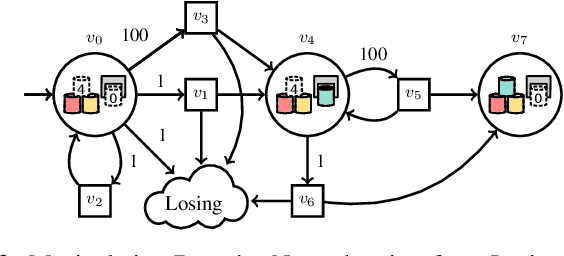
Beyond Winning Strategies: Admissible and Admissible Winning Strategies for Quantitative Reachability Games

Classical reactive synthesis approaches aim to synthesize a reactive system that always satisfies a given specifications. These approaches often reduce to playing a two-player zero-sum game where the goal is to synthesize a winning strategy. However, in many pragmatic domains, such as robotics, a winning strategy does not always exist, yet it is desirable for the system to make an effort to satisfy its requirements instead of "giving up". To this end, this paper investigates the notion of admissible strategies, which formalize "doing-your-best", in quantitative reachability games. We show that, unlike the qualitative case, quantitative admissible strategies are history-dependent even for finite payoff functions, making synthesis a challenging task. In addition, we prove that admissible strategies always exist but may produce undesirable optimistic behaviors. To mitigate this, we propose admissible winning strategies, which enforce the best possible outcome while being admissible. We show that both strategies always exist but are not memoryless. We provide necessary and sufficient conditions for the existence of both strategies and propose synthesis algorithms. Finally, we illustrate the strategies on gridworld and robot manipulator domains.

Error Bounds For Gaussian Process Regression Under Bounded Support Noise With Applications To Safety Certification

Gaussian Process Regression (GPR) is a powerful and elegant method for learning complex functions from noisy data with a wide range of applications, including in safety-critical domains. Such applications have two key features: (i) they require rigorous error quantification, and (ii) the noise is often bounded and non-Gaussian due to, e.g., physical constraints. While error bounds for applying GPR in the presence of non-Gaussian noise exist, they tend to be overly restrictive and conservative in practice. In this paper, we provide novel error bounds for GPR under bounded support noise. Specifically, by relying on concentration inequalities and assuming that the latent function has low complexity in the reproducing kernel Hilbert space (RKHS) corresponding to the GP kernel, we derive both probabilistic and deterministic bounds on the error of the GPR. We show that these errors are substantially tighter than existing state-of-the-art bounds and are particularly well-suited for GPR with neural network kernels, i.e., Deep Kernel Learning (DKL). Furthermore, motivated by applications in safety-critical domains, we illustrate how these bounds can be combined with stochastic barrier functions to successfully quantify the safety probability of an unknown dynamical system from finite data. We validate the efficacy of our approach through several benchmarks and comparisons against existing bounds. The results show that our bounds are consistently smaller, and that DKLs can produce error bounds tighter than sample noise, significantly improving the safety probability of control systems.

Finite Neural Networks as Mixtures of Gaussian Processes: From Provable Error Bounds to Prior Selection

Infinitely wide or deep neural networks (NNs) with independent and identically distributed (i.i.d.) parameters have been shown to be equivalent to Gaussian processes. Because of the favorable properties of Gaussian processes, this equivalence is commonly employed to analyze neural networks and has led to various breakthroughs over the years. However, neural networks and Gaussian processes are equivalent only in the limit; in the finite case there are currently no methods available to approximate a trained neural network with a Gaussian model with bounds on the approximation error. In this work, we present an algorithmic framework to approximate a neural network of finite width and depth, and with not necessarily i.i.d. parameters, with a mixture of Gaussian processes with error bounds on the approximation error. In particular, we consider the Wasserstein distance to quantify the closeness between probabilistic models and, by relying on tools from optimal transport and Gaussian processes, we iteratively approximate the output distribution of each layer of the neural network as a mixture of Gaussian processes. Crucially, for any NN and $\epsilon >0$ our approach is able to return a mixture of Gaussian processes that is $\epsilon$-close to the NN at a finite set of input points. Furthermore, we rely on the differentiability of the resulting error bound to show how our approach can be employed to tune the parameters of a NN to mimic the functional behavior of a given Gaussian process, e.g., for prior selection in the context of Bayesian inference. We empirically investigate the effectiveness of our results on both regression and classification problems with various neural network architectures. Our experiments highlight how our results can represent an important step towards understanding neural network predictions and formally quantifying their uncertainty.

Online Pareto-Optimal Decision-Making for Complex Tasks using Active Inference

When a robot autonomously performs a complex task, it frequently must balance competing objectives while maintaining safety. This becomes more difficult in uncertain environments with stochastic outcomes. Enhancing transparency in the robot's behavior and aligning with user preferences are also crucial. This paper introduces a novel framework for multi-objective reinforcement learning that ensures safe task execution, optimizes trade-offs between objectives, and adheres to user preferences. The framework has two main layers: a multi-objective task planner and a high-level selector. The planning layer generates a set of optimal trade-off plans that guarantee satisfaction of a temporal logic task. The selector uses active inference to decide which generated plan best complies with user preferences and aids learning. Operating iteratively, the framework updates a parameterized learning model based on collected data. Case studies and benchmarks on both manipulation and mobile robots show that our framework outperforms other methods and (i) learns multiple optimal trade-offs, (ii) adheres to a user preference, and (iii) allows the user to adjust the balance between (i) and (ii).

Sound Heuristic Search Value Iteration for Undiscounted POMDPs with Reachability Objectives

Partially Observable Markov Decision Processes (POMDPs) are powerful models for sequential decision making under transition and observation uncertainties. This paper studies the challenging yet important problem in POMDPs known as the (indefinite-horizon) Maximal Reachability Probability Problem (MRPP), where the goal is to maximize the probability of reaching some target states. This is also a core problem in model checking with logical specifications and is naturally undiscounted (discount factor is one). Inspired by the success of point-based methods developed for discounted problems, we study their extensions to MRPP. Specifically, we focus on trial-based heuristic search value iteration techniques and present a novel algorithm that leverages the strengths of these techniques for efficient exploration of the belief space (informed search via value bounds) while addressing their drawbacks in handling loops for indefinite-horizon problems. The algorithm produces policies with two-sided bounds on optimal reachability probabilities. We prove convergence to an optimal policy from below under certain conditions. Experimental evaluations on a suite of benchmarks show that our algorithm outperforms existing methods in almost all cases in both probability guarantees and computation time.

Data-Driven Permissible Safe Control with Barrier Certificates

This paper introduces a method of identifying a maximal set of safe strategies from data for stochastic systems with unknown dynamics using barrier certificates. The first step is learning the dynamics of the system via Gaussian process (GP) regression and obtaining probabilistic errors for this estimate. Then, we develop an algorithm for constructing piecewise stochastic barrier functions to find a maximal permissible strategy set using the learned GP model, which is based on sequentially pruning the worst controls until a maximal set is identified. The permissible strategies are guaranteed to maintain probabilistic safety for the true system. This is especially important for learning-enabled systems, because a rich strategy space enables additional data collection and complex behaviors while remaining safe. Case studies on linear and nonlinear systems demonstrate that increasing the size of the dataset for learning the system grows the permissible strategy set.