Kino-PAX: Highly Parallel Kinodynamic Sampling-based Planner

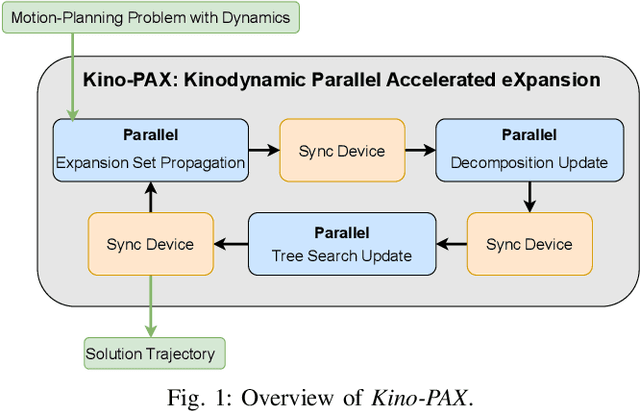
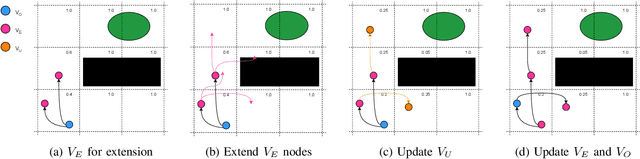
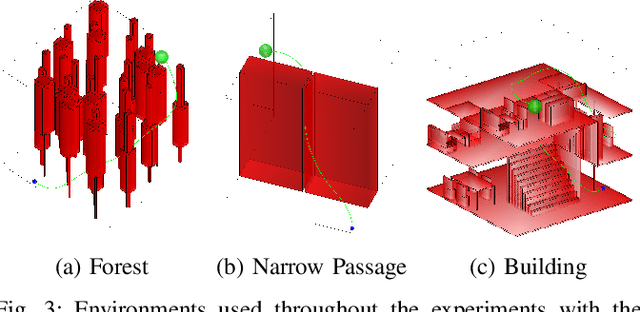
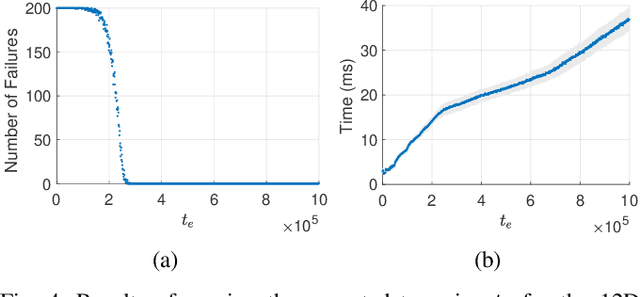
Sampling-based motion planners (SBMPs) are effective for planning with complex kinodynamic constraints in high-dimensional spaces, but they still struggle to achieve real-time performance, which is mainly due to their serial computation design. We present Kinodynamic Parallel Accelerated eXpansion (Kino-PAX), a novel highly parallel kinodynamic SBMP designed for parallel devices such as GPUs. Kino-PAX grows a tree of trajectory segments directly in parallel. Our key insight is how to decompose the iterative tree growth process into three massively parallel subroutines. Kino-PAX is designed to align with the parallel device execution hierarchies, through ensuring that threads are largely independent, share equal workloads, and take advantage of low-latency resources while minimizing high-latency data transfers and process synchronization. This design results in a very efficient GPU implementation. We prove that Kino-PAX is probabilistically complete and analyze its scalability with compute hardware improvements. Empirical evaluations demonstrate solutions in the order of 10 ms on a desktop GPU and in the order of 100 ms on an embedded GPU, representing up to 1000 times improvement compared to coarse-grained CPU parallelization of state-of-the-art sequential algorithms over a range of complex environments and systems.

Beyond Winning Strategies: Admissible and Admissible Winning Strategies for Quantitative Reachability Games

Classical reactive synthesis approaches aim to synthesize a reactive system that always satisfies a given specifications. These approaches often reduce to playing a two-player zero-sum game where the goal is to synthesize a winning strategy. However, in many pragmatic domains, such as robotics, a winning strategy does not always exist, yet it is desirable for the system to make an effort to satisfy its requirements instead of "giving up". To this end, this paper investigates the notion of admissible strategies, which formalize "doing-your-best", in quantitative reachability games. We show that, unlike the qualitative case, quantitative admissible strategies are history-dependent even for finite payoff functions, making synthesis a challenging task. In addition, we prove that admissible strategies always exist but may produce undesirable optimistic behaviors. To mitigate this, we propose admissible winning strategies, which enforce the best possible outcome while being admissible. We show that both strategies always exist but are not memoryless. We provide necessary and sufficient conditions for the existence of both strategies and propose synthesis algorithms. Finally, we illustrate the strategies on gridworld and robot manipulator domains.

Sound Heuristic Search Value Iteration for Undiscounted POMDPs with Reachability Objectives

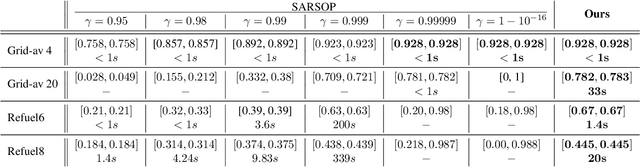
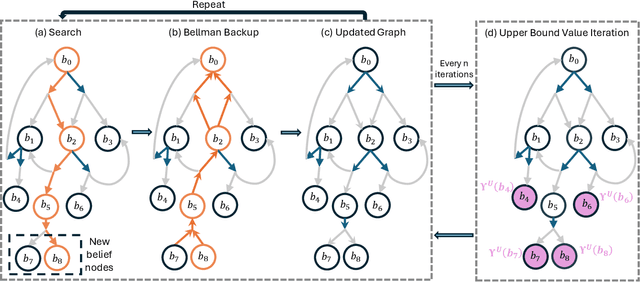
Partially Observable Markov Decision Processes (POMDPs) are powerful models for sequential decision making under transition and observation uncertainties. This paper studies the challenging yet important problem in POMDPs known as the (indefinite-horizon) Maximal Reachability Probability Problem (MRPP), where the goal is to maximize the probability of reaching some target states. This is also a core problem in model checking with logical specifications and is naturally undiscounted (discount factor is one). Inspired by the success of point-based methods developed for discounted problems, we study their extensions to MRPP. Specifically, we focus on trial-based heuristic search value iteration techniques and present a novel algorithm that leverages the strengths of these techniques for efficient exploration of the belief space (informed search via value bounds) while addressing their drawbacks in handling loops for indefinite-horizon problems. The algorithm produces policies with two-sided bounds on optimal reachability probabilities. We prove convergence to an optimal policy from below under certain conditions. Experimental evaluations on a suite of benchmarks show that our algorithm outperforms existing methods in almost all cases in both probability guarantees and computation time.

Recursively-Constrained Partially Observable Markov Decision Processes

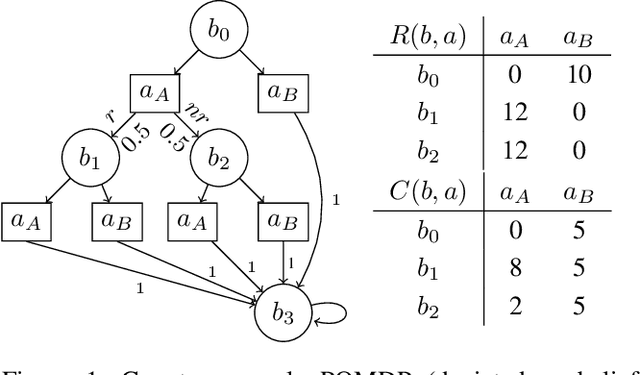
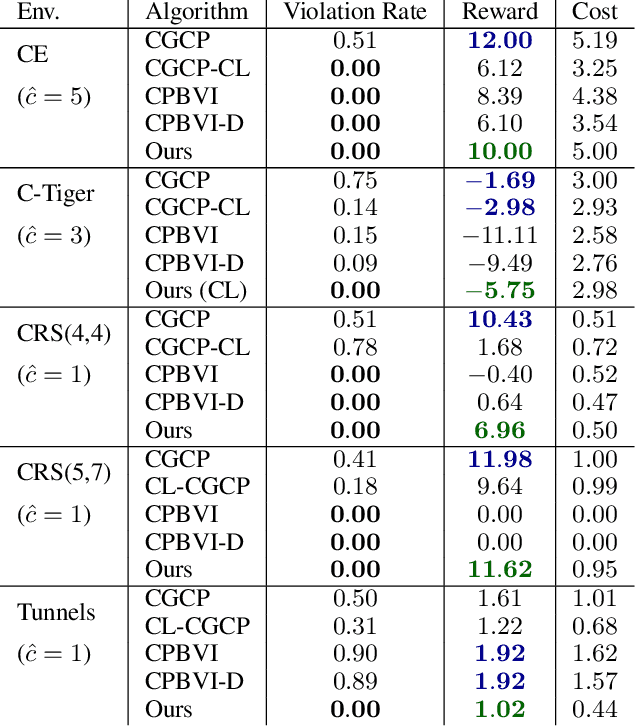
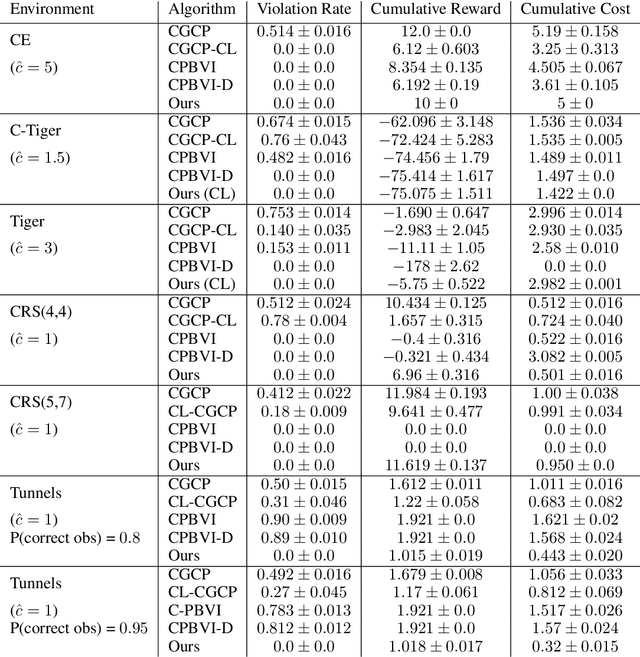
In many problems, it is desirable to optimize an objective function while imposing constraints on some other aspect of the problem. A Constrained Partially Observable Markov Decision Process (C-POMDP) allows modelling of such problems while subject to transition uncertainty and partial observability. Typically, the constraints in C-POMDPs enforce a threshold on expected cumulative costs starting from an initial state distribution. In this work, we first show that optimal C-POMDP policies may violate Bellman's principle of optimality and thus may exhibit pathological behaviors, which can be undesirable for many applications. To address this drawback, we introduce a new formulation, the Recursively-Constrained POMDP (RC-POMDP), that imposes additional history dependent cost constraints on the C-POMDP. We show that, unlike C-POMDPs, RC-POMDPs always have deterministic optimal policies, and that optimal policies obey Bellman's principle of optimality. We also present a point-based dynamic programming algorithm that synthesizes optimal policies for RC-POMDPs. In our evaluations, we show that policies for RC-POMDPs produce more desirable behavior than policies for C-POMDPs and demonstrate the efficacy of our algorithm across a set of benchmark problems.

Sampling-based Reactive Synthesis for Nondeterministic Hybrid Systems

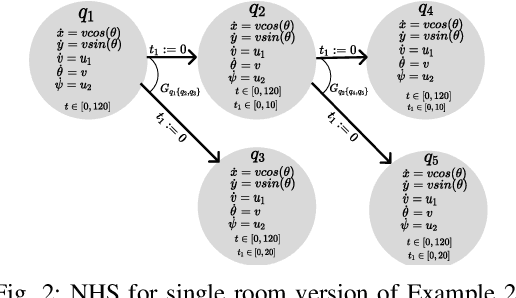
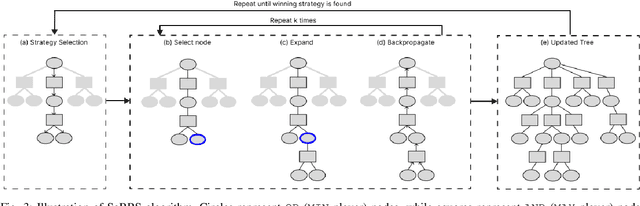
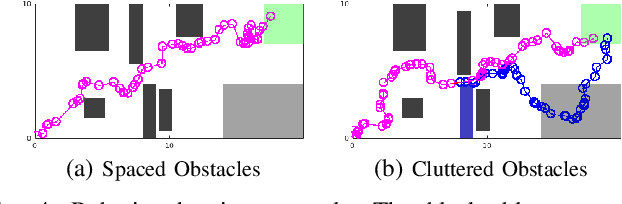
This paper introduces a sampling-based strategy synthesis algorithm for nondeterministic hybrid systems with complex continuous dynamics under temporal and reachability constraints. We view the evolution of the hybrid system as a two-player game, where the nondeterminism is an adversarial player whose objective is to prevent achieving temporal and reachability goals. The aim is to synthesize a winning strategy -- a reactive (robust) strategy that guarantees the satisfaction of the goals under all possible moves of the adversarial player. The approach is based on growing a (search) game-tree in the hybrid space by combining a sampling-based planning method with a novel bandit-based technique to select and improve on partial strategies. We provide conditions under which the algorithm is probabilistically complete, i.e., if a winning strategy exists, the algorithm will almost surely find it. The case studies and benchmark results show that the algorithm is general and consistently outperforms the state of the art.

Planning with SiMBA: Motion Planning under Uncertainty for Temporal Goals using Simplified Belief Guides

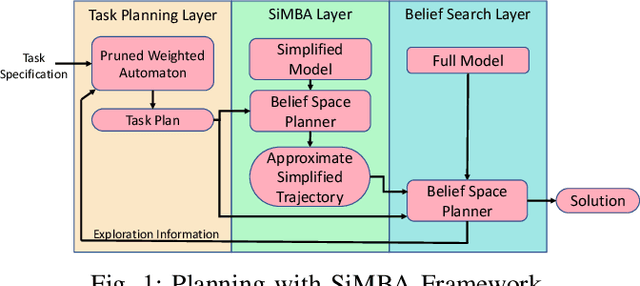
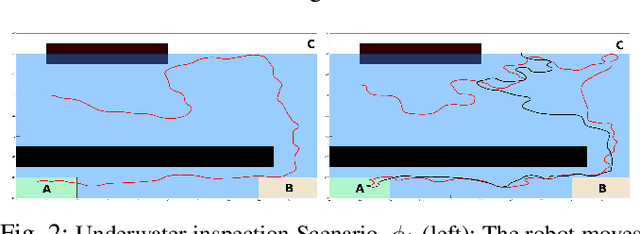
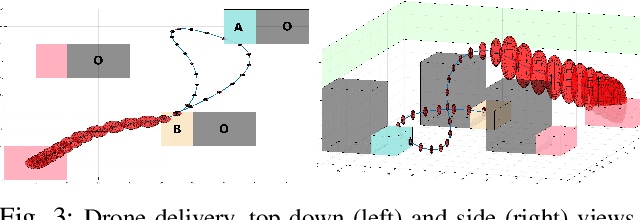
This paper presents a new multi-layered algorithm for motion planning under motion and sensing uncertainties for Linear Temporal Logic specifications. We propose a technique to guide a sampling-based search tree in the combined task and belief space using trajectories from a simplified model of the system, to make the problem computationally tractable. Our method eliminates the need to construct fine and accurate finite abstractions. We prove correctness and probabilistic completeness of our algorithm, and illustrate the benefits of our approach on several case studies. Our results show that guidance with a simplified belief space model allows for significant speed-up in planning for complex specifications.

Chance-Constrained Motion Planning with Event-Triggered Estimation

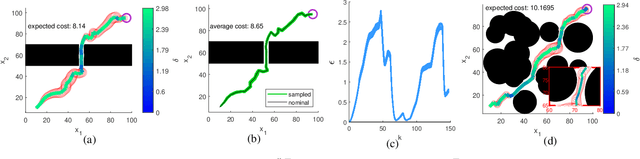
We consider the problem of autonomous navigation using limited information from a remote sensor network. Because the remote sensors are power and bandwidth limited, we use event-triggered (ET) estimation to manage communication costs. We introduce a fast and efficient sampling-based planner which computes motion plans coupled with ET communication strategies that minimize communication costs, while satisfying constraints on the probability of reaching the goal region and the point-wise probability of collision. We derive a novel method for offline propagation of the expected state distribution, and corresponding bounds on this distribution. These bounds are used to evaluate the chance constraints in the algorithm. Case studies establish the validity of our approach, demonstrating fast computation of optimal plans.

Stochastic Robustness Interval for Motion Planning with Signal Temporal Logic

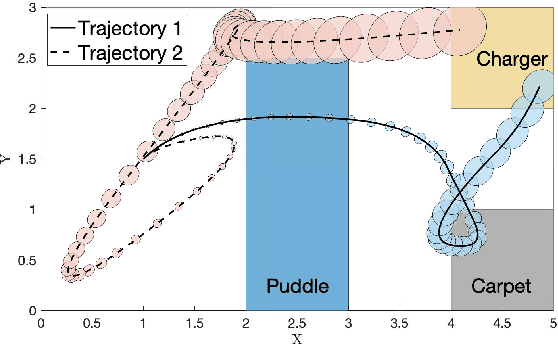
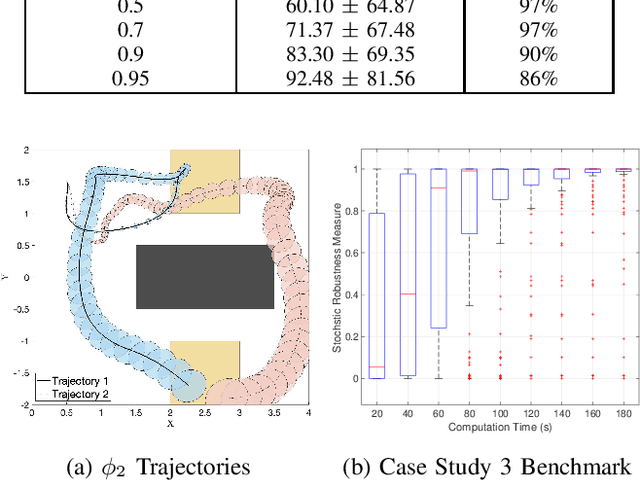
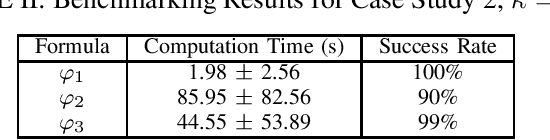
In this work, we present a novel robustness measure for continuous-time stochastic trajectories with respect to Signal Temporal Logic (STL) specifications. We show the soundness of the measure and develop a monitor for reasoning about partial trajectories. Using this monitor, we introduce an STL sampling-based motion planning algorithm for robots under uncertainty. Given a minimum robustness requirement, this algorithm finds satisfying motion plans; alternatively, the algorithm also optimizes for the measure. We prove probabilistic completeness and asymptotic optimality, and demonstrate the effectiveness of our approach on several case studies.

Automaton-Guided Control Synthesis for Signal Temporal Logic Specifications

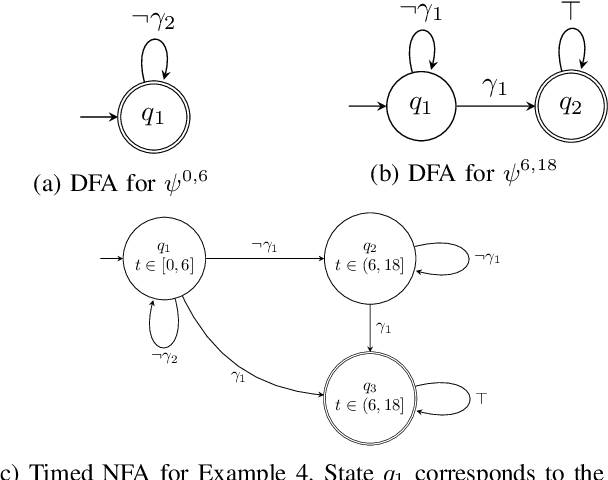
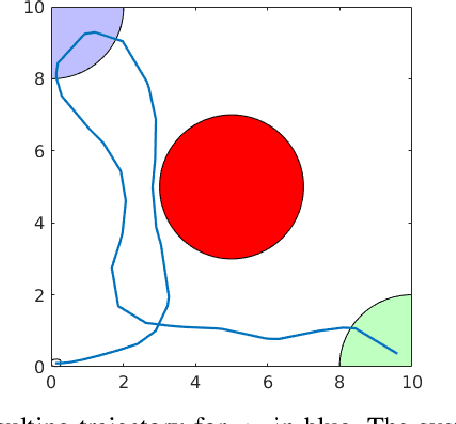
This paper presents an algorithmic framework for control synthesis of continuous dynamical systems subject to signal temporal logic (STL) specifications. We propose a novel algorithm to obtain a time-partitioned finite automaton from an STL specification, and introduce a multi-layered framework that utilizes this automaton to guide a sampling-based search tree both spatially and temporally. Our approach is able to synthesize a controller for nonlinear dynamics and polynomial predicate functions. We prove the correctness and probabilistic completeness of our algorithm, and illustrate the efficiency and efficacy of our framework on several case studies. Our results show an order of magnitude speedup over the state of the art.

Gaussian Belief Trees for Chance Constrained Asymptotically Optimal Motion Planning

In this paper, we address the problem of sampling-based motion planning under motion and measurement uncertainty with probabilistic guarantees. We generalize traditional sampling-based tree-based motion planning algorithms for deterministic systems and propose belief-$\mathcal{A}$, a framework that extends any kinodynamical tree-based planner to the belief space for linear (or linearizable) systems. We introduce appropriate sampling techniques and distance metrics for the belief space that preserve the probabilistic completeness and asymptotic optimality properties of the underlying planner. We demonstrate the efficacy of our approach for finding safe low-cost paths efficiently and asymptotically optimally in simulation, for both holonomic and non-holonomic systems.