Rao-Blackwellized POMDP Planning

Partially Observable Markov Decision Processes (POMDPs) provide a structured framework for decision-making under uncertainty, but their application requires efficient belief updates. Sequential Importance Resampling Particle Filters (SIRPF), also known as Bootstrap Particle Filters, are commonly used as belief updaters in large approximate POMDP solvers, but they face challenges such as particle deprivation and high computational costs as the system's state dimension grows. To address these issues, this study introduces Rao-Blackwellized POMDP (RB-POMDP) approximate solvers and outlines generic methods to apply Rao-Blackwellization in both belief updates and online planning. We compare the performance of SIRPF and Rao-Blackwellized Particle Filters (RBPF) in a simulated localization problem where an agent navigates toward a target in a GPS-denied environment using POMCPOW and RB-POMCPOW planners. Our results not only confirm that RBPFs maintain accurate belief approximations over time with fewer particles, but, more surprisingly, RBPFs combined with quadrature-based integration improve planning quality significantly compared to SIRPF-based planning under the same computational limits.

Sound Heuristic Search Value Iteration for Undiscounted POMDPs with Reachability Objectives

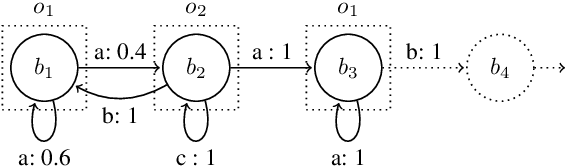
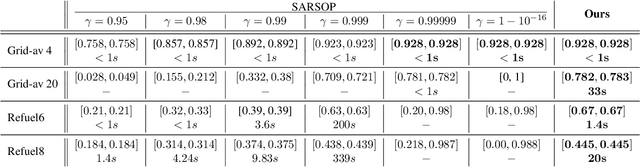
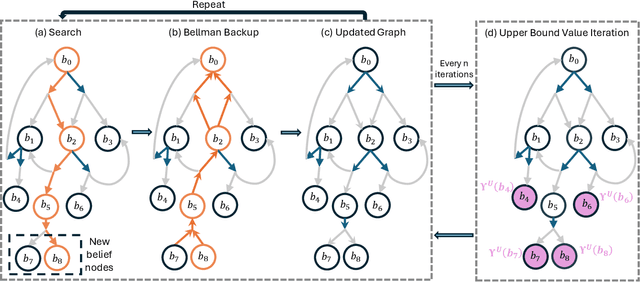
Partially Observable Markov Decision Processes (POMDPs) are powerful models for sequential decision making under transition and observation uncertainties. This paper studies the challenging yet important problem in POMDPs known as the (indefinite-horizon) Maximal Reachability Probability Problem (MRPP), where the goal is to maximize the probability of reaching some target states. This is also a core problem in model checking with logical specifications and is naturally undiscounted (discount factor is one). Inspired by the success of point-based methods developed for discounted problems, we study their extensions to MRPP. Specifically, we focus on trial-based heuristic search value iteration techniques and present a novel algorithm that leverages the strengths of these techniques for efficient exploration of the belief space (informed search via value bounds) while addressing their drawbacks in handling loops for indefinite-horizon problems. The algorithm produces policies with two-sided bounds on optimal reachability probabilities. We prove convergence to an optimal policy from below under certain conditions. Experimental evaluations on a suite of benchmarks show that our algorithm outperforms existing methods in almost all cases in both probability guarantees and computation time.

Cieran: Designing Sequential Colormaps via In-Situ Active Preference Learning

Quality colormaps can help communicate important data patterns. However, finding an aesthetically pleasing colormap that looks "just right" for a given scenario requires significant design and technical expertise. We introduce Cieran, a tool that allows any data analyst to rapidly find quality colormaps while designing charts within Jupyter Notebooks. Our system employs an active preference learning paradigm to rank expert-designed colormaps and create new ones from pairwise comparisons, allowing analysts who are novices in color design to tailor colormaps to their data context. We accomplish this by treating colormap design as a path planning problem through the CIELAB colorspace with a context-specific reward model. In an evaluation with twelve scientists, we found that Cieran effectively modeled user preferences to rank colormaps and leveraged this model to create new quality designs. Our work shows the potential of active preference learning for supporting efficient visualization design optimization.

Recursively-Constrained Partially Observable Markov Decision Processes

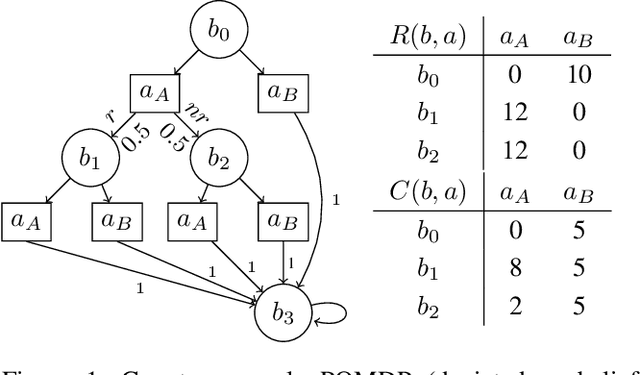
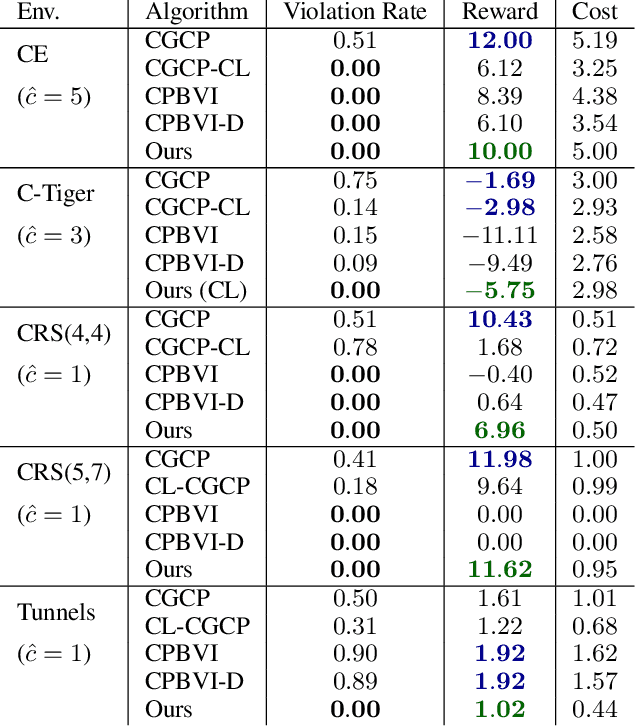
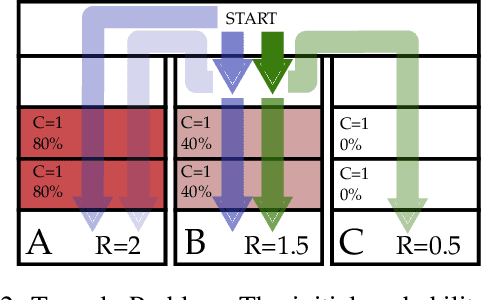
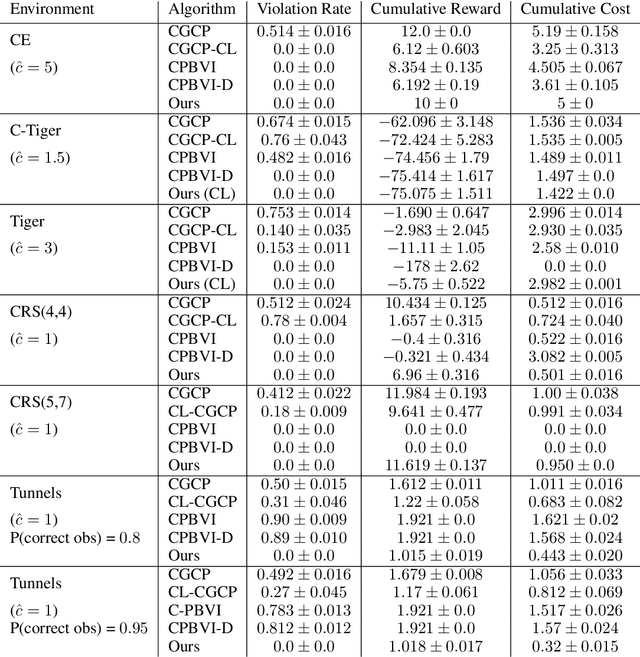
In many problems, it is desirable to optimize an objective function while imposing constraints on some other aspect of the problem. A Constrained Partially Observable Markov Decision Process (C-POMDP) allows modelling of such problems while subject to transition uncertainty and partial observability. Typically, the constraints in C-POMDPs enforce a threshold on expected cumulative costs starting from an initial state distribution. In this work, we first show that optimal C-POMDP policies may violate Bellman's principle of optimality and thus may exhibit pathological behaviors, which can be undesirable for many applications. To address this drawback, we introduce a new formulation, the Recursively-Constrained POMDP (RC-POMDP), that imposes additional history dependent cost constraints on the C-POMDP. We show that, unlike C-POMDPs, RC-POMDPs always have deterministic optimal policies, and that optimal policies obey Bellman's principle of optimality. We also present a point-based dynamic programming algorithm that synthesizes optimal policies for RC-POMDPs. In our evaluations, we show that policies for RC-POMDPs produce more desirable behavior than policies for C-POMDPs and demonstrate the efficacy of our algorithm across a set of benchmark problems.

Explanation through Reward Model Reconciliation using POMDP Tree Search

As artificial intelligence (AI) algorithms are increasingly used in mission-critical applications, promoting user-trust of these systems will be essential to their success. Ensuring users understand the models over which algorithms reason promotes user trust. This work seeks to reconcile differences between the reward model that an algorithm uses for online partially observable Markov decision (POMDP) planning and the implicit reward model assumed by a human user. Action discrepancies, differences in decisions made by an algorithm and user, are leveraged to estimate a user's objectives as expressed in weightings of a reward function.

Sampling-based Reactive Synthesis for Nondeterministic Hybrid Systems

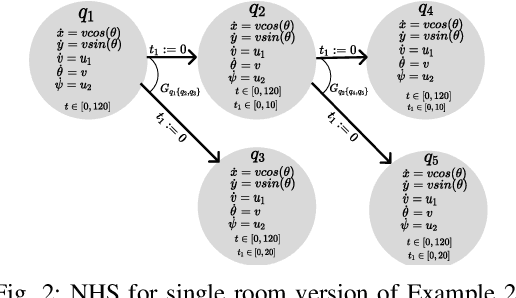
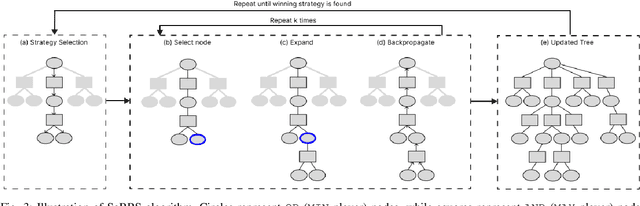
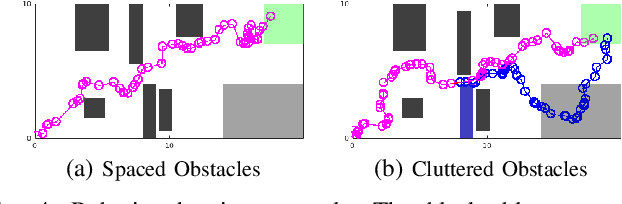
This paper introduces a sampling-based strategy synthesis algorithm for nondeterministic hybrid systems with complex continuous dynamics under temporal and reachability constraints. We view the evolution of the hybrid system as a two-player game, where the nondeterminism is an adversarial player whose objective is to prevent achieving temporal and reachability goals. The aim is to synthesize a winning strategy -- a reactive (robust) strategy that guarantees the satisfaction of the goals under all possible moves of the adversarial player. The approach is based on growing a (search) game-tree in the hybrid space by combining a sampling-based planning method with a novel bandit-based technique to select and improve on partial strategies. We provide conditions under which the algorithm is probabilistically complete, i.e., if a winning strategy exists, the algorithm will almost surely find it. The case studies and benchmark results show that the algorithm is general and consistently outperforms the state of the art.

Planning with SiMBA: Motion Planning under Uncertainty for Temporal Goals using Simplified Belief Guides

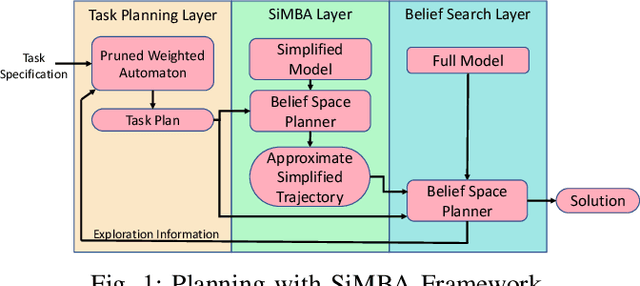
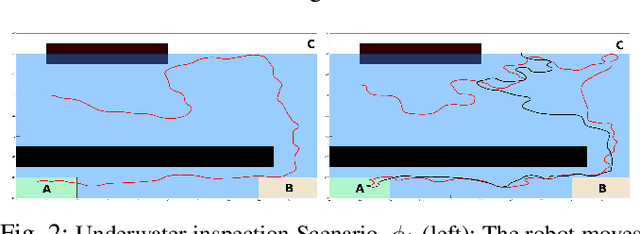
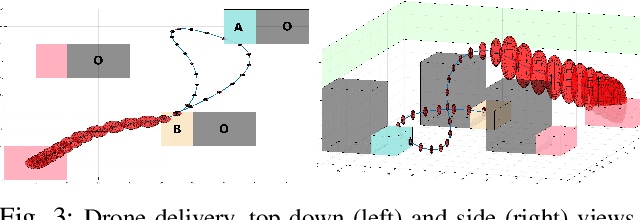
This paper presents a new multi-layered algorithm for motion planning under motion and sensing uncertainties for Linear Temporal Logic specifications. We propose a technique to guide a sampling-based search tree in the combined task and belief space using trajectories from a simplified model of the system, to make the problem computationally tractable. Our method eliminates the need to construct fine and accurate finite abstractions. We prove correctness and probabilistic completeness of our algorithm, and illustrate the benefits of our approach on several case studies. Our results show that guidance with a simplified belief space model allows for significant speed-up in planning for complex specifications.

Generalized Optimality Guarantees for Solving Continuous Observation POMDPs through Particle Belief MDP Approximation

Partially observable Markov decision processes (POMDPs) provide a flexible representation for real-world decision and control problems. However, POMDPs are notoriously difficult to solve, especially when the state and observation spaces are continuous or hybrid, which is often the case for physical systems. While recent online sampling-based POMDP algorithms that plan with observation likelihood weighting have shown practical effectiveness, a general theory bounding the approximation error of the particle filtering techniques that these algorithms use has not previously been proposed. Our main contribution is to formally justify that optimality guarantees in a finite sample particle belief MDP (PB-MDP) approximation of a POMDP/belief MDP yields optimality guarantees in the original POMDP as well. This fundamental bridge between PB-MDPs and POMDPs allows us to adapt any sampling-based MDP algorithm of choice to a POMDP by solving the corresponding particle belief MDP approximation and preserve the convergence guarantees in the POMDP. Practically, this means additionally assuming access to the observation density model, and simply swapping out the state transition generative model with a particle filtering-based model, which only increases the computational complexity by a factor of $\mathcal{O}(C)$, with $C$ the number of particles in a particle belief state. In addition to our theoretical contribution, we perform five numerical experiments on benchmark POMDPs to demonstrate that a simple MDP algorithm adapted using PB-MDP approximation, Sparse-PFT, achieves performance competitive with other leading continuous observation POMDP solvers.

Automaton-Guided Control Synthesis for Signal Temporal Logic Specifications

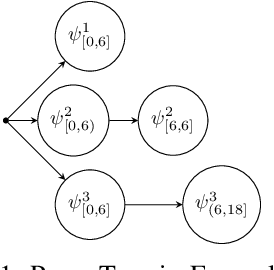
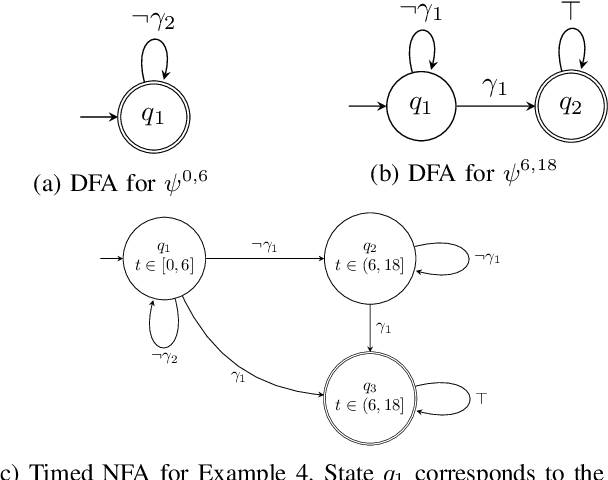
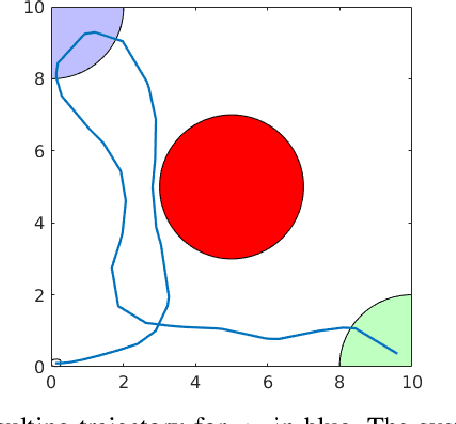
This paper presents an algorithmic framework for control synthesis of continuous dynamical systems subject to signal temporal logic (STL) specifications. We propose a novel algorithm to obtain a time-partitioned finite automaton from an STL specification, and introduce a multi-layered framework that utilizes this automaton to guide a sampling-based search tree both spatially and temporally. Our approach is able to synthesize a controller for nonlinear dynamics and polynomial predicate functions. We prove the correctness and probabilistic completeness of our algorithm, and illustrate the efficiency and efficacy of our framework on several case studies. Our results show an order of magnitude speedup over the state of the art.

Gaussian Belief Trees for Chance Constrained Asymptotically Optimal Motion Planning

In this paper, we address the problem of sampling-based motion planning under motion and measurement uncertainty with probabilistic guarantees. We generalize traditional sampling-based tree-based motion planning algorithms for deterministic systems and propose belief-$\mathcal{A}$, a framework that extends any kinodynamical tree-based planner to the belief space for linear (or linearizable) systems. We introduce appropriate sampling techniques and distance metrics for the belief space that preserve the probabilistic completeness and asymptotic optimality properties of the underlying planner. We demonstrate the efficacy of our approach for finding safe low-cost paths efficiently and asymptotically optimally in simulation, for both holonomic and non-holonomic systems.