Resolving Multiple-Dynamic Model Uncertainty in Hypothesis-Driven Belief-MDPs

When human operators of cyber-physical systems encounter surprising behavior, they often consider multiple hypotheses that might explain it. In some cases, taking information-gathering actions such as additional measurements or control inputs given to the system can help resolve uncertainty and determine the most accurate hypothesis. The task of optimizing these actions can be formulated as a belief-space Markov decision process that we call a hypothesis-driven belief MDP. Unfortunately, this problem suffers from the curse of history similar to a partially observable Markov decision process (POMDP). To plan in continuous domains, an agent needs to reason over countlessly many possible action-observation histories, each resulting in a different belief over the unknown state. The problem is exacerbated in the hypothesis-driven context because each action-observation pair spawns a different belief for each hypothesis, leading to additional branching. This paper considers the case in which each hypothesis corresponds to a different dynamic model in an underlying POMDP. We present a new belief MDP formulation that: (i) enables reasoning over multiple hypotheses, (ii) balances the goals of determining the (most likely) correct hypothesis and performing well in the underlying POMDP, and (iii) can be solved with sparse tree search.

Through the Clutter: Exploring the Impact of Complex Environments on the Legibility of Robot Motion

The environments in which the collaboration of a robot would be the most helpful to a person are frequently uncontrolled and cluttered with many objects present. Legible robot arm motion is crucial in tasks like these in order to avoid possible collisions, improve the workflow and help ensure the safety of the person. Prior work in this area, however, focuses on solutions that are tested only in uncluttered environments and there are not many results taken from cluttered environments. In this research we present a measure for clutteredness based on an entropic measure of the environment, and a novel motion planner based on potential fields. Both our measures and the planner were tested in a cluttered environment meant to represent a more typical tool sorting task for which the person would collaborate with a robot. The in-person validation study with Baxter robots shows a significant improvement in legibility of our proposed legible motion planner compared to the current state-of-the-art legible motion planner in cluttered environments. Further, the results show a significant difference in the performance of the planners in cluttered and uncluttered environments, and the need to further explore legible motion in cluttered environments. We argue that the inconsistency of our results in cluttered environments with those obtained from uncluttered environments points out several important issues with the current research performed in the area of legible motion planners.

Recursively-Constrained Partially Observable Markov Decision Processes

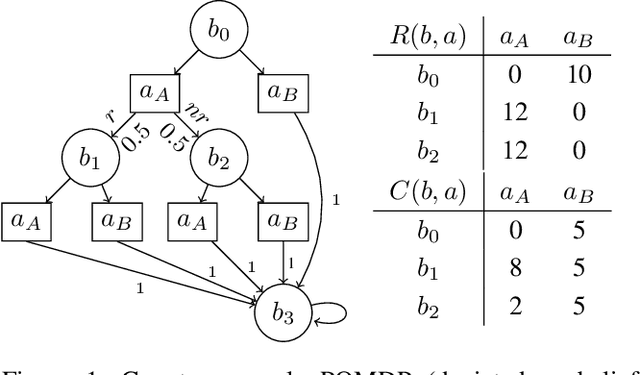
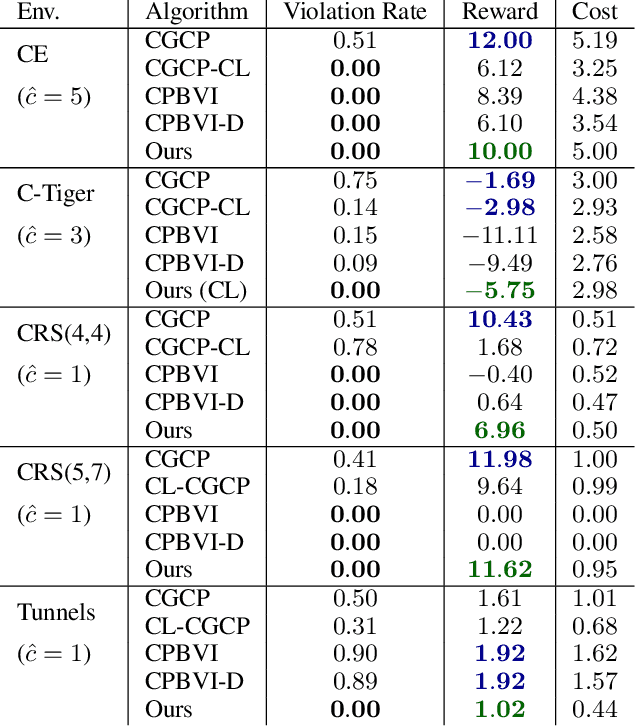
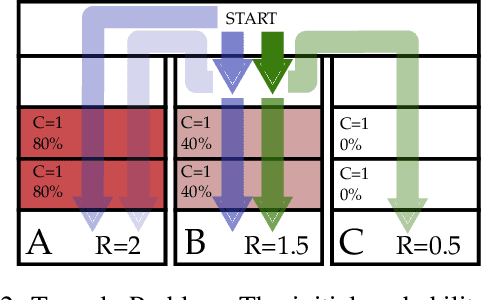
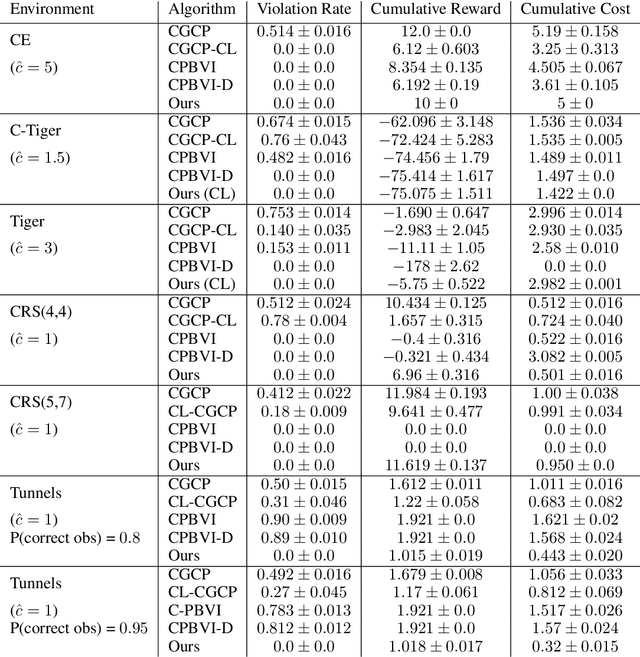
In many problems, it is desirable to optimize an objective function while imposing constraints on some other aspect of the problem. A Constrained Partially Observable Markov Decision Process (C-POMDP) allows modelling of such problems while subject to transition uncertainty and partial observability. Typically, the constraints in C-POMDPs enforce a threshold on expected cumulative costs starting from an initial state distribution. In this work, we first show that optimal C-POMDP policies may violate Bellman's principle of optimality and thus may exhibit pathological behaviors, which can be undesirable for many applications. To address this drawback, we introduce a new formulation, the Recursively-Constrained POMDP (RC-POMDP), that imposes additional history dependent cost constraints on the C-POMDP. We show that, unlike C-POMDPs, RC-POMDPs always have deterministic optimal policies, and that optimal policies obey Bellman's principle of optimality. We also present a point-based dynamic programming algorithm that synthesizes optimal policies for RC-POMDPs. In our evaluations, we show that policies for RC-POMDPs produce more desirable behavior than policies for C-POMDPs and demonstrate the efficacy of our algorithm across a set of benchmark problems.