Recursively-Constrained Partially Observable Markov Decision Processes
Paper and Code
Oct 15, 2023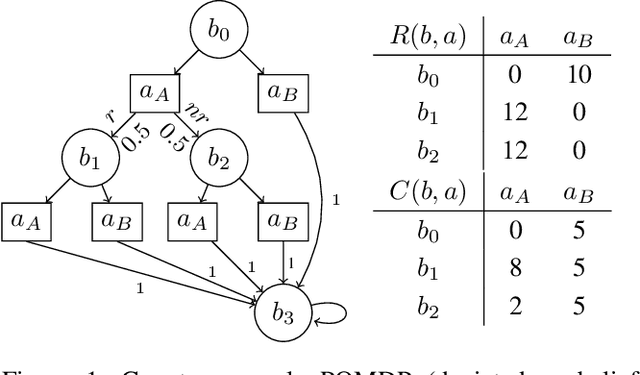
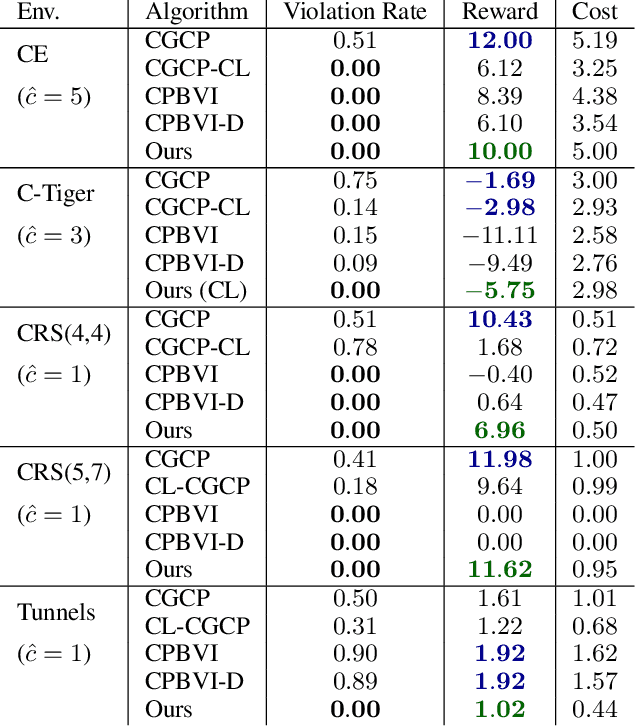
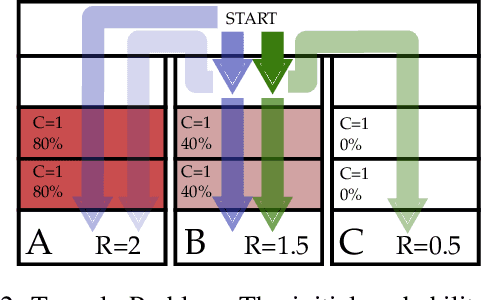
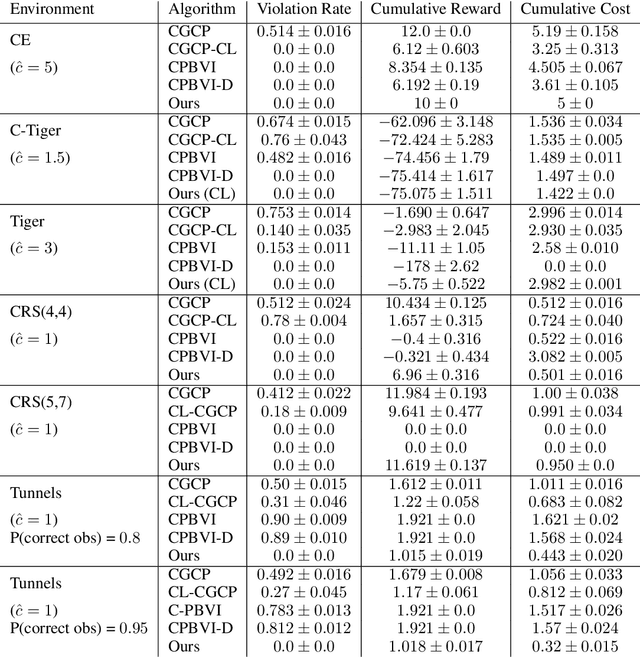
In many problems, it is desirable to optimize an objective function while imposing constraints on some other aspect of the problem. A Constrained Partially Observable Markov Decision Process (C-POMDP) allows modelling of such problems while subject to transition uncertainty and partial observability. Typically, the constraints in C-POMDPs enforce a threshold on expected cumulative costs starting from an initial state distribution. In this work, we first show that optimal C-POMDP policies may violate Bellman's principle of optimality and thus may exhibit pathological behaviors, which can be undesirable for many applications. To address this drawback, we introduce a new formulation, the Recursively-Constrained POMDP (RC-POMDP), that imposes additional history dependent cost constraints on the C-POMDP. We show that, unlike C-POMDPs, RC-POMDPs always have deterministic optimal policies, and that optimal policies obey Bellman's principle of optimality. We also present a point-based dynamic programming algorithm that synthesizes optimal policies for RC-POMDPs. In our evaluations, we show that policies for RC-POMDPs produce more desirable behavior than policies for C-POMDPs and demonstrate the efficacy of our algorithm across a set of benchmark problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge