Resolving Multiple-Dynamic Model Uncertainty in Hypothesis-Driven Belief-MDPs

When human operators of cyber-physical systems encounter surprising behavior, they often consider multiple hypotheses that might explain it. In some cases, taking information-gathering actions such as additional measurements or control inputs given to the system can help resolve uncertainty and determine the most accurate hypothesis. The task of optimizing these actions can be formulated as a belief-space Markov decision process that we call a hypothesis-driven belief MDP. Unfortunately, this problem suffers from the curse of history similar to a partially observable Markov decision process (POMDP). To plan in continuous domains, an agent needs to reason over countlessly many possible action-observation histories, each resulting in a different belief over the unknown state. The problem is exacerbated in the hypothesis-driven context because each action-observation pair spawns a different belief for each hypothesis, leading to additional branching. This paper considers the case in which each hypothesis corresponds to a different dynamic model in an underlying POMDP. We present a new belief MDP formulation that: (i) enables reasoning over multiple hypotheses, (ii) balances the goals of determining the (most likely) correct hypothesis and performing well in the underlying POMDP, and (iii) can be solved with sparse tree search.

Scalable Factor Graph-Based Heterogeneous Bayesian DDF for Dynamic Systems

Heterogeneous Bayesian decentralized data fusion captures the set of problems in which two robots must combine two probability density functions over non-equal, but overlapping sets of random variables. In the context of multi-robot dynamic systems, this enables robots to take a "divide and conquer" approach to reason and share data over complementary tasks instead of over the full joint state space. For example, in a target tracking application, this allows robots to track different subsets of targets and share data on only common targets. This paper presents a framework by which robots can each use a local factor graph to represent relevant partitions of a complex global joint probability distribution, thus allowing them to avoid reasoning over the entirety of a more complex model and saving communication as well as computation costs. From a theoretical point of view, this paper makes contributions by casting the heterogeneous decentralized fusion problem in terms of a factor graph, analyzing the challenges that arise due to dynamic filtering, and then developing a new conservative filtering algorithm that ensures statistical correctness. From a practical point of view, we show how this framework can be used to represent different multi-robot applications and then test it with simulations and hardware experiments to validate and demonstrate its statistical conservativeness, applicability, and robustness to real-world challenges.

Using Surprise Index for Competency Assessment in Autonomous Decision-Making

This paper considers the problem of evaluating an autonomous system's competency in performing a task, particularly when working in dynamic and uncertain environments. The inherent opacity of machine learning models, from the perspective of the user, often described as a `black box', poses a challenge. To overcome this, we propose using a measure called the Surprise index, which leverages available measurement data to quantify whether the dynamic system performs as expected. We show that the surprise index can be computed in closed form for dynamic systems when observed evidence in a probabilistic model if the joint distribution for that evidence follows a multivariate Gaussian marginal distribution. We then apply it to a nonlinear spacecraft maneuver problem, where actions are chosen by a reinforcement learning agent and show it can indicate how well the trajectory follows the required orbit.

Exploiting Structure for Optimal Multi-Agent Bayesian Decentralized Estimation

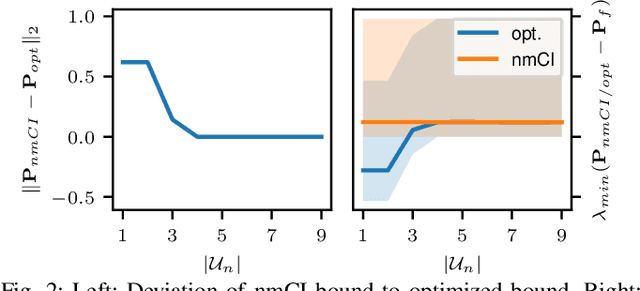
A key challenge in Bayesian decentralized data fusion is the `rumor propagation' or `double counting' phenomenon, where previously sent data circulates back to its sender. It is often addressed by approximate methods like covariance intersection (CI) which takes a weighted average of the estimates to compute the bound. The problem is that this bound is not tight, i.e. the estimate is often over-conservative. In this paper, we show that by exploiting the probabilistic independence structure in multi-agent decentralized fusion problems a tighter bound can be found using (i) an expansion to the CI algorithm that uses multiple (non-monolithic) weighting factors instead of one (monolithic) factor in the original CI and (ii) a general optimization scheme that is able to compute optimal bounds and fully exploit an arbitrary dependency structure. We compare our methods and show that on a simple problem, they converge to the same solution. We then test our new non-monolithic CI algorithm on a large-scale target tracking simulation and show that it achieves a tighter bound and a more accurate estimate compared to the original monolithic CI.

Towards Decentralized Heterogeneous Multi-Robot SLAM and Target Tracking

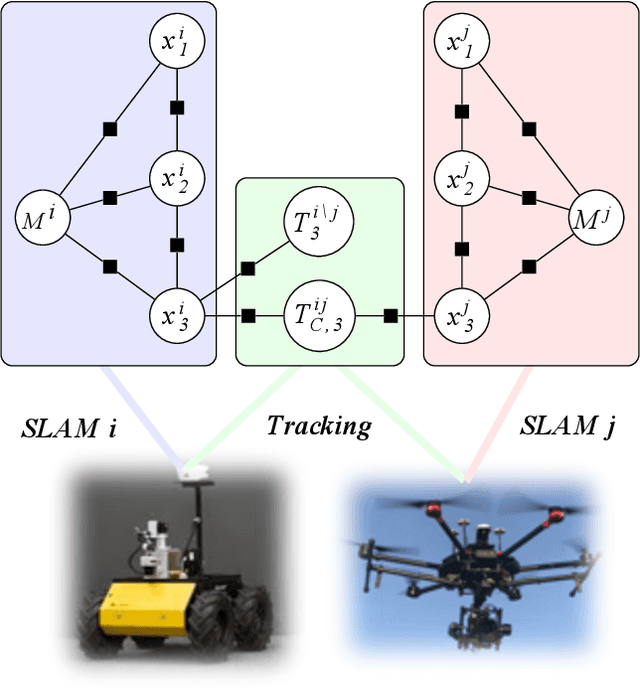
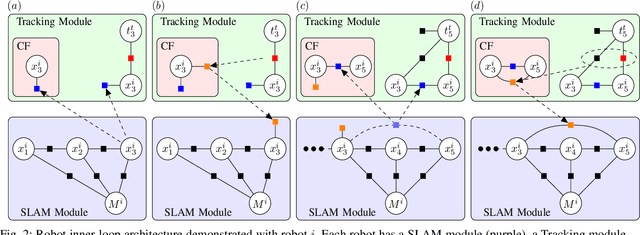
In many robotics problems, there is a significant gain in collaborative information sharing between multiple robots, for exploration, search and rescue, tracking multiple targets, or mapping large environments. One of the key implicit assumptions when solving cooperative multi-robot problems is that all robots use the same (homogeneous) underlying algorithm. However, in practice, we want to allow collaboration between robots possessing different capabilities and that therefore must rely on heterogeneous algorithms. We present a system architecture and the supporting theory, to enable collaboration in a decentralized network of robots, where each robot relies on different estimation algorithms. To develop our approach, we focus on multi-robot simultaneous localization and mapping (SLAM) with multi-target tracking. Our theoretical framework builds on our idea of exploiting the conditional independence structure inherent to many robotics applications to separate between each robot's local inference (estimation) tasks and fuse only relevant parts of their non-equal, but overlapping probability density function (pdfs). We present a new decentralized graph-based approach to the multi-robot SLAM and tracking problem. We leverage factor graphs to split between different parts of the problem for efficient data sharing between robots in the network while enabling robots to use different local sparse landmark/dense/metric-semantic SLAM algorithms.

Heterogeneous Bayesian Decentralized Data Fusion: An Empirical Study

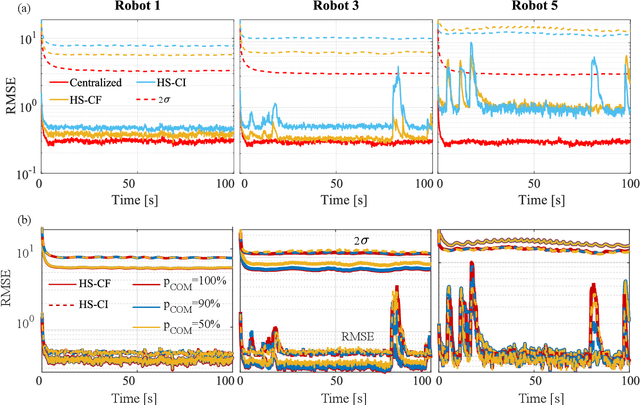
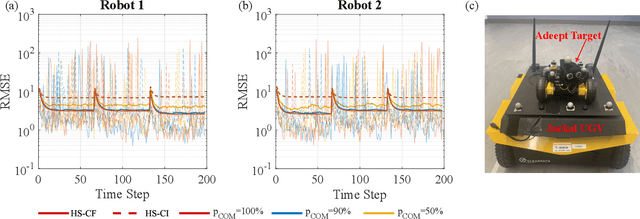
In multi-robot applications, inference over large state spaces can often be divided into smaller overlapping sub-problems that can then be collaboratively solved in parallel over `separate' subsets of states. To this end, the factor graph decentralized data fusion (FG-DDF) framework was developed to analyze and exploit conditional independence in heterogeneous Bayesian decentralized fusion problems, in which robots update and fuse pdfs over different locally overlapping random states. This allows robots to efficiently use smaller probabilistic models and sparse message passing to accurately and scalably fuse relevant local parts of a larger global joint state pdf, while accounting for data dependencies between robots. Whereas prior work required limiting assumptions about network connectivity and model linearity, this paper relaxes these to empirically explore the applicability and robustness of FG-DDF in more general settings. We develop a new heterogeneous fusion rule which generalizes the homogeneous covariance intersection algorithm, and test it in multi-robot tracking and localization scenarios with non-linear motion/observation models under communication dropout. Simulation and linear hardware experiments show that, in practice, the FG-DDF continues to provide consistent filtered estimates under these more practical operating conditions, while reducing computation and communication costs by more than 95%, thus enabling the design of scalable real-world multi-robot systems.

Conservative Filtering for Heterogeneous Decentralized Data Fusion in Dynamic Robotic Systems

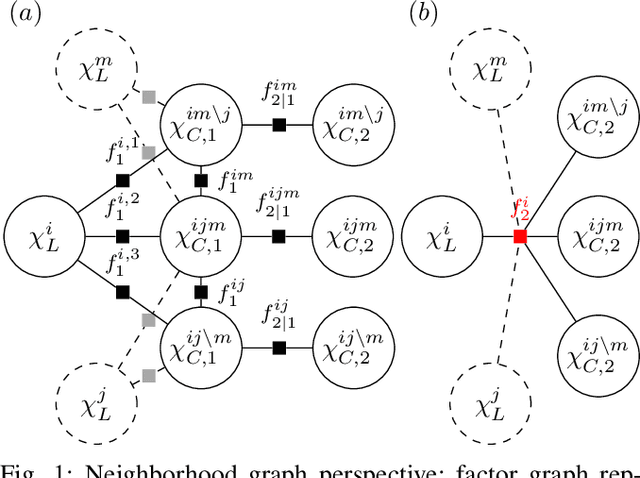
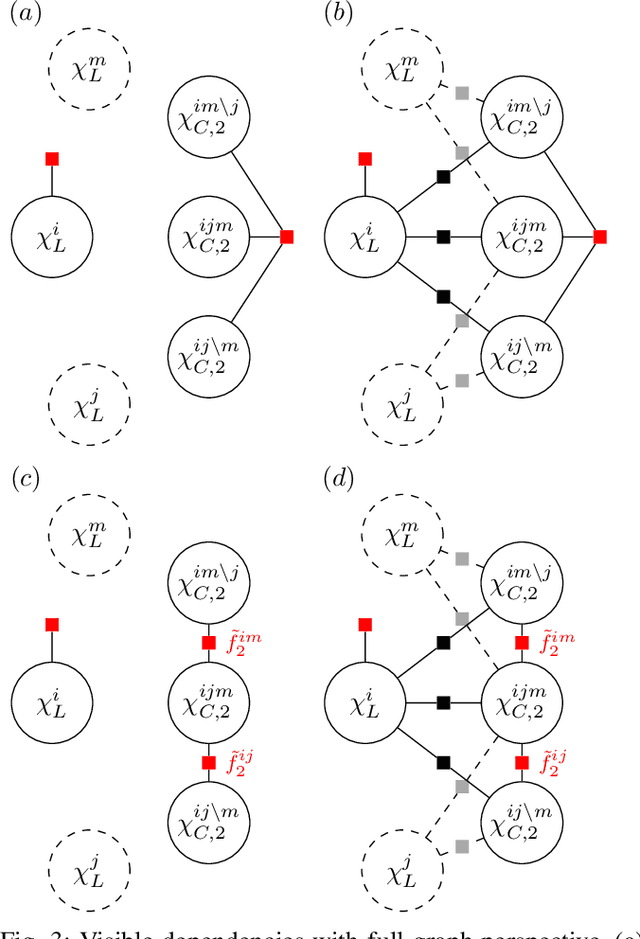
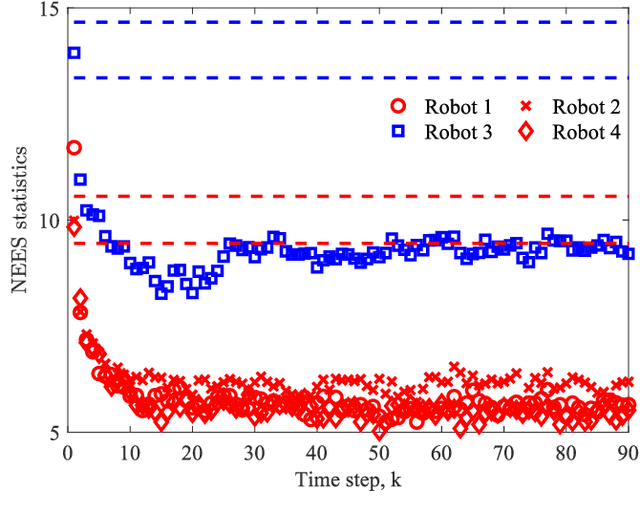
This paper presents a method for Bayesian multi-robot peer-to-peer data fusion where any pair of autonomous robots hold non-identical, but overlapping parts of a global joint probability distribution, representing real world inference tasks (e.g., mapping, tracking). It is shown that in dynamic stochastic systems, filtering, which corresponds to marginalization of past variables, results in direct and hidden dependencies between variables not mutually monitored by the robots, which might lead to an overconfident fused estimate. The paper makes both theoretical and practical contributions by providing (i) a rigorous analysis of the origin of the dependencies and and (ii) a conservative filtering algorithm for heterogeneous data fusion in dynamic systems that can be integrated with existing fusion algorithms. This work uses factor graphs as an analysis tool and an inference engine. Each robot in the network maintains a local factor graph and communicates only relevant parts of it (a sub-graph) to its neighboring robot. We discuss the applicability to various multi-robot robotic applications and demonstrate the performance using a multi-robot multi-target tracking simulation, showing that the proposed algorithm produces conservative estimates at each robot.

Factor Graphs for Heterogeneous Bayesian Decentralized Data Fusion

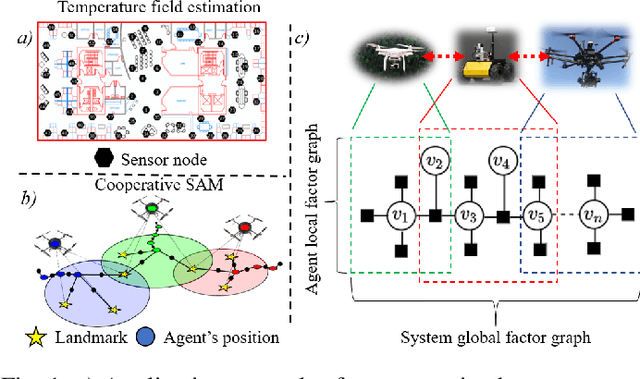
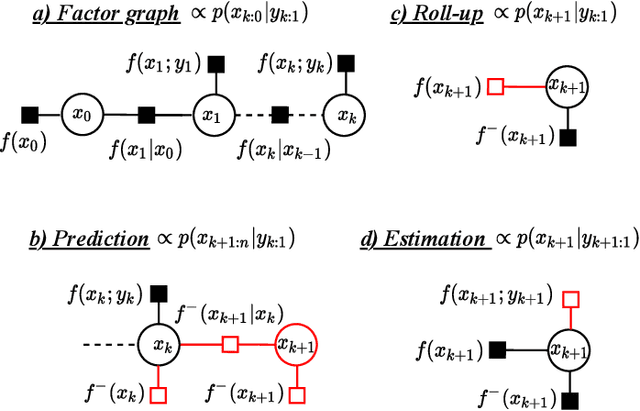
This paper explores the use of factor graphs as an inference and analysis tool for Bayesian peer-to-peer decentralized data fusion. We propose a framework by which agents can each use local factor graphs to represent relevant partitions of a complex global joint probability distribution, thus allowing them to avoid reasoning over the entirety of a more complex model and saving communication as well as computation cost. This allows heterogeneous multi-robot systems to cooperate on a variety of real world, task oriented missions, where scalability and modularity are key. To develop the initial theory and analyze the limits of this approach, we focus our attention on static linear Gaussian systems in tree-structured networks and use Channel Filters (also represented by factor graphs) to explicitly track common information. We discuss how this representation can be used to describe various multi-robot applications and to design and analyze new heterogeneous data fusion algorithms. We validate our method in simulations of a multi-agent multi-target tracking and cooperative multi-agent mapping problems, and discuss the computation and communication gains of this approach.

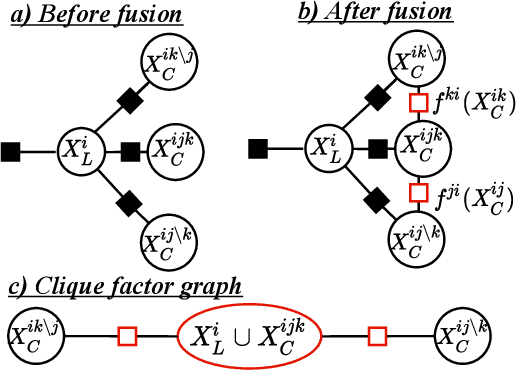
Exact and Approximate Heterogeneous Bayesian Decentralized Data Fusion

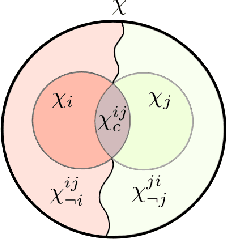
In Bayesian peer-to-peer decentralized data fusion for static and dynamic systems, the underlying estimated or communicated distributions are frequently assumed to be homogeneous between agents. This requires each agent to process and communicate the full global joint distribution, and thus leads to high computation and communication costs irrespective of relevancy to specific local objectives. This work considers a family of heterogeneous decentralized fusion problems, where we consider the set of problems in which either the communicated or the estimated distributions describe different, but overlapping, states of interest that are subsets of a larger full global joint state. We exploit the conditional independence structure of such problems and provide a rigorous derivation for a family of exact and approximate heterogeneous conditionally factorized channel filter methods. We further extend existing methods for approximate conservative filtering and decentralized fusion in heterogeneous dynamic problems. Numerical examples show more than 99.5% potential communication reduction for heterogeneous channel filter fusion, and a multi-target tracking simulation shows that these methods provide consistent estimates.