Operator Splitting Covariance Steering for Safe Stochastic Nonlinear Control

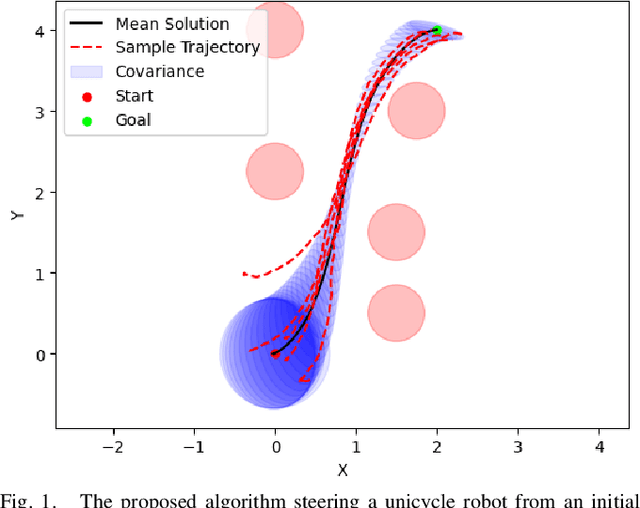
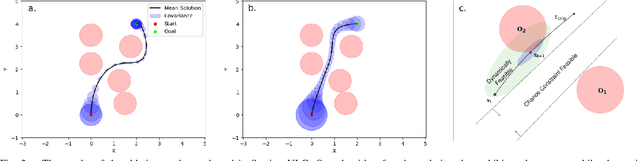
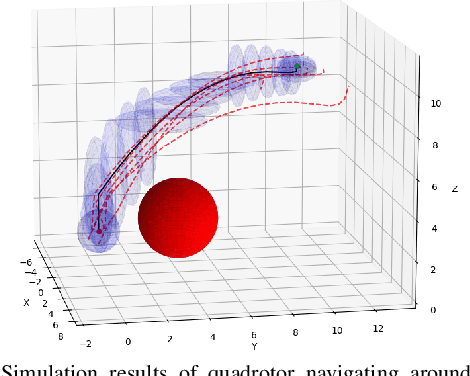
Most robotics applications are typically accompanied with safety restrictions that need to be satisfied with a high degree of confidence even in environments under uncertainty. Controlling the state distribution of a system and enforcing such specifications as distribution constraints is a promising approach for meeting such requirements. In this direction, covariance steering (CS) is an increasingly popular stochastic optimal control (SOC) framework for designing safe controllers via explicit constraints on the system covariance. Nevertheless, a major challenge in applying CS methods to systems with the nonlinear dynamics and chance constraints common in robotics is that the approximations needed are conservative and highly sensitive to the point of approximation. This can cause sequential convex programming methods to converge to poor local minima or incorrectly report problems as infeasible due to shifting constraints. This paper presents a novel algorithm for solving chance-constrained nonlinear CS problems that directly addresses this challenge. Specifically, we propose an operator-splitting approach that temporarily separates the main problem into subproblems that can be solved in parallel. The benefit of this relaxation lies in the fact that it does not require all iterates to satisfy all constraints simultaneously prior to convergence, thus enhancing the exploration capabilities of the algorithm for finding better solutions. Simulation results verify the ability of the proposed method to find higher quality solutions under stricter safety constraints than standard methods on a variety of robotic systems. Finally, the applicability of the algorithm on real systems is confirmed through hardware demonstrations.

Using Surprise Index for Competency Assessment in Autonomous Decision-Making

This paper considers the problem of evaluating an autonomous system's competency in performing a task, particularly when working in dynamic and uncertain environments. The inherent opacity of machine learning models, from the perspective of the user, often described as a `black box', poses a challenge. To overcome this, we propose using a measure called the Surprise index, which leverages available measurement data to quantify whether the dynamic system performs as expected. We show that the surprise index can be computed in closed form for dynamic systems when observed evidence in a probabilistic model if the joint distribution for that evidence follows a multivariate Gaussian marginal distribution. We then apply it to a nonlinear spacecraft maneuver problem, where actions are chosen by a reinforcement learning agent and show it can indicate how well the trajectory follows the required orbit.

Safety Guarantees for Neural Network Dynamic Systems via Stochastic Barrier Functions

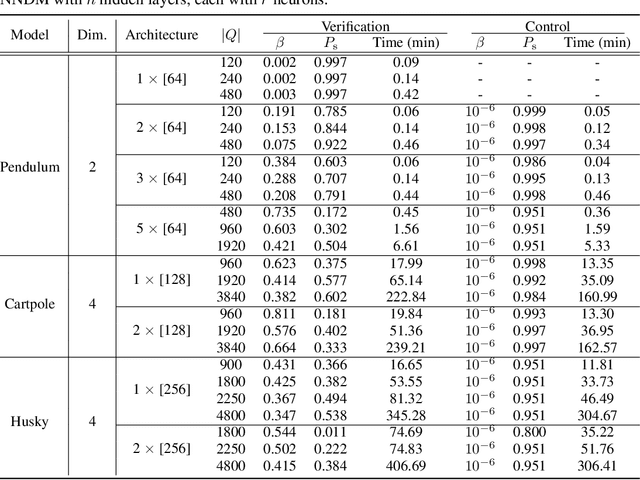
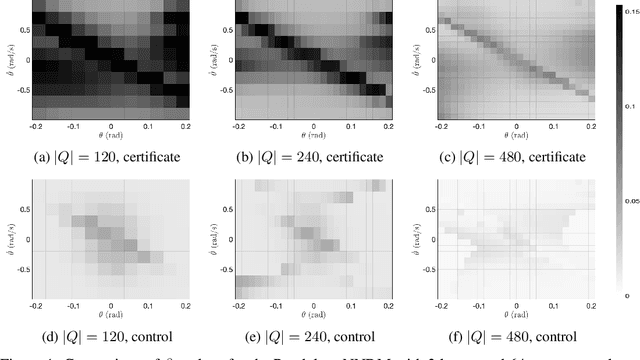
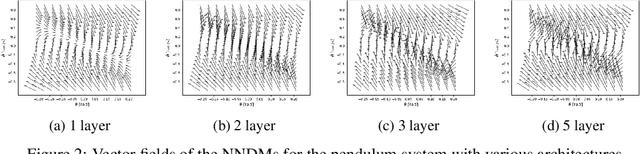
Neural Networks (NNs) have been successfully employed to represent the state evolution of complex dynamical systems. Such models, referred to as NN dynamic models (NNDMs), use iterative noisy predictions of NN to estimate a distribution of system trajectories over time. Despite their accuracy, safety analysis of NNDMs is known to be a challenging problem and remains largely unexplored. To address this issue, in this paper, we introduce a method of providing safety guarantees for NNDMs. Our approach is based on stochastic barrier functions, whose relation with safety are analogous to that of Lyapunov functions with stability. We first show a method of synthesizing stochastic barrier functions for NNDMs via a convex optimization problem, which in turn provides a lower bound on the system's safety probability. A key step in our method is the employment of the recent convex approximation results for NNs to find piece-wise linear bounds, which allow the formulation of the barrier function synthesis problem as a sum-of-squares optimization program. If the obtained safety probability is above the desired threshold, the system is certified. Otherwise, we introduce a method of generating controls for the system that robustly maximizes the safety probability in a minimally-invasive manner. We exploit the convexity property of the barrier function to formulate the optimal control synthesis problem as a linear program. Experimental results illustrate the efficacy of the method. Namely, they show that the method can scale to multi-dimensional NNDMs with multiple layers and hundreds of neurons per layer, and that the controller can significantly improve the safety probability.