Optimal Control Theoretic Neural Optimizer: From Backpropagation to Dynamic Programming

Optimization of deep neural networks (DNNs) has been a driving force in the advancement of modern machine learning and artificial intelligence. With DNNs characterized by a prolonged sequence of nonlinear propagation, determining their optimal parameters given an objective naturally fits within the framework of Optimal Control Programming. Such an interpretation of DNNs as dynamical systems has proven crucial in offering a theoretical foundation for principled analysis from numerical equations to physics. In parallel to these theoretical pursuits, this paper focuses on an algorithmic perspective. Our motivated observation is the striking algorithmic resemblance between the Backpropagation algorithm for computing gradients in DNNs and the optimality conditions for dynamical systems, expressed through another backward process known as dynamic programming. Consolidating this connection, where Backpropagation admits a variational structure, solving an approximate dynamic programming up to the first-order expansion leads to a new class of optimization methods exploring higher-order expansions of the Bellman equation. The resulting optimizer, termed Optimal Control Theoretic Neural Optimizer (OCNOpt), enables rich algorithmic opportunities, including layer-wise feedback policies, game-theoretic applications, and higher-order training of continuous-time models such as Neural ODEs. Extensive experiments demonstrate that OCNOpt improves upon existing methods in robustness and efficiency while maintaining manageable computational complexity, paving new avenues for principled algorithmic design grounded in dynamical systems and optimal control theory.

Momentum Multi-Marginal Schrödinger Bridge Matching

Understanding complex systems by inferring trajectories from sparse sample snapshots is a fundamental challenge in a wide range of domains, e.g., single-cell biology, meteorology, and economics. Despite advancements in Bridge and Flow matching frameworks, current methodologies rely on pairwise interpolation between adjacent snapshots. This hinders their ability to capture long-range temporal dependencies and potentially affects the coherence of the inferred trajectories. To address these issues, we introduce \textbf{Momentum Multi-Marginal Schr\"odinger Bridge Matching (3MSBM)}, a novel matching framework that learns smooth measure-valued splines for stochastic systems that satisfy multiple positional constraints. This is achieved by lifting the dynamics to phase space and generalizing stochastic bridges to be conditioned on several points, forming a multi-marginal conditional stochastic optimal control problem. The underlying dynamics are then learned by minimizing a variational objective, having fixed the path induced by the multi-marginal conditional bridge. As a matching approach, 3MSBM learns transport maps that preserve intermediate marginals throughout training, significantly improving convergence and scalability. Extensive experimentation in a series of real-world applications validates the superior performance of 3MSBM compared to existing methods in capturing complex dynamics with temporal dependencies, opening new avenues for training matching frameworks in multi-marginal settings.

Nearly Optimal Nonlinear Safe Control with BaS-SDRE

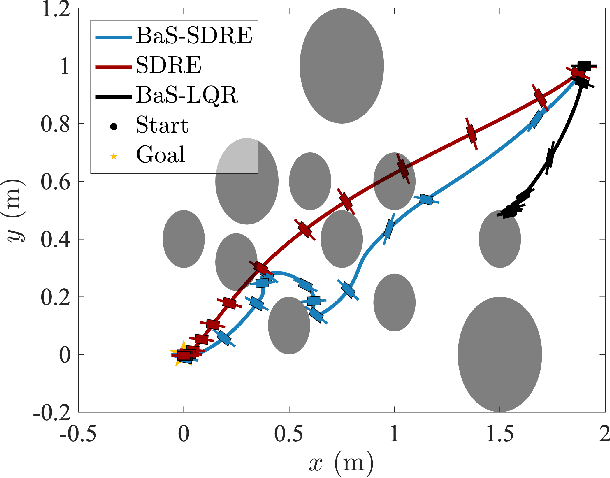
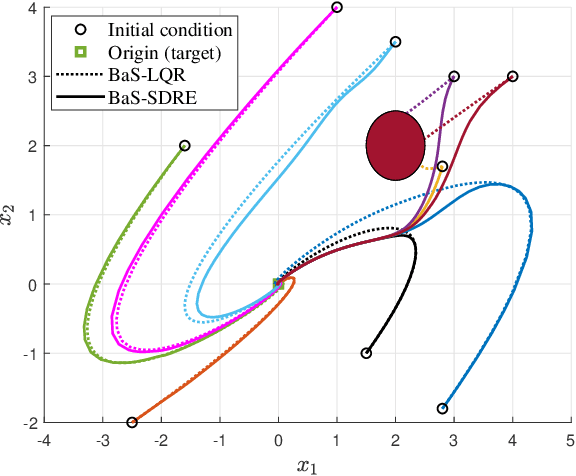
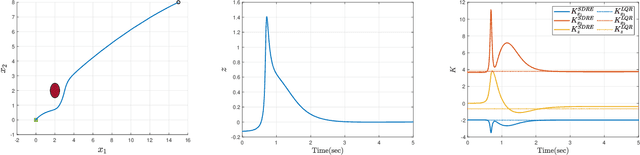
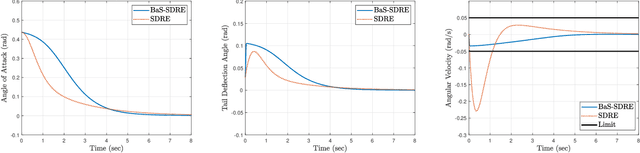
The State-Dependent Riccati Equation (SDRE) approach has emerged as a systematic and effective means of designing nearly optimal nonlinear controllers. The Barrier States (BaS) embedding methodology was developed recently for safe multi-objective controls in which the safety condition is manifested as a state to be controlled along with other states of the system. The overall system, termed the safety embedded system, is highly nonlinear even if the original system is linear. This paper develops a nonlinear nearly optimal safe feedback control technique by combining the two strategies effectively. First, the BaS is derived in an extended linearization formulation to be subsequently used to form an extended safety embedded system. A new optimal control problem is formed thereafter, which is used to construct a safety embedded State-Dependent Riccati Equation, termed BaS-SDRE, whose solution approximates the solution of the optimal control problem's associated Hamilton-Jacobi-Bellman (HJB) equation. The BaS-SDRE is then solved online to synthesize the nearly optimal safe control. The proposed technique's efficacy is demonstrated on an unstable, constrained linear system that shows how the synthesized control reacts to nonlinearities near the unsafe region, a nonlinear flight control system with limited path angular velocity that exists due to structural and dynamic concerns, and a planar quadrotor system that navigates safely in a crowded environment.

Nonlinear Robust Optimization for Planning and Control

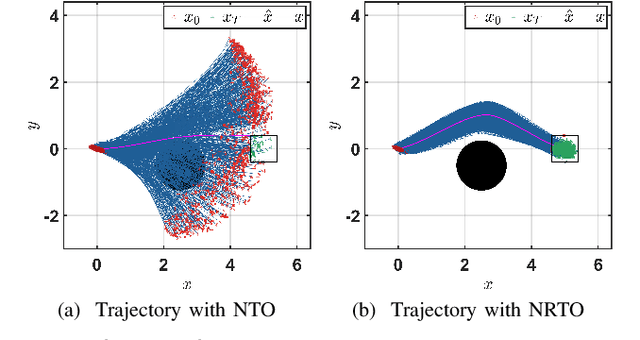
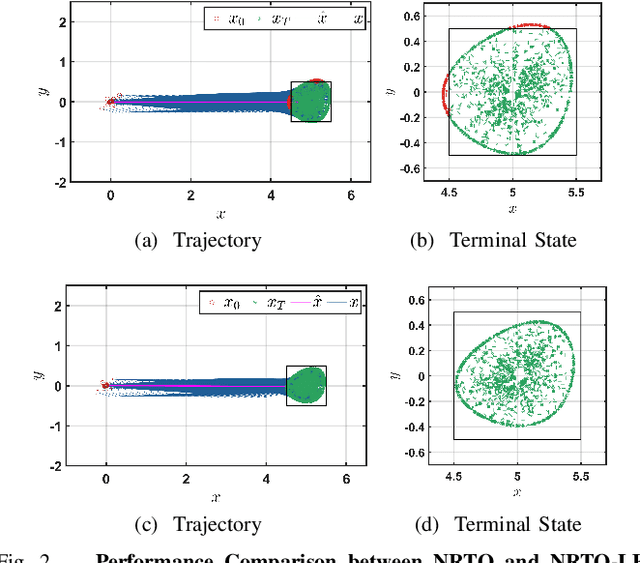
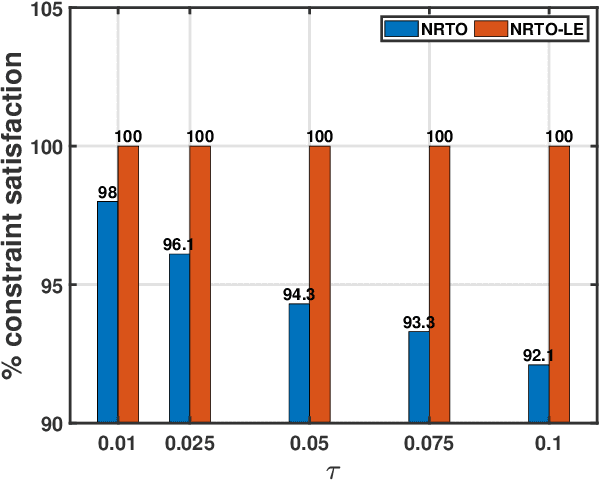
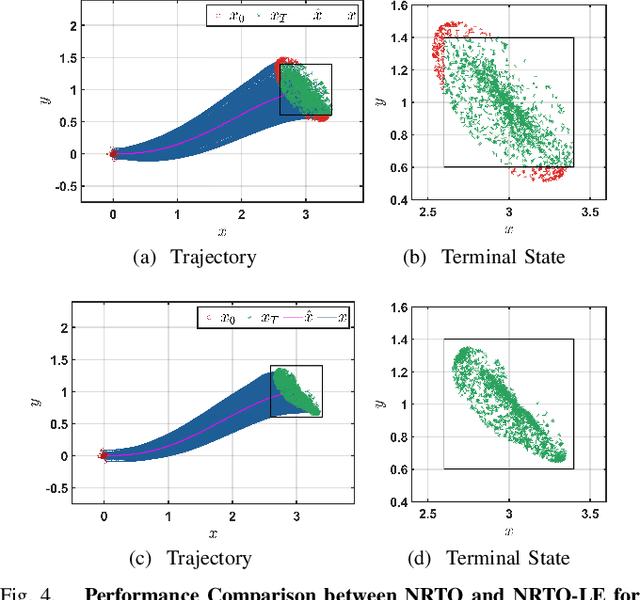
This paper presents a novel robust trajectory optimization method for constrained nonlinear dynamical systems subject to unknown bounded disturbances. In particular, we seek optimal control policies that remain robustly feasible with respect to all possible realizations of the disturbances within prescribed uncertainty sets. To address this problem, we introduce a bi-level optimization algorithm. The outer level employs a trust-region successive convexification approach which relies on linearizing the nonlinear dynamics and robust constraints. The inner level involves solving the resulting linearized robust optimization problems, for which we derive tractable convex reformulations and present an Augmented Lagrangian method for efficiently solving them. To further enhance the robustness of our methodology on nonlinear systems, we also illustrate that potential linearization errors can be effectively modeled as unknown disturbances as well. Simulation results verify the applicability of our approach in controlling nonlinear systems in a robust manner under unknown disturbances. The promise of effectively handling approximation errors in such successive linearization schemes from a robust optimization perspective is also highlighted.

Deep Generalized Schrödinger Bridges: From Image Generation to Solving Mean-Field Games

Generalized Schr\"odinger Bridges (GSBs) are a fundamental mathematical framework used to analyze the most likely particle evolution based on the principle of least action including kinetic and potential energy. In parallel to their well-established presence in the theoretical realms of quantum mechanics and optimal transport, this paper focuses on an algorithmic perspective, aiming to enhance practical usage. Our motivated observation is that transportation problems with the optimality structures delineated by GSBs are pervasive across various scientific domains, such as generative modeling in machine learning, mean-field games in stochastic control, and more. Exploring the intrinsic connection between the mathematical modeling of GSBs and the modern algorithmic characterization therefore presents a crucial, yet untapped, avenue. In this paper, we reinterpret GSBs as probabilistic models and demonstrate that, with a delicate mathematical tool known as the nonlinear Feynman-Kac lemma, rich algorithmic concepts, such as likelihoods, variational gaps, and temporal differences, emerge naturally from the optimality structures of GSBs. The resulting computational framework, driven by deep learning and neural networks, operates in a fully continuous state space (i.e., mesh-free) and satisfies distribution constraints, setting it apart from prior numerical solvers relying on spatial discretization or constraint relaxation. We demonstrate the efficacy of our method in generative modeling and mean-field games, highlighting its transformative applications at the intersection of mathematical modeling, stochastic process, control, and machine learning.

Deep Distributed Optimization for Large-Scale Quadratic Programming

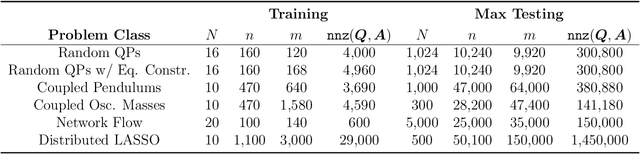
Quadratic programming (QP) forms a crucial foundation in optimization, encompassing a broad spectrum of domains and serving as the basis for more advanced algorithms. Consequently, as the scale and complexity of modern applications continue to grow, the development of efficient and reliable QP algorithms is becoming increasingly vital. In this context, this paper introduces a novel deep learning-aided distributed optimization architecture designed for tackling large-scale QP problems. First, we combine the state-of-the-art Operator Splitting QP (OSQP) method with a consensus approach to derive DistributedQP, a new method tailored for network-structured problems, with convergence guarantees to optimality. Subsequently, we unfold this optimizer into a deep learning framework, leading to DeepDistributedQP, which leverages learned policies to accelerate reaching to desired accuracy within a restricted amount of iterations. Our approach is also theoretically grounded through Probably Approximately Correct (PAC)-Bayes theory, providing generalization bounds on the expected optimality gap for unseen problems. The proposed framework, as well as its centralized version DeepQP, significantly outperform their standard optimization counterparts on a variety of tasks such as randomly generated problems, optimal control, linear regression, transportation networks and others. Notably, DeepDistributedQP demonstrates strong generalization by training on small problems and scaling to solve much larger ones (up to 50K variables and 150K constraints) using the same policy. Moreover, it achieves orders-of-magnitude improvements in wall-clock time compared to OSQP. The certifiable performance guarantees of our approach are also demonstrated, ensuring higher-quality solutions over traditional optimizers.

Dynamics Modeling using Visual Terrain Features for High-Speed Autonomous Off-Road Driving

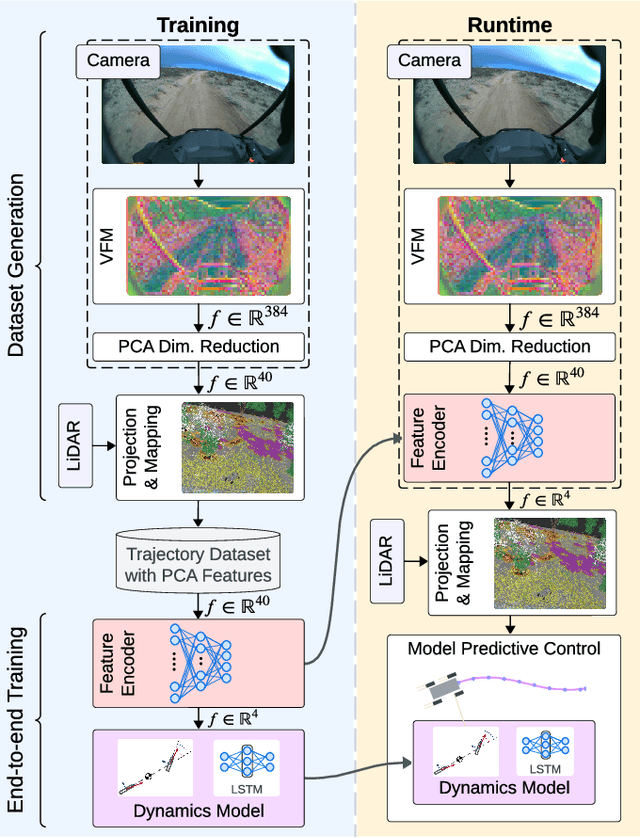
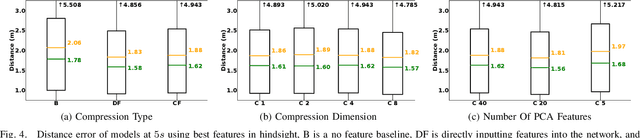
Rapid autonomous traversal of unstructured terrain is essential for scenarios such as disaster response, search and rescue, or planetary exploration. As a vehicle navigates at the limit of its capabilities over extreme terrain, its dynamics can change suddenly and dramatically. For example, high-speed and varying terrain can affect parameters such as traction, tire slip, and rolling resistance. To achieve effective planning in such environments, it is crucial to have a dynamics model that can accurately anticipate these conditions. In this work, we present a hybrid model that predicts the changing dynamics induced by the terrain as a function of visual inputs. We leverage a pre-trained visual foundation model (VFM) DINOv2, which provides rich features that encode fine-grained semantic information. To use this dynamics model for planning, we propose an end-to-end training architecture for a projection distance independent feature encoder that compresses the information from the VFM, enabling the creation of a lightweight map of the environment at runtime. We validate our architecture on an extensive dataset (hundreds of kilometers of aggressive off-road driving) collected across multiple locations as part of the DARPA Robotic Autonomy in Complex Environments with Resiliency (RACER) program. https://www.youtube.com/watch?v=dycTXxEosMk

Operator Splitting Covariance Steering for Safe Stochastic Nonlinear Control

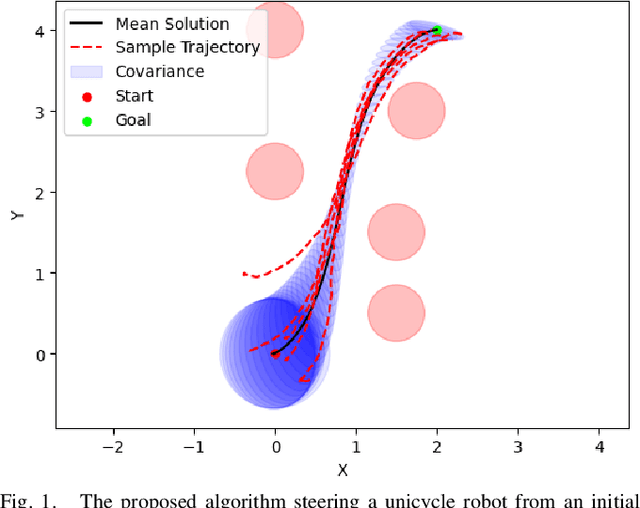
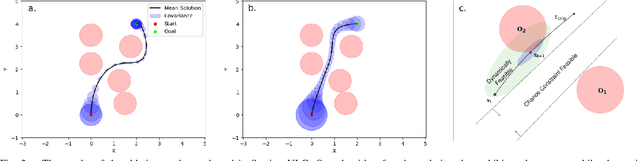
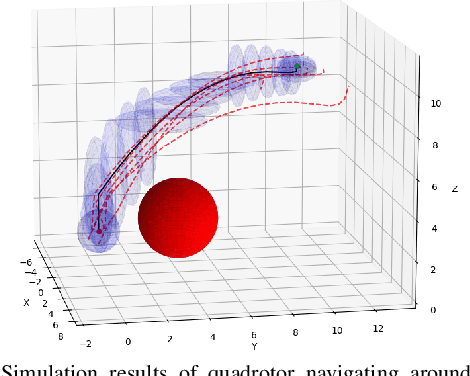
Most robotics applications are typically accompanied with safety restrictions that need to be satisfied with a high degree of confidence even in environments under uncertainty. Controlling the state distribution of a system and enforcing such specifications as distribution constraints is a promising approach for meeting such requirements. In this direction, covariance steering (CS) is an increasingly popular stochastic optimal control (SOC) framework for designing safe controllers via explicit constraints on the system covariance. Nevertheless, a major challenge in applying CS methods to systems with the nonlinear dynamics and chance constraints common in robotics is that the approximations needed are conservative and highly sensitive to the point of approximation. This can cause sequential convex programming methods to converge to poor local minima or incorrectly report problems as infeasible due to shifting constraints. This paper presents a novel algorithm for solving chance-constrained nonlinear CS problems that directly addresses this challenge. Specifically, we propose an operator-splitting approach that temporarily separates the main problem into subproblems that can be solved in parallel. The benefit of this relaxation lies in the fact that it does not require all iterates to satisfy all constraints simultaneously prior to convergence, thus enhancing the exploration capabilities of the algorithm for finding better solutions. Simulation results verify the ability of the proposed method to find higher quality solutions under stricter safety constraints than standard methods on a variety of robotic systems. Finally, the applicability of the algorithm on real systems is confirmed through hardware demonstrations.

Feedback Schrödinger Bridge Matching

Recent advancements in diffusion bridges for distribution transport problems have heavily relied on matching frameworks, yet existing methods often face a trade-off between scalability and access to optimal pairings during training. Fully unsupervised methods make minimal assumptions but incur high computational costs, limiting their practicality. On the other hand, imposing full supervision of the matching process with optimal pairings improves scalability, however, it can be infeasible in many applications. To strike a balance between scalability and minimal supervision, we introduce Feedback Schr\"odinger Bridge Matching (FSBM), a novel semi-supervised matching framework that incorporates a small portion (less than 8% of the entire dataset) of pre-aligned pairs as state feedback to guide the transport map of non coupled samples, thereby significantly improving efficiency. This is achieved by formulating a static Entropic Optimal Transport (EOT) problem with an additional term capturing the semi-supervised guidance. The generalized EOT objective is then recast into a dynamic formulation to leverage the scalability of matching frameworks. Extensive experiments demonstrate that FSBM accelerates training and enhances generalization by leveraging coupled pairs guidance, opening new avenues for training matching frameworks with partially aligned datasets.

MPPI-Generic: A CUDA Library for Stochastic Optimization

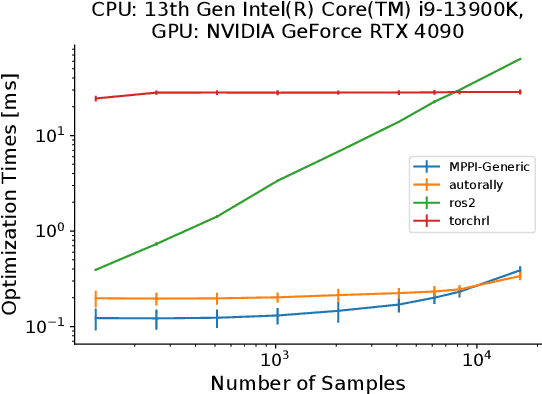
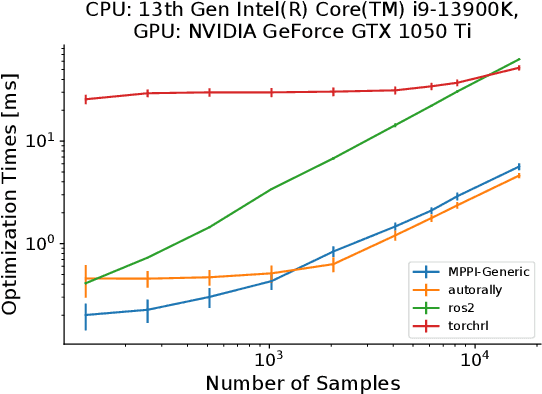
This paper introduces a new C++/CUDA library for GPU-accelerated stochastic optimization called MPPI-Generic. It provides implementations of Model Predictive Path Integral control, Tube-Model Predictive Path Integral Control, and Robust Model Predictive Path Integral Control, and allows for these algorithms to be used across many pre-existing dynamics models and cost functions. Furthermore, researchers can create their own dynamics models or cost functions following our API definitions without needing to change the actual Model Predictive Path Integral Control code. Finally, we compare computational performance to other popular implementations of Model Predictive Path Integral Control over a variety of GPUs to show the real-time capabilities our library can allow for. Library code can be found at: https://acdslab.github.io/mppi-generic-website/ .