Nonlinear Robust Optimization for Planning and Control

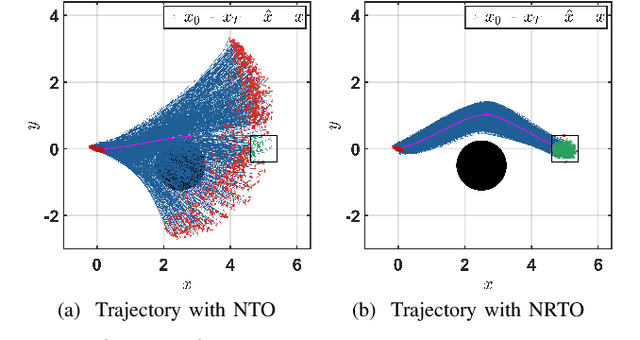
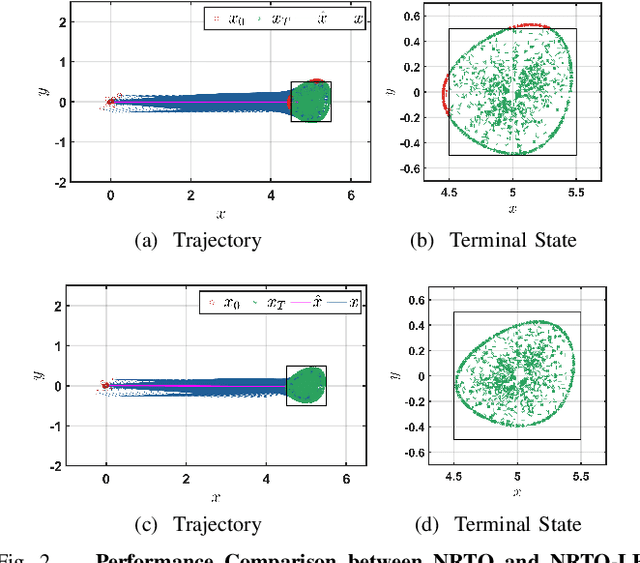
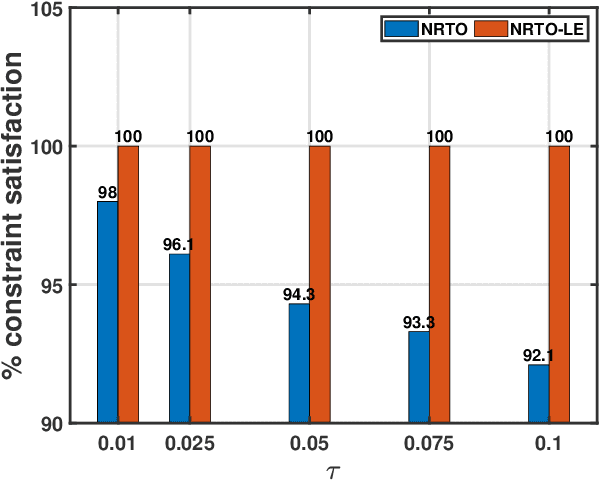
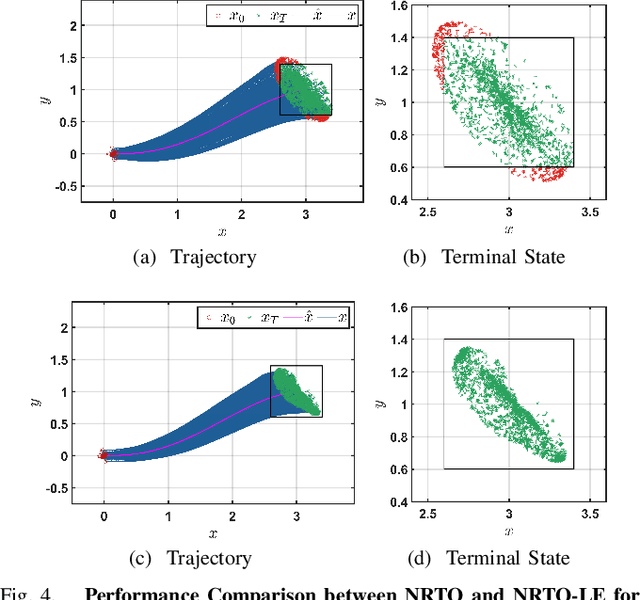
This paper presents a novel robust trajectory optimization method for constrained nonlinear dynamical systems subject to unknown bounded disturbances. In particular, we seek optimal control policies that remain robustly feasible with respect to all possible realizations of the disturbances within prescribed uncertainty sets. To address this problem, we introduce a bi-level optimization algorithm. The outer level employs a trust-region successive convexification approach which relies on linearizing the nonlinear dynamics and robust constraints. The inner level involves solving the resulting linearized robust optimization problems, for which we derive tractable convex reformulations and present an Augmented Lagrangian method for efficiently solving them. To further enhance the robustness of our methodology on nonlinear systems, we also illustrate that potential linearization errors can be effectively modeled as unknown disturbances as well. Simulation results verify the applicability of our approach in controlling nonlinear systems in a robust manner under unknown disturbances. The promise of effectively handling approximation errors in such successive linearization schemes from a robust optimization perspective is also highlighted.

Deep Distributed Optimization for Large-Scale Quadratic Programming

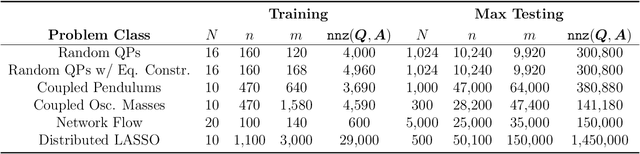
Quadratic programming (QP) forms a crucial foundation in optimization, encompassing a broad spectrum of domains and serving as the basis for more advanced algorithms. Consequently, as the scale and complexity of modern applications continue to grow, the development of efficient and reliable QP algorithms is becoming increasingly vital. In this context, this paper introduces a novel deep learning-aided distributed optimization architecture designed for tackling large-scale QP problems. First, we combine the state-of-the-art Operator Splitting QP (OSQP) method with a consensus approach to derive DistributedQP, a new method tailored for network-structured problems, with convergence guarantees to optimality. Subsequently, we unfold this optimizer into a deep learning framework, leading to DeepDistributedQP, which leverages learned policies to accelerate reaching to desired accuracy within a restricted amount of iterations. Our approach is also theoretically grounded through Probably Approximately Correct (PAC)-Bayes theory, providing generalization bounds on the expected optimality gap for unseen problems. The proposed framework, as well as its centralized version DeepQP, significantly outperform their standard optimization counterparts on a variety of tasks such as randomly generated problems, optimal control, linear regression, transportation networks and others. Notably, DeepDistributedQP demonstrates strong generalization by training on small problems and scaling to solve much larger ones (up to 50K variables and 150K constraints) using the same policy. Moreover, it achieves orders-of-magnitude improvements in wall-clock time compared to OSQP. The certifiable performance guarantees of our approach are also demonstrated, ensuring higher-quality solutions over traditional optimizers.

Scaling Robust Optimization for Multi-Agent Robotic Systems: A Distributed Perspective

This paper presents a novel distributed robust optimization scheme for steering distributions of multi-agent systems under stochastic and deterministic uncertainty. Robust optimization is a subfield of optimization which aims in discovering an optimal solution that remains robustly feasible for all possible realizations of the problem parameters within a given uncertainty set. Such approaches would naturally constitute an ideal candidate for multi-robot control, where in addition to stochastic noise, there might be exogenous deterministic disturbances. Nevertheless, as these methods are usually associated with significantly high computational demands, their application to multi-agent robotics has remained limited. The scope of this work is to propose a scalable robust optimization framework that effectively addresses both types of uncertainties, while retaining computational efficiency and scalability. In this direction, we provide tractable approximations for robust constraints that are relevant in multi-robot settings. Subsequently, we demonstrate how computations can be distributed through an Alternating Direction Method of Multipliers (ADMM) approach towards achieving scalability and communication efficiency. Simulation results highlight the performance of the proposed algorithm in effectively handling both stochastic and deterministic uncertainty in multi-robot systems. The scalability of the method is also emphasized by showcasing tasks with up to 100 agents. The results of this work indicate the promise of blending robust optimization, distribution steering and distributed optimization towards achieving scalable, safe and robust multi-robot control.