Augustinos D. Saravanos
Momentum Multi-Marginal Schrödinger Bridge Matching
Jun 11, 2025Abstract:Understanding complex systems by inferring trajectories from sparse sample snapshots is a fundamental challenge in a wide range of domains, e.g., single-cell biology, meteorology, and economics. Despite advancements in Bridge and Flow matching frameworks, current methodologies rely on pairwise interpolation between adjacent snapshots. This hinders their ability to capture long-range temporal dependencies and potentially affects the coherence of the inferred trajectories. To address these issues, we introduce \textbf{Momentum Multi-Marginal Schr\"odinger Bridge Matching (3MSBM)}, a novel matching framework that learns smooth measure-valued splines for stochastic systems that satisfy multiple positional constraints. This is achieved by lifting the dynamics to phase space and generalizing stochastic bridges to be conditioned on several points, forming a multi-marginal conditional stochastic optimal control problem. The underlying dynamics are then learned by minimizing a variational objective, having fixed the path induced by the multi-marginal conditional bridge. As a matching approach, 3MSBM learns transport maps that preserve intermediate marginals throughout training, significantly improving convergence and scalability. Extensive experimentation in a series of real-world applications validates the superior performance of 3MSBM compared to existing methods in capturing complex dynamics with temporal dependencies, opening new avenues for training matching frameworks in multi-marginal settings.
Nonlinear Robust Optimization for Planning and Control
Apr 06, 2025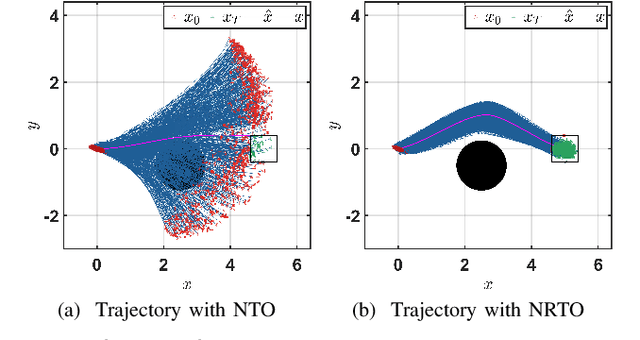
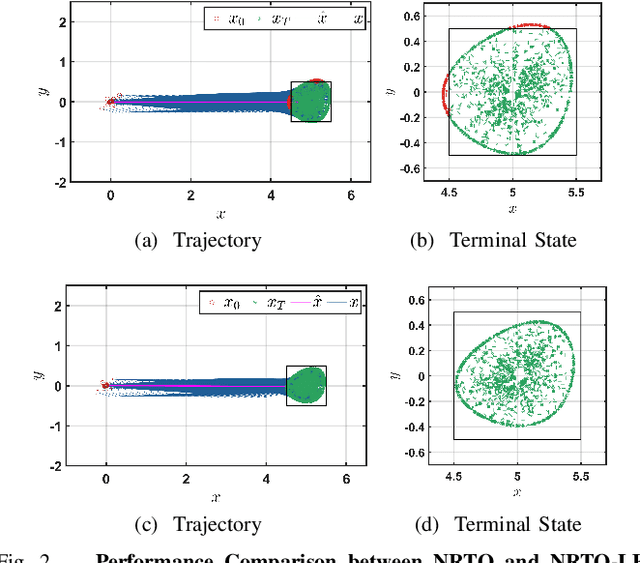
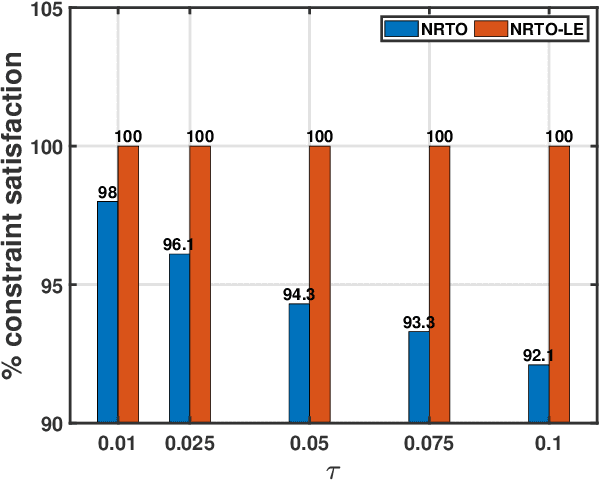
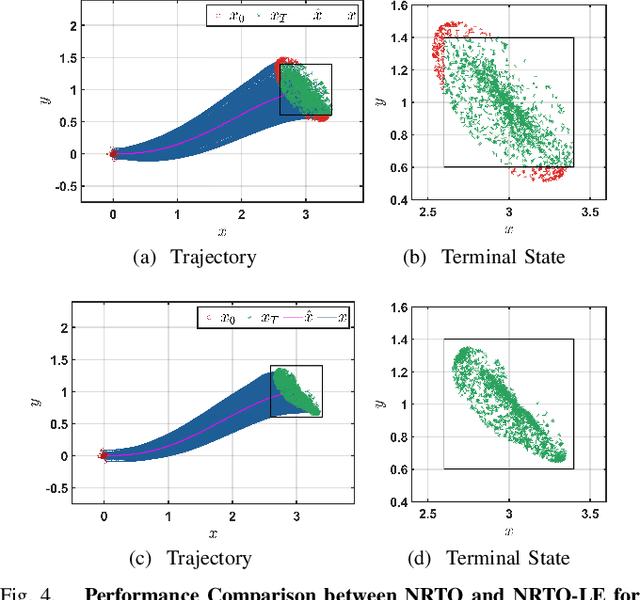
Abstract:This paper presents a novel robust trajectory optimization method for constrained nonlinear dynamical systems subject to unknown bounded disturbances. In particular, we seek optimal control policies that remain robustly feasible with respect to all possible realizations of the disturbances within prescribed uncertainty sets. To address this problem, we introduce a bi-level optimization algorithm. The outer level employs a trust-region successive convexification approach which relies on linearizing the nonlinear dynamics and robust constraints. The inner level involves solving the resulting linearized robust optimization problems, for which we derive tractable convex reformulations and present an Augmented Lagrangian method for efficiently solving them. To further enhance the robustness of our methodology on nonlinear systems, we also illustrate that potential linearization errors can be effectively modeled as unknown disturbances as well. Simulation results verify the applicability of our approach in controlling nonlinear systems in a robust manner under unknown disturbances. The promise of effectively handling approximation errors in such successive linearization schemes from a robust optimization perspective is also highlighted.
Deep Distributed Optimization for Large-Scale Quadratic Programming
Dec 11, 2024
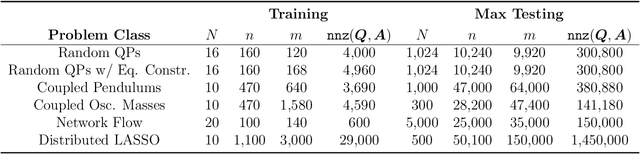


Abstract:Quadratic programming (QP) forms a crucial foundation in optimization, encompassing a broad spectrum of domains and serving as the basis for more advanced algorithms. Consequently, as the scale and complexity of modern applications continue to grow, the development of efficient and reliable QP algorithms is becoming increasingly vital. In this context, this paper introduces a novel deep learning-aided distributed optimization architecture designed for tackling large-scale QP problems. First, we combine the state-of-the-art Operator Splitting QP (OSQP) method with a consensus approach to derive DistributedQP, a new method tailored for network-structured problems, with convergence guarantees to optimality. Subsequently, we unfold this optimizer into a deep learning framework, leading to DeepDistributedQP, which leverages learned policies to accelerate reaching to desired accuracy within a restricted amount of iterations. Our approach is also theoretically grounded through Probably Approximately Correct (PAC)-Bayes theory, providing generalization bounds on the expected optimality gap for unseen problems. The proposed framework, as well as its centralized version DeepQP, significantly outperform their standard optimization counterparts on a variety of tasks such as randomly generated problems, optimal control, linear regression, transportation networks and others. Notably, DeepDistributedQP demonstrates strong generalization by training on small problems and scaling to solve much larger ones (up to 50K variables and 150K constraints) using the same policy. Moreover, it achieves orders-of-magnitude improvements in wall-clock time compared to OSQP. The certifiable performance guarantees of our approach are also demonstrated, ensuring higher-quality solutions over traditional optimizers.
Operator Splitting Covariance Steering for Safe Stochastic Nonlinear Control
Nov 18, 2024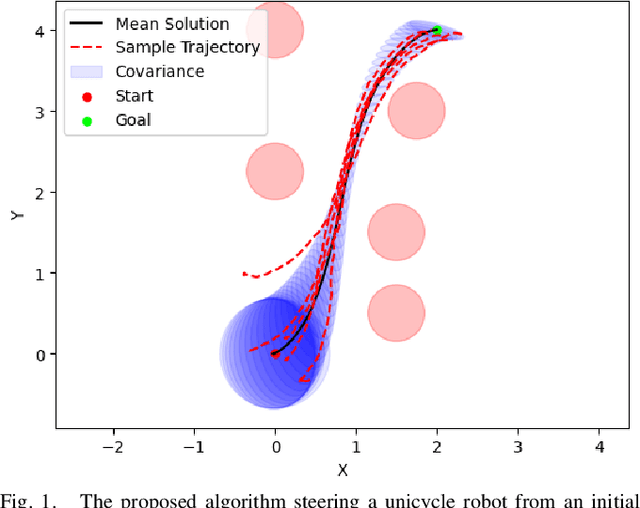
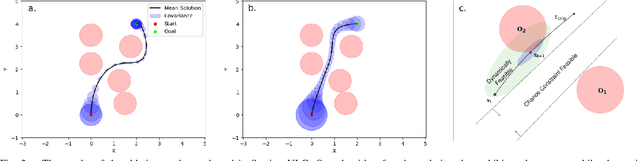

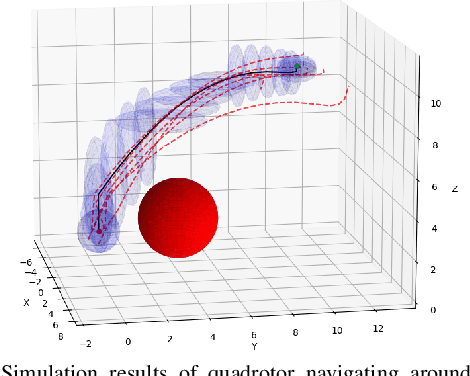
Abstract:Most robotics applications are typically accompanied with safety restrictions that need to be satisfied with a high degree of confidence even in environments under uncertainty. Controlling the state distribution of a system and enforcing such specifications as distribution constraints is a promising approach for meeting such requirements. In this direction, covariance steering (CS) is an increasingly popular stochastic optimal control (SOC) framework for designing safe controllers via explicit constraints on the system covariance. Nevertheless, a major challenge in applying CS methods to systems with the nonlinear dynamics and chance constraints common in robotics is that the approximations needed are conservative and highly sensitive to the point of approximation. This can cause sequential convex programming methods to converge to poor local minima or incorrectly report problems as infeasible due to shifting constraints. This paper presents a novel algorithm for solving chance-constrained nonlinear CS problems that directly addresses this challenge. Specifically, we propose an operator-splitting approach that temporarily separates the main problem into subproblems that can be solved in parallel. The benefit of this relaxation lies in the fact that it does not require all iterates to satisfy all constraints simultaneously prior to convergence, thus enhancing the exploration capabilities of the algorithm for finding better solutions. Simulation results verify the ability of the proposed method to find higher quality solutions under stricter safety constraints than standard methods on a variety of robotic systems. Finally, the applicability of the algorithm on real systems is confirmed through hardware demonstrations.
Scaling Robust Optimization for Multi-Agent Robotic Systems: A Distributed Perspective
Feb 26, 2024Abstract:This paper presents a novel distributed robust optimization scheme for steering distributions of multi-agent systems under stochastic and deterministic uncertainty. Robust optimization is a subfield of optimization which aims in discovering an optimal solution that remains robustly feasible for all possible realizations of the problem parameters within a given uncertainty set. Such approaches would naturally constitute an ideal candidate for multi-robot control, where in addition to stochastic noise, there might be exogenous deterministic disturbances. Nevertheless, as these methods are usually associated with significantly high computational demands, their application to multi-agent robotics has remained limited. The scope of this work is to propose a scalable robust optimization framework that effectively addresses both types of uncertainties, while retaining computational efficiency and scalability. In this direction, we provide tractable approximations for robust constraints that are relevant in multi-robot settings. Subsequently, we demonstrate how computations can be distributed through an Alternating Direction Method of Multipliers (ADMM) approach towards achieving scalability and communication efficiency. Simulation results highlight the performance of the proposed algorithm in effectively handling both stochastic and deterministic uncertainty in multi-robot systems. The scalability of the method is also emphasized by showcasing tasks with up to 100 agents. The results of this work indicate the promise of blending robust optimization, distribution steering and distributed optimization towards achieving scalable, safe and robust multi-robot control.
Distributed Hierarchical Distribution Control for Very-Large-Scale Clustered Multi-Agent Systems
May 30, 2023Abstract:As the scale and complexity of multi-agent robotic systems are subject to a continuous increase, this paper considers a class of systems labeled as Very-Large-Scale Multi-Agent Systems (VLMAS) with dimensionality that can scale up to the order of millions of agents. In particular, we consider the problem of steering the state distributions of all agents of a VLMAS to prescribed target distributions while satisfying probabilistic safety guarantees. Based on the key assumption that such systems often admit a multi-level hierarchical clustered structure - where the agents are organized into cliques of different levels - we associate the control of such cliques with the control of distributions, and introduce the Distributed Hierarchical Distribution Control (DHDC) framework. The proposed approach consists of two sub-frameworks. The first one, Distributed Hierarchical Distribution Estimation (DHDE), is a bottom-up hierarchical decentralized algorithm which links the initial and target configurations of the cliques of all levels with suitable Gaussian distributions. The second part, Distributed Hierarchical Distribution Steering (DHDS), is a top-down hierarchical distributed method that steers the distributions of all cliques and agents from the initial to the targets ones assigned by DHDE. Simulation results that scale up to two million agents demonstrate the effectiveness and scalability of the proposed framework. The increased computational efficiency and safety performance of DHDC against related methods is also illustrated. The results of this work indicate the importance of hierarchical distribution control approaches towards achieving safe and scalable solutions for the control of VLMAS. A video with all results is available in https://youtu.be/0QPyR4bD2q0 .
Improved Exploration for Safety-Embedded Differential Dynamic Programming Using Tolerant Barrier States
Mar 06, 2023Abstract:In this paper, we introduce Tolerant Discrete Barrier States (T-DBaS), a novel safety-embedding technique for trajectory optimization with enhanced exploratory capabilities. The proposed approach generalizes the standard discrete barrier state (DBaS) method by accommodating temporary constraint violation during the optimization process while still approximating its safety guarantees. Consequently, the proposed approach eliminates the DBaS's safe nominal trajectories assumption, while enhancing its exploration effectiveness for escaping local minima. Towards applying T-DBaS to safety-critical autonomous robotics, we combine it with Differential Dynamic Programming (DDP), leading to the proposed safe trajectory optimization method T-DBaS-DDP, which inherits the convergence and scalability properties of the solver. The effectiveness of the T-DBaS algorithm is verified on differential drive robot and quadrotor simulations. In addition, we compare against the classical DBaS-DDP as well as Augmented-Lagrangian DDP (AL-DDP) in extensive numerical comparisons that demonstrate the proposed method's competitive advantages. Finally, the applicability of the proposed approach is verified through hardware experiments on the Georgia Tech Robotarium platform.
Distributed Model Predictive Covariance Steering
Dec 01, 2022

Abstract:This paper proposes Distributed Model Predictive Covariance Steering (DMPCS), a novel method for safe multi-robot control under uncertainty. The scope of our approach is to blend covariance steering theory, distributed optimization and model predictive control (MPC) into a single methodology that is safe, scalable and decentralized. Initially, we pose a problem formulation that uses the Wasserstein distance to steer the state distributions of a multi-robot team to desired targets, and probabilistic constraints to ensure safety. We then transform this problem into a finite-dimensional optimization one by utilizing a disturbance feedback policy parametrization for covariance steering and a tractable approximation of the safety constraints. To solve the latter problem, we derive a decentralized consensus-based algorithm using the Alternating Direction Method of Multipliers (ADMM). This method is then extended to a receding horizon form, which yields the proposed DMPCS algorithm. Simulation experiments on large-scale problems with up to hundreds of robots successfully demonstrate the effectiveness and scalability of DMPCS. Its superior capability in achieving safety is also highlighted through a comparison against a standard stochastic MPC approach. A video with all simulation experiments is available in https://youtu.be/Hks-0BRozxA.
Decentralized Safe Multi-agent Stochastic Optimal Control using Deep FBSDEs and ADMM
Feb 22, 2022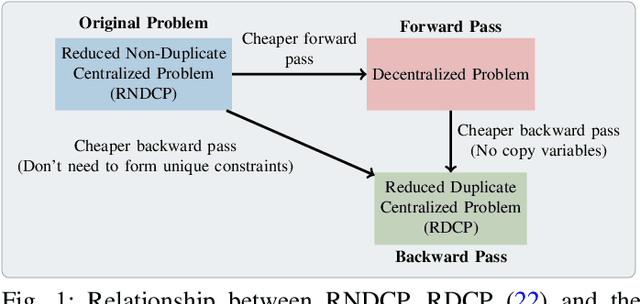
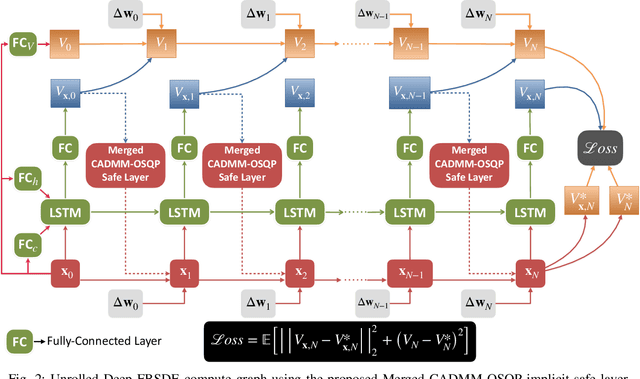
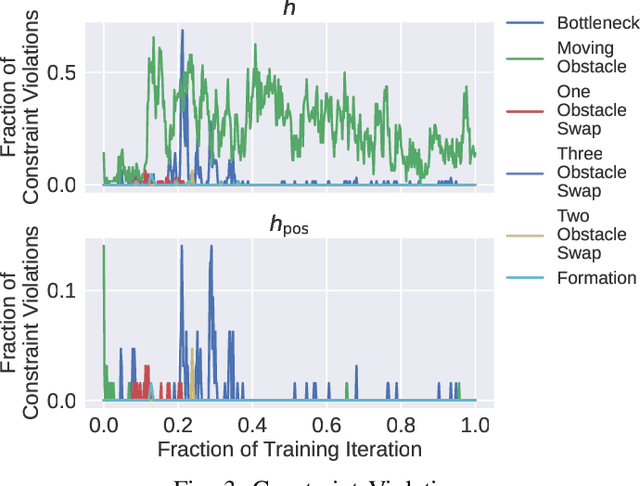

Abstract:In this work, we propose a novel safe and scalable decentralized solution for multi-agent control in the presence of stochastic disturbances. Safety is mathematically encoded using stochastic control barrier functions and safe controls are computed by solving quadratic programs. Decentralization is achieved by augmenting to each agent's optimization variables, copy variables, for its neighbors. This allows us to decouple the centralized multi-agent optimization problem. However, to ensure safety, neighboring agents must agree on "what is safe for both of us" and this creates a need for consensus. To enable safe consensus solutions, we incorporate an ADMM-based approach. Specifically, we propose a Merged CADMM-OSQP implicit neural network layer, that solves a mini-batch of both, local quadratic programs as well as the overall consensus problem, as a single optimization problem. This layer is embedded within a Deep FBSDEs network architecture at every time step, to facilitate end-to-end differentiable, safe and decentralized stochastic optimal control. The efficacy of the proposed approach is demonstrated on several challenging multi-robot tasks in simulation. By imposing requirements on safety specified by collision avoidance constraints, the safe operation of all agents is ensured during the entire training process. We also demonstrate superior scalability in terms of computational and memory savings as compared to a centralized approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge