Transformer-Based Model Predictive Path Integral Control

This paper presents a novel approach to improve the Model Predictive Path Integral (MPPI) control by using a transformer to initialize the mean control sequence. Traditional MPPI methods often struggle with sample efficiency and computational costs due to suboptimal initial rollouts. We propose TransformerMPPI, which uses a transformer trained on historical control data to generate informed initial mean control sequences. TransformerMPPI combines the strengths of the attention mechanism in transformers and sampling-based control, leading to improved computational performance and sample efficiency. The ability of the transformer to capture long-horizon patterns in optimal control sequences allows TransformerMPPI to start from a more informed control sequence, reducing the number of samples required, and accelerating convergence to optimal control sequence. We evaluate our method on various control tasks, including avoidance of collisions in a 2D environment and autonomous racing in the presence of static and dynamic obstacles. Numerical simulations demonstrate that TransformerMPPI consistently outperforms traditional MPPI algorithms in terms of overall average cost, sample efficiency, and computational speed in the presence of static and dynamic obstacles.

Decentralized Safe and Scalable Multi-Agent Control under Limited Actuation

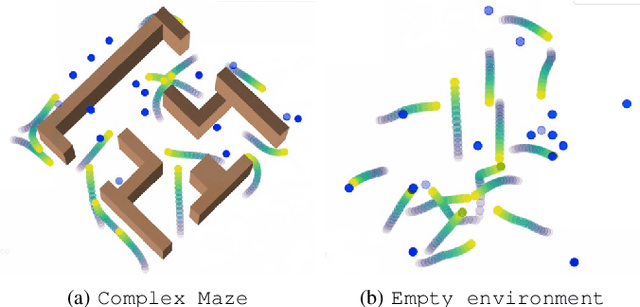
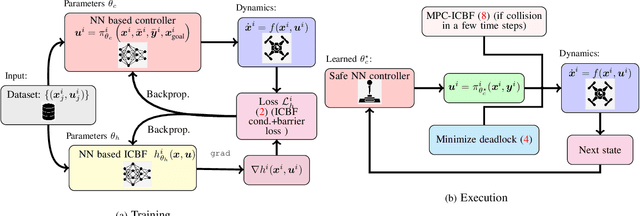
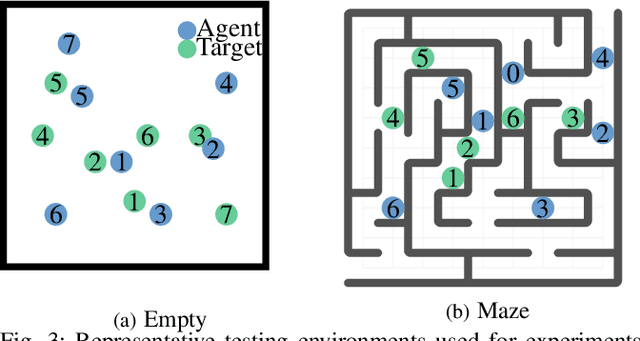
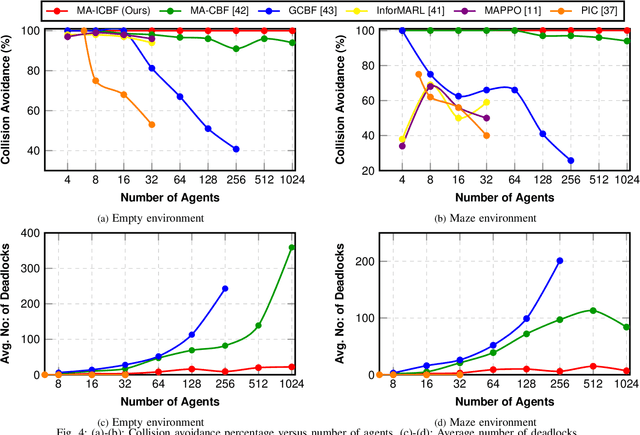
To deploy safe and agile robots in cluttered environments, there is a need to develop fully decentralized controllers that guarantee safety, respect actuation limits, prevent deadlocks, and scale to thousands of agents. Current approaches fall short of meeting all these goals: optimization-based methods ensure safety but lack scalability, while learning-based methods scale but do not guarantee safety. We propose a novel algorithm to achieve safe and scalable control for multiple agents under limited actuation. Specifically, our approach includes: $(i)$ learning a decentralized neural Integral Control Barrier function (neural ICBF) for scalable, input-constrained control, $(ii)$ embedding a lightweight decentralized Model Predictive Control-based Integral Control Barrier Function (MPC-ICBF) into the neural network policy to ensure safety while maintaining scalability, and $(iii)$ introducing a novel method to minimize deadlocks based on gradient-based optimization techniques from machine learning to address local minima in deadlocks. Our numerical simulations show that this approach outperforms state-of-the-art multi-agent control algorithms in terms of safety, input constraint satisfaction, and minimizing deadlocks. Additionally, we demonstrate strong generalization across scenarios with varying agent counts, scaling up to 1000 agents.

TransformerMPC: Accelerating Model Predictive Control via Transformers

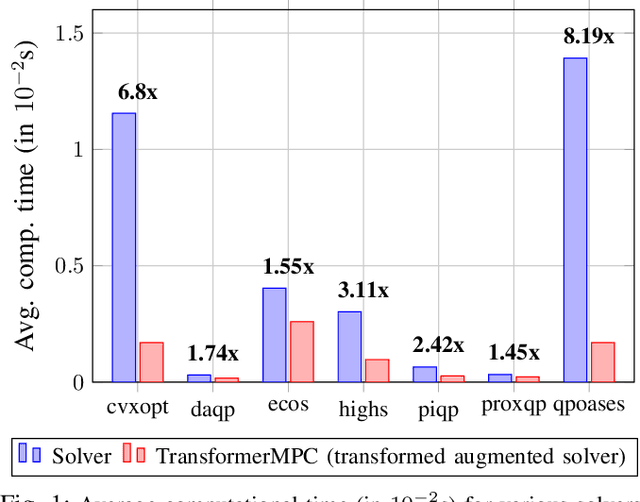
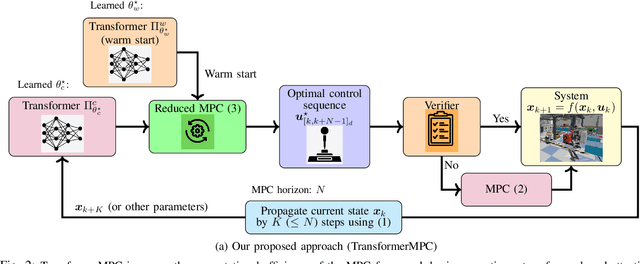
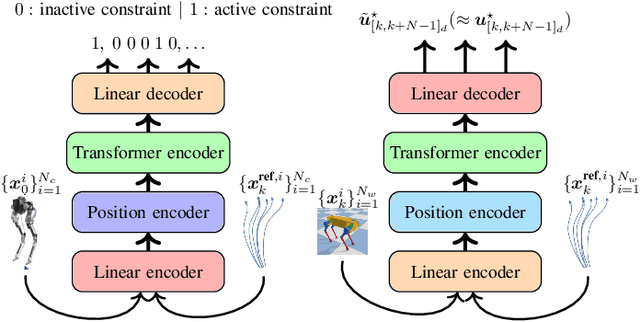
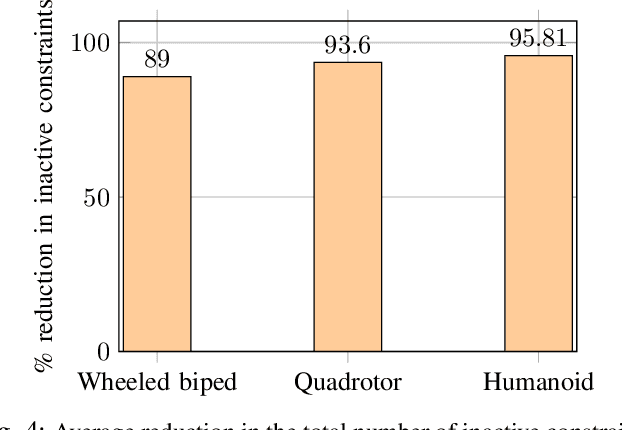
In this paper, we address the problem of reducing the computational burden of Model Predictive Control (MPC) for real-time robotic applications. We propose TransformerMPC, a method that enhances the computational efficiency of MPC algorithms by leveraging the attention mechanism in transformers for both online constraint removal and better warm start initialization. Specifically, TransformerMPC accelerates the computation of optimal control inputs by selecting only the active constraints to be included in the MPC problem, while simultaneously providing a warm start to the optimization process. This approach ensures that the original constraints are satisfied at optimality. TransformerMPC is designed to be seamlessly integrated with any MPC solver, irrespective of its implementation. To guarantee constraint satisfaction after removing inactive constraints, we perform an offline verification to ensure that the optimal control inputs generated by the MPC solver meet all constraints. The effectiveness of TransformerMPC is demonstrated through extensive numerical simulations on complex robotic systems, achieving up to 35x improvement in runtime without any loss in performance.

Path Integral Control with Rollout Clustering and Dynamic Obstacles

Model Predictive Path Integral (MPPI) control has proven to be a powerful tool for the control of uncertain systems (such as systems subject to disturbances and systems with unmodeled dynamics). One important limitation of the baseline MPPI algorithm is that it does not utilize simulated trajectories to their fullest extent. For one, it assumes that the average of all trajectories weighted by their performance index will be a safe trajectory. In this paper, multiple examples are shown where the previous assumption does not hold, and a trajectory clustering technique is presented that reduces the chances of the weighted average crossing in an unsafe region. Secondly, MPPI does not account for dynamic obstacles, so the authors put forward a novel cost function that accounts for dynamic obstacles without adding significant computation time to the overall algorithm. The novel contributions proposed in this paper were evaluated with extensive simulations to demonstrate improvements upon the state-of-the-art MPPI techniques.

Decentralized Multi-Robot Social Navigation in Constrained Environments via Game-Theoretic Control Barrier Functions

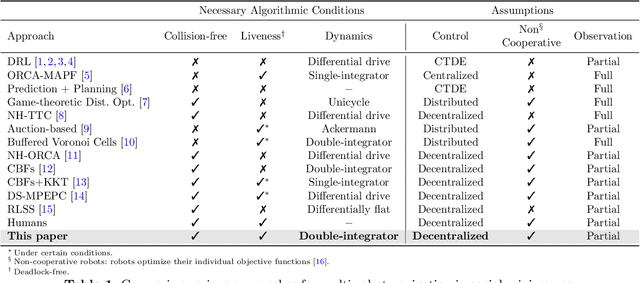
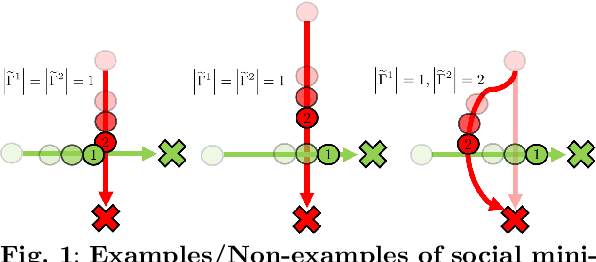
We present an approach to ensure safe and deadlock-free navigation for decentralized multi-robot systems operating in constrained environments, including doorways and intersections. Although many solutions have been proposed to ensure safety, preventing deadlocks in a decentralized fashion with global consensus remains an open problem. We first formalize the objective as a non-cooperative, non-communicative, partially observable multi-robot navigation problem in constrained spaces with multiple conflicting agents, which we term as \emph{social mini-games}. Our approach to ensuring liveness rests on two novel insights: $(i)$ there exists a mixed-strategy Nash equilibrium that allows decentralized robots to perturb their state onto \textit{liveness sets} i.e. states where robots are deadlock-free and $(ii)$ forward invariance of liveness sets can be achieved identical to how control barrier functions (CBFs) guarantee forward invariance of safety sets. We evaluate our approach in simulation as well on physical robots using F$1/10$ robots, a Clearpath Jackal, as well as a Boston Dynamics Spot in a doorway and corridor intersection scenario. Compared to both fully decentralized and centralized approaches with and without deadlock resolution capabilities, we demonstrate that our approach results in safer, more efficient, and smoother navigation, based on a comprehensive set of metrics including success rate, collision rate, stop time, change in velocity, path deviation, time-to-goal, and flow rate.

Distributed Model Predictive Covariance Steering

This paper proposes Distributed Model Predictive Covariance Steering (DMPCS), a novel method for safe multi-robot control under uncertainty. The scope of our approach is to blend covariance steering theory, distributed optimization and model predictive control (MPC) into a single methodology that is safe, scalable and decentralized. Initially, we pose a problem formulation that uses the Wasserstein distance to steer the state distributions of a multi-robot team to desired targets, and probabilistic constraints to ensure safety. We then transform this problem into a finite-dimensional optimization one by utilizing a disturbance feedback policy parametrization for covariance steering and a tractable approximation of the safety constraints. To solve the latter problem, we derive a decentralized consensus-based algorithm using the Alternating Direction Method of Multipliers (ADMM). This method is then extended to a receding horizon form, which yields the proposed DMPCS algorithm. Simulation experiments on large-scale problems with up to hundreds of robots successfully demonstrate the effectiveness and scalability of DMPCS. Its superior capability in achieving safety is also highlighted through a comparison against a standard stochastic MPC approach. A video with all simulation experiments is available in https://youtu.be/Hks-0BRozxA.

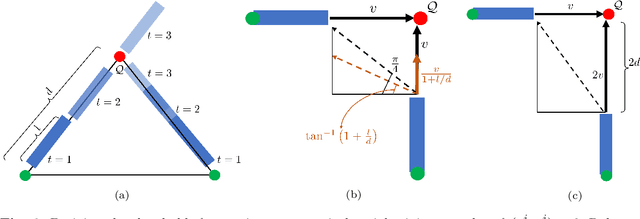
Smooth time optimal trajectory generation for drones

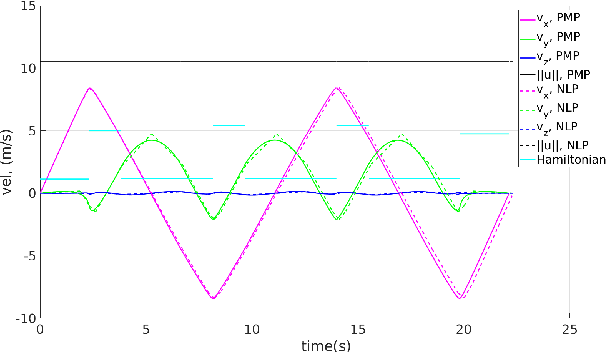
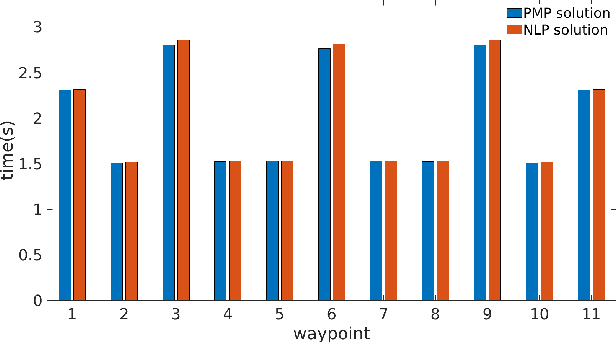
In this paper, we address a minimum-time steering problem for a drone modeled as point mass with bounded acceleration, across a set of desired waypoints in the presence of gravity. We first provide a method to solve for the minimum-time control input that will steer the point mass between two waypoints based on a continuous-time problem formulation which we address by using Pontryagin's Minimum Principle. Subsequently, we solve for the time-optimal trajectory across the given set of waypoints by discretizing in the time domain and formulating the minimum-time problem as a nonlinear program (NLP). The velocities at each waypoint obtained from solving the NLP in the discretized domain are then used as boundary conditions to extend our two-point solution across those multiple waypoints. We apply this planning methodology to execute a surveying task that minimizes the time taken to completely explore a target area or volume. Numerical simulations and theoretical analyses of this new planning methodology are presented. The results from our approach are also compared to traditional polynomial trajectories like minimum snap planning.

Neural Koopman Lyapunov Control

Learning and synthesizing stabilizing controllers for unknown nonlinear systems is a challenging problem for real-world and industrial applications. Koopman operator theory allow one to analyze nonlinear systems through the lens of linear systems and nonlinear control systems through the lens of bilinear control systems. The key idea of these methods, lies in the transformation of the coordinates of the nonlinear system into the Koopman observables, which are coordinates that allow the representation of the original system (control system) as a higher dimensional linear (bilinear control) system. However, for nonlinear control systems, the bilinear control model obtained by applying Koopman operator based learning methods is not necessarily stabilizable and therefore, the existence of a stabilizing feedback control is not guaranteed which is crucial for many real world applications. Simultaneous identification of these stabilizable Koopman based bilinear control systems as well as the associated Koopman observables is still an open problem. In this paper, we propose a framework to identify and construct these stabilizable bilinear models and its associated observables from data by simultaneously learning a bilinear Koopman embedding for the underlying unknown nonlinear control system as well as a Control Lyapunov Function (CLF) for the Koopman based bilinear model using a learner and falsifier. Our proposed approach thereby provides provable guarantees of global asymptotic stability for the nonlinear control systems with unknown dynamics. Numerical simulations are provided to validate the efficacy of our proposed class of stabilizing feedback controllers for unknown nonlinear systems.

Collision Avoidance Using Spherical Harmonics

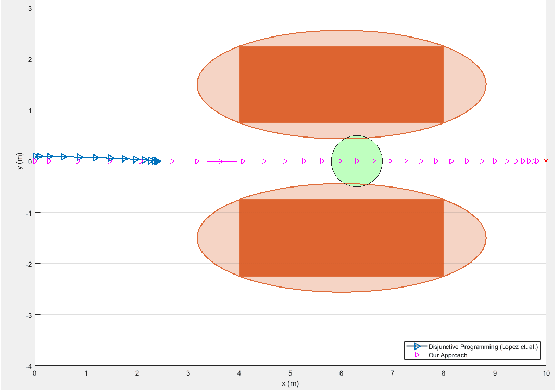
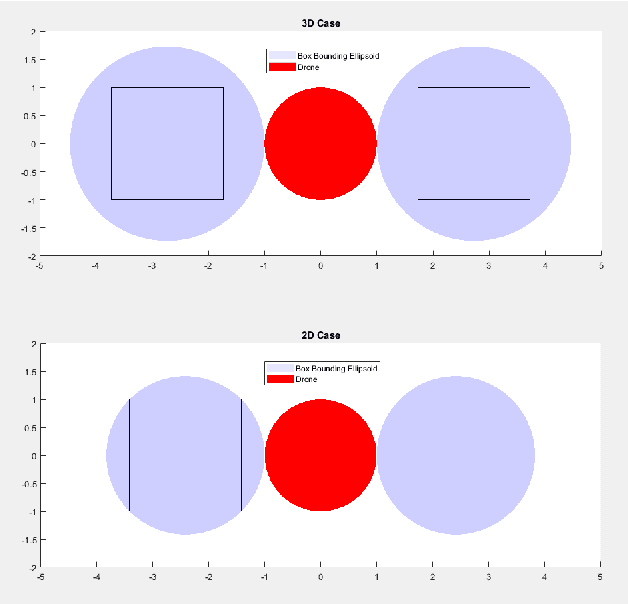
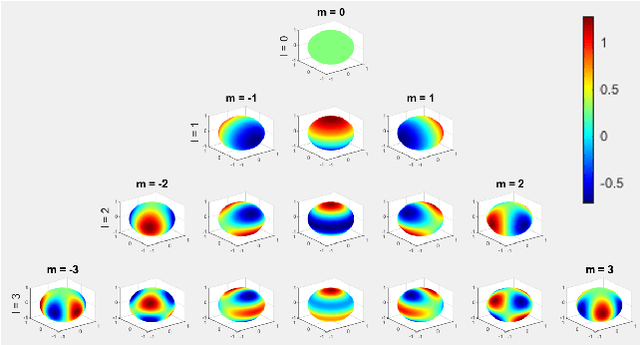
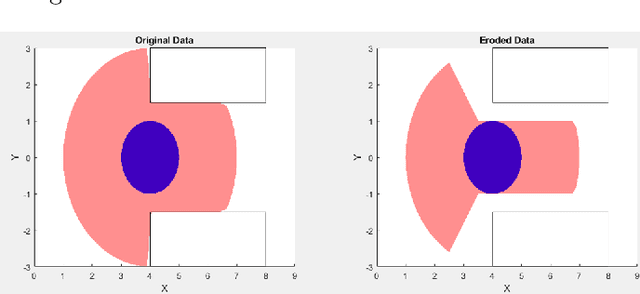
In this paper, we propose a novel optimization-based trajectory planner that utilizes spherical harmonics to estimate the collision-free solution space around an agent. The space is estimated using a constrained over-determined least-squares estimator to determine the parameters that define a spherical harmonic approximation at a given time step. Since spherical harmonics produce star-convex shapes, the planner can consider all paths that are in line-of-sight for the agent within a given radius. This contrasts with other state-of-the-art planners that generate trajectories by estimating obstacle boundaries with rough approximations and using heuristic rules to prune a solution space into one that can be easily explored. Those methods cause the trajectory planner to be overly conservative in environments where an agent must get close to obstacles to accomplish a goal. Our method is shown to perform on-par with other path planners and surpass these planners in certain environments. It generates feasible trajectories while still running in real-time and guaranteeing safety when a valid solution exists.

Collision Avoidance for Unmanned Aerial Vehicles in the Presence of Static and Moving Obstacles

This paper presents a new collision avoidance procedure for unmanned aerial vehicles in the presence of static and moving obstacles. The proposed procedure is based on a new form of local parametrized guidance vector fields, called collision avoidance vector fields, that produce smooth and intuitive maneuvers around obstacles. The maneuvers follow nominal collision-free paths which we refer to as streamlines of the collision avoidance vector fields. In the case of multiple obstacles, the proposed procedure determines a mixed vector field that blends the collision avoidance vector field of each obstacle and assumes its form whenever a pre-defined distance threshold is reached. Then, in accordance to the computed guidance vector fields, different collision avoidance controllers that generate collision-free maneuvers are developed. Furthermore, it is shown that any tracking controller with convergence guarantees can be used with the avoidance controllers to track the streamlines of the collision avoidance vector fields. Finally, numerical simulations demonstrate the efficacy of the proposed approach and its ability to avoid collisions with static and moving pop-up threats in three different practical scenarios.