Decentralized Safe and Scalable Multi-Agent Control under Limited Actuation

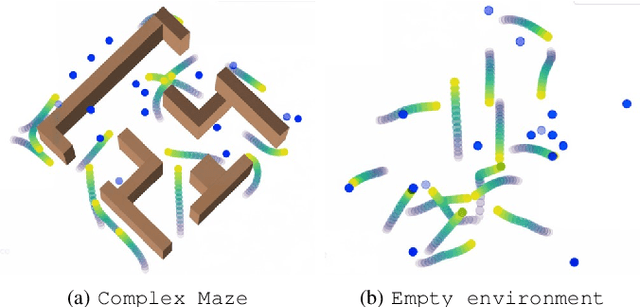
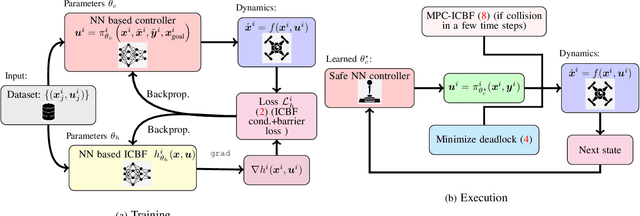
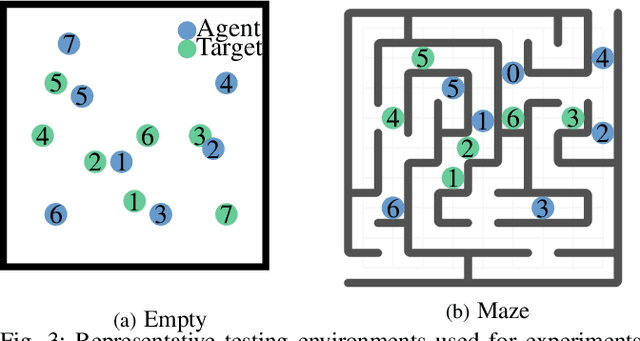
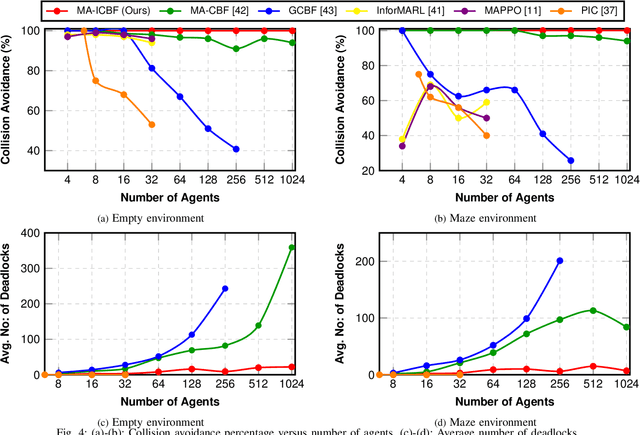
To deploy safe and agile robots in cluttered environments, there is a need to develop fully decentralized controllers that guarantee safety, respect actuation limits, prevent deadlocks, and scale to thousands of agents. Current approaches fall short of meeting all these goals: optimization-based methods ensure safety but lack scalability, while learning-based methods scale but do not guarantee safety. We propose a novel algorithm to achieve safe and scalable control for multiple agents under limited actuation. Specifically, our approach includes: $(i)$ learning a decentralized neural Integral Control Barrier function (neural ICBF) for scalable, input-constrained control, $(ii)$ embedding a lightweight decentralized Model Predictive Control-based Integral Control Barrier Function (MPC-ICBF) into the neural network policy to ensure safety while maintaining scalability, and $(iii)$ introducing a novel method to minimize deadlocks based on gradient-based optimization techniques from machine learning to address local minima in deadlocks. Our numerical simulations show that this approach outperforms state-of-the-art multi-agent control algorithms in terms of safety, input constraint satisfaction, and minimizing deadlocks. Additionally, we demonstrate strong generalization across scenarios with varying agent counts, scaling up to 1000 agents.

TransformerMPC: Accelerating Model Predictive Control via Transformers

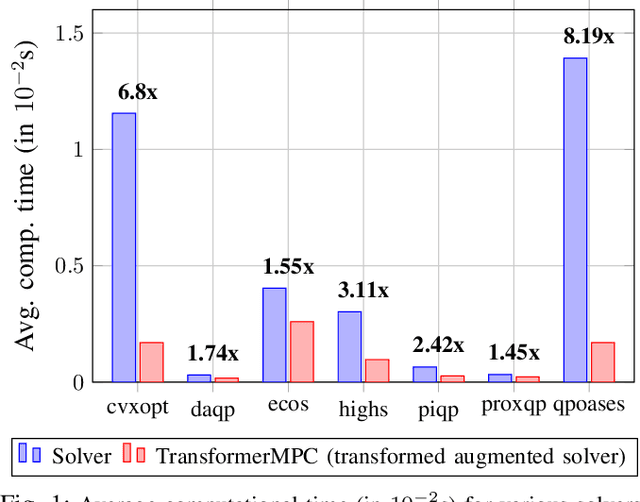
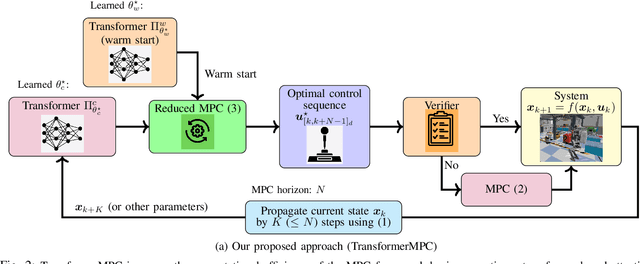
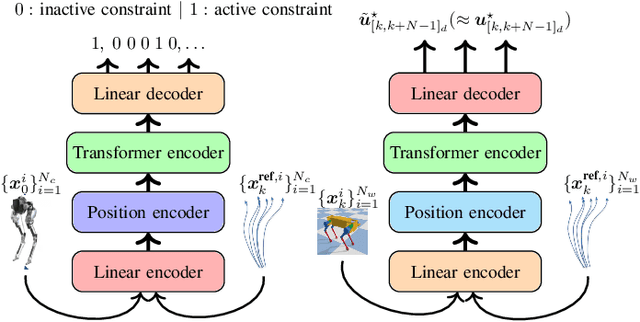
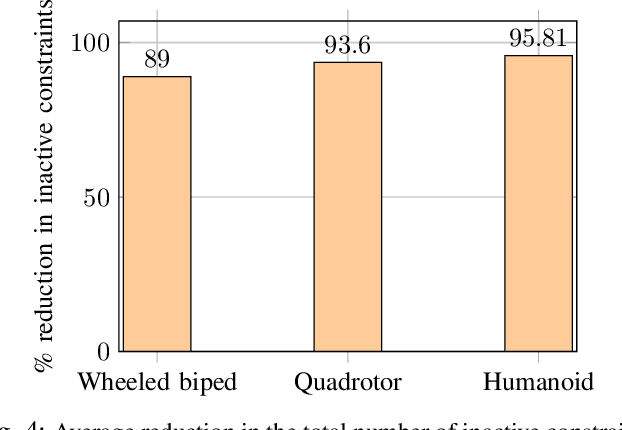
In this paper, we address the problem of reducing the computational burden of Model Predictive Control (MPC) for real-time robotic applications. We propose TransformerMPC, a method that enhances the computational efficiency of MPC algorithms by leveraging the attention mechanism in transformers for both online constraint removal and better warm start initialization. Specifically, TransformerMPC accelerates the computation of optimal control inputs by selecting only the active constraints to be included in the MPC problem, while simultaneously providing a warm start to the optimization process. This approach ensures that the original constraints are satisfied at optimality. TransformerMPC is designed to be seamlessly integrated with any MPC solver, irrespective of its implementation. To guarantee constraint satisfaction after removing inactive constraints, we perform an offline verification to ensure that the optimal control inputs generated by the MPC solver meet all constraints. The effectiveness of TransformerMPC is demonstrated through extensive numerical simulations on complex robotic systems, achieving up to 35x improvement in runtime without any loss in performance.

Decentralized Multi-Robot Social Navigation in Constrained Environments via Game-Theoretic Control Barrier Functions

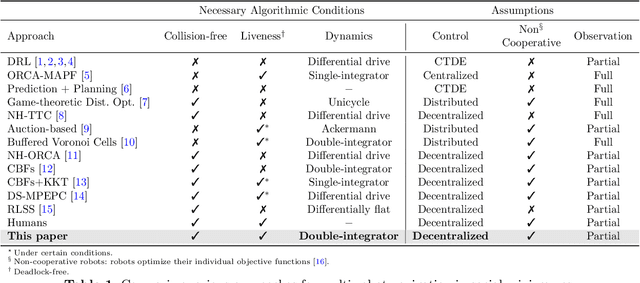
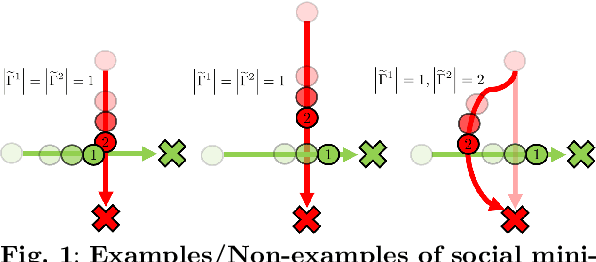
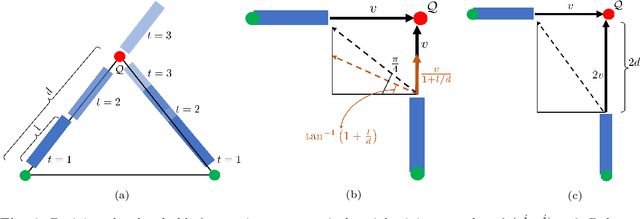
We present an approach to ensure safe and deadlock-free navigation for decentralized multi-robot systems operating in constrained environments, including doorways and intersections. Although many solutions have been proposed to ensure safety, preventing deadlocks in a decentralized fashion with global consensus remains an open problem. We first formalize the objective as a non-cooperative, non-communicative, partially observable multi-robot navigation problem in constrained spaces with multiple conflicting agents, which we term as \emph{social mini-games}. Our approach to ensuring liveness rests on two novel insights: $(i)$ there exists a mixed-strategy Nash equilibrium that allows decentralized robots to perturb their state onto \textit{liveness sets} i.e. states where robots are deadlock-free and $(ii)$ forward invariance of liveness sets can be achieved identical to how control barrier functions (CBFs) guarantee forward invariance of safety sets. We evaluate our approach in simulation as well on physical robots using F$1/10$ robots, a Clearpath Jackal, as well as a Boston Dynamics Spot in a doorway and corridor intersection scenario. Compared to both fully decentralized and centralized approaches with and without deadlock resolution capabilities, we demonstrate that our approach results in safer, more efficient, and smoother navigation, based on a comprehensive set of metrics including success rate, collision rate, stop time, change in velocity, path deviation, time-to-goal, and flow rate.

Optimal Sampling-based Motion Planning in Gaussian Belief Space for Minimum Sensing Navigation

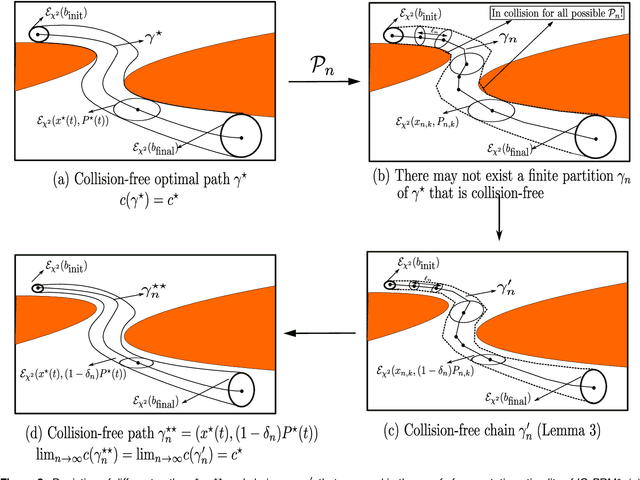
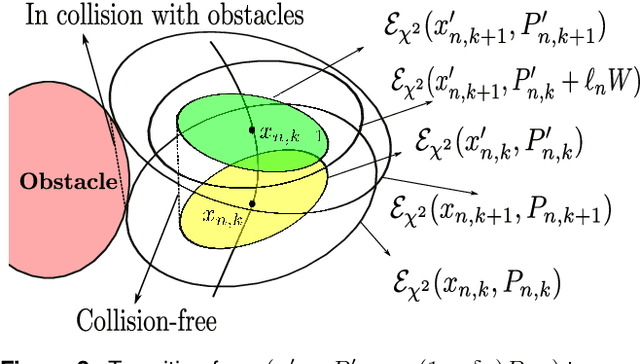
In this paper, we consider the motion planning problem in Gaussian belief space for minimum sensing navigation. Despite the extensive use of sampling-based algorithms and their rigorous analysis in the deterministic setting, there has been little formal analysis of the quality of their solutions returned by sampling algorithms in Gaussian belief space. This paper aims to address this lack of research by examining the asymptotic behavior of the cost of solutions obtained from Gaussian belief space based sampling algorithms as the number of samples increases. To that end, we propose a sampling based motion planning algorithm termed Information Geometric PRM* (IG-PRM*) for generating feasible paths that minimize a weighted sum of the Euclidean and an information-theoretic cost and show that the cost of the solution that is returned is guaranteed to approach the global optimum in the limit of large number of samples. Finally, we consider an obstacle-free scenario and compute the optimal solution using the "move and sense" strategy in literature. We then verify that the cost returned by our proposed algorithm converges to this optimal solution as the number of samples increases.

Neural Koopman Lyapunov Control

Learning and synthesizing stabilizing controllers for unknown nonlinear systems is a challenging problem for real-world and industrial applications. Koopman operator theory allow one to analyze nonlinear systems through the lens of linear systems and nonlinear control systems through the lens of bilinear control systems. The key idea of these methods, lies in the transformation of the coordinates of the nonlinear system into the Koopman observables, which are coordinates that allow the representation of the original system (control system) as a higher dimensional linear (bilinear control) system. However, for nonlinear control systems, the bilinear control model obtained by applying Koopman operator based learning methods is not necessarily stabilizable and therefore, the existence of a stabilizing feedback control is not guaranteed which is crucial for many real world applications. Simultaneous identification of these stabilizable Koopman based bilinear control systems as well as the associated Koopman observables is still an open problem. In this paper, we propose a framework to identify and construct these stabilizable bilinear models and its associated observables from data by simultaneously learning a bilinear Koopman embedding for the underlying unknown nonlinear control system as well as a Control Lyapunov Function (CLF) for the Koopman based bilinear model using a learner and falsifier. Our proposed approach thereby provides provable guarantees of global asymptotic stability for the nonlinear control systems with unknown dynamics. Numerical simulations are provided to validate the efficacy of our proposed class of stabilizing feedback controllers for unknown nonlinear systems.

Mathematical Properties of Generalized Shape Expansion-Based Motion Planning Algorithms

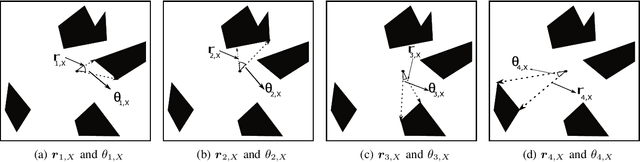
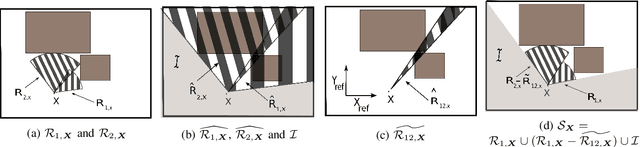
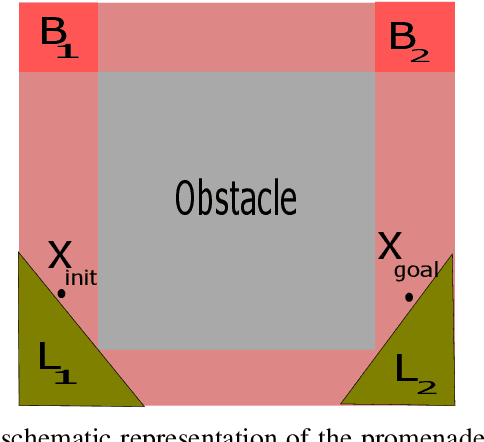
Motion planning is an essential aspect of autonomous systems and robotics and is an active area of research. A recently-proposed sampling-based motion planning algorithm, termed 'Generalized Shape Expansion' (GSE), has been shown to possess significant improvement in computational time over several existing well-established algorithms. The GSE has also been shown to be probabilistically complete. However, asymptotic optimality of the GSE is yet to be studied. To this end, in this paper we show that the GSE algorithm is not asymptotically optimal by studying its behaviour for the promenade problem. In order to obtain a probabilistically complete and asymptotically optimal generalized shape-based algorithm, a modified version of the GSE, namely 'GSE*' algorithm, is subsequently presented. The forementioned desired mathematical properties of the GSE* algorithm are justified by its detailed analysis. Numerical simulations are found to be in line with the theoretical results on the GSE* algorithm.

3D-OGSE: Online Smooth Trajectory Generation for Quadrotors using Generalized Shape Expansion in Unknown 3D Environments

In this letter, we present an online motion planning algorithm for generating smooth, collision-free trajectories for quadrotors operating in an unknown, cluttered 3D environment. Our approach constructs a non-convex safe-region termed generalized shape at each timestep, which represents the obstacle-free region in the environment. A collision-free path is computed by sampling points in the generalized shape and is used to generate a smooth, time-parameterized trajectory by minimizing snap. The generated trajectories are constrained to lie within a convex subset of the generalized shape, which ensures the quadrotor maneuvers in the local obstacle-free space. This process is repeated at each timestep to re-plan trajectories until the quadrotor reaches its goal position. We evaluate the proposed method in simulation on complex 3D environments with high obstacle densities. We observe that each re-planing computation takes $\sim1.6$ milliseconds on a single thread of an Intel Core i5-8500 3.0 GHz CPU. In addition, our method is 6-10x faster than prior online motion planning methods, and we observe less conservative behavior in complex scenarios such as narrow passages.