Steering Large Agent Populations using Mean-Field Schrodinger Bridges with Gaussian Mixture Models

The Mean-Field Schrodinger Bridge (MFSB) problem is an optimization problem aiming to find the minimum effort control policy to drive a McKean-Vlassov stochastic differential equation from one probability measure to another. In the context of multiagent control, the objective is to control the configuration of a swarm of identical, interacting cooperative agents, as captured by the time-varying probability measure of their state. Available methods for solving this problem for distributions with continuous support rely either on spatial discretizations of the problem's domain or on approximating optimal solutions using neural networks trained through stochastic optimization schemes. For agents following Linear Time-Varying dynamics, and for Gaussian Mixture Model boundary distributions, we propose a highly efficient parameterization to approximate the solutions of the corresponding MFSB in closed form, without any learning steps. Our proposed approach consists of a mixture of elementary policies, each solving a Gaussian-to-Gaussian Covariance Steering problem from the components of the initial to the components of the terminal mixture. Leveraging the semidefinite formulation of the Covariance Steering problem, our proposed solver can handle probabilistic hard constraints on the system's state, while maintaining numerical tractability. We illustrate our approach on a variety of numerical examples.

Communication-Aware Iterative Map Compression for Online Path-Planning

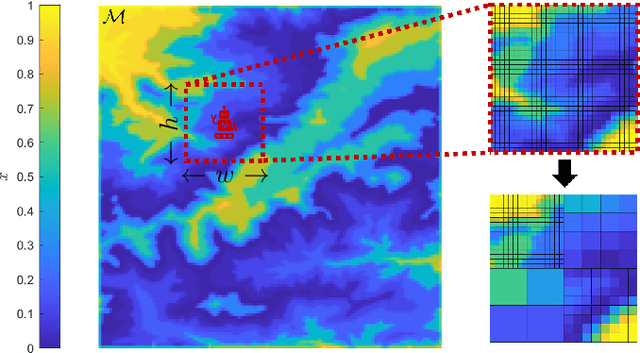
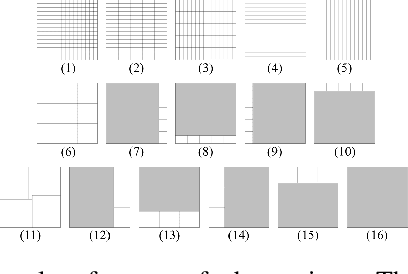
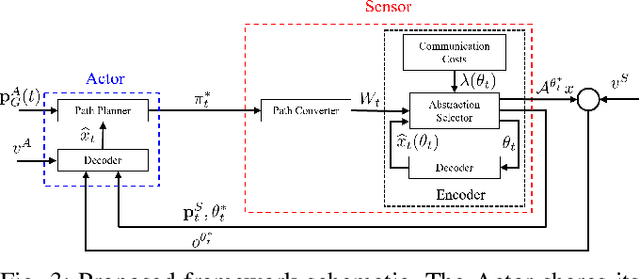
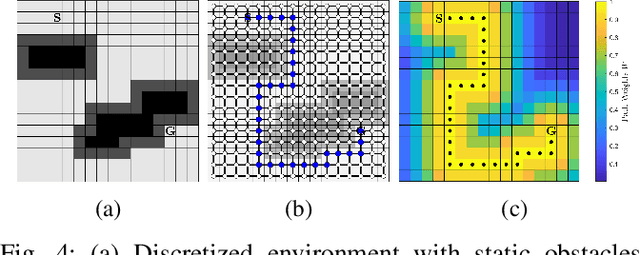
This paper addresses the problem of optimizing communicated information among heterogeneous, resource-aware robot teams to facilitate their navigation. In such operations, a mobile robot compresses its local map to assist another robot in reaching a target within an uncharted environment. The primary challenge lies in ensuring that the map compression step balances network load while transmitting only the most essential information for effective navigation. We propose a communication framework that sequentially selects the optimal map compression in a task-driven, communication-aware manner. It introduces a decoder capable of iterative map estimation, handling noise through Kalman filter techniques. The computational speed of our decoder allows for a larger compression template set compared to previous methods, and enables applications in more challenging environments. Specifically, our simulations demonstrate a remarkable 98% reduction in communicated information, compared to a framework that transmits the raw data, on a large Mars inclination map and an Earth map, all while maintaining similar planning costs. Furthermore, our method significantly reduces computational time compared to the state-of-the-art approach.

Go With the Flow: Fast Diffusion for Gaussian Mixture Models

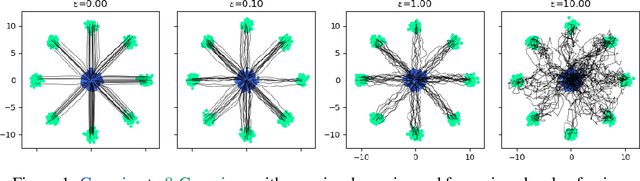
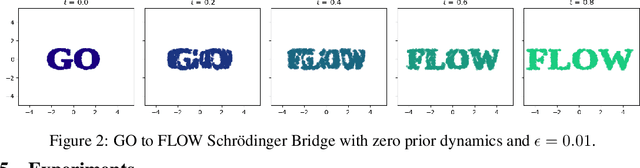
Schr\"{o}dinger Bridges (SB) are diffusion processes that steer, in finite time, a given initial distribution to another final one while minimizing a suitable cost functional. Although various methods for computing SBs have recently been proposed in the literature, most of these approaches require computationally expensive training schemes, even for solving low-dimensional problems. In this work, we propose an analytic parametrization of a set of feasible policies for steering the distribution of a dynamical system from one Gaussian Mixture Model (GMM) to another. Instead of relying on standard non-convex optimization techniques, the optimal policy within the set can be approximated as the solution of a low-dimensional linear program whose dimension scales linearly with the number of components in each mixture. Furthermore, our method generalizes naturally to more general classes of dynamical systems such as controllable Linear Time-Varying systems that cannot currently be solved using traditional neural SB approaches. We showcase the potential of this approach in low-to-moderate dimensional problems such as image-to-image translation in the latent space of an autoencoder, and various other examples. We also benchmark our approach on an Entropic Optimal Transport (EOT) problem and show that it outperforms state-of-the-art methods in cases where the boundary distributions are mixture models while requiring virtually no training.

Optimal Sampling-based Motion Planning in Gaussian Belief Space for Minimum Sensing Navigation

In this paper, we consider the motion planning problem in Gaussian belief space for minimum sensing navigation. Despite the extensive use of sampling-based algorithms and their rigorous analysis in the deterministic setting, there has been little formal analysis of the quality of their solutions returned by sampling algorithms in Gaussian belief space. This paper aims to address this lack of research by examining the asymptotic behavior of the cost of solutions obtained from Gaussian belief space based sampling algorithms as the number of samples increases. To that end, we propose a sampling based motion planning algorithm termed Information Geometric PRM* (IG-PRM*) for generating feasible paths that minimize a weighted sum of the Euclidean and an information-theoretic cost and show that the cost of the solution that is returned is guaranteed to approach the global optimum in the limit of large number of samples. Finally, we consider an obstacle-free scenario and compute the optimal solution using the "move and sense" strategy in literature. We then verify that the cost returned by our proposed algorithm converges to this optimal solution as the number of samples increases.

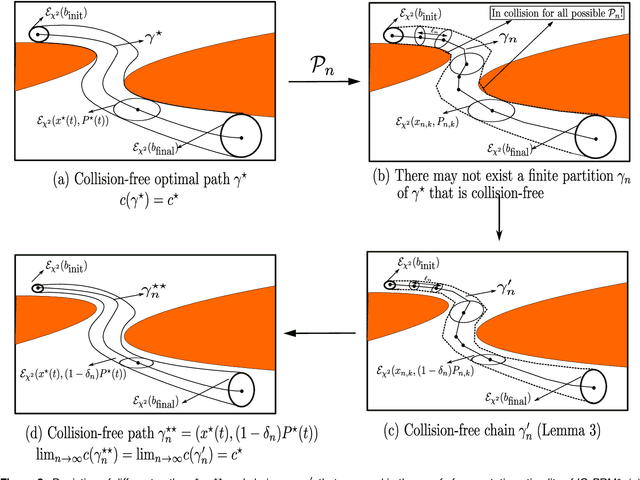
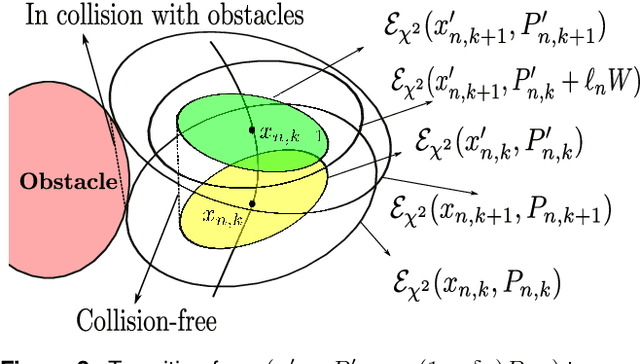
A Smoothing Algorithm for Minimum Sensing Path Plans in Gaussian Belief Space

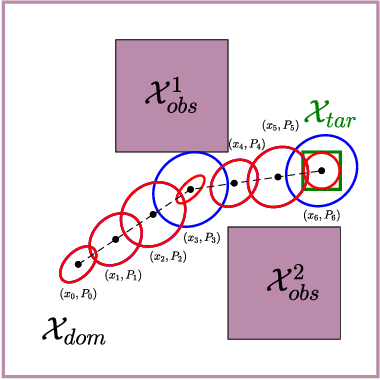
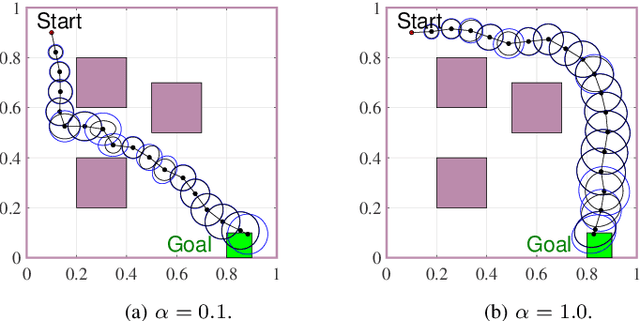
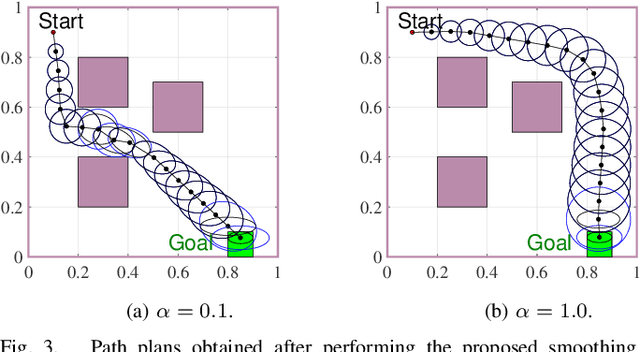
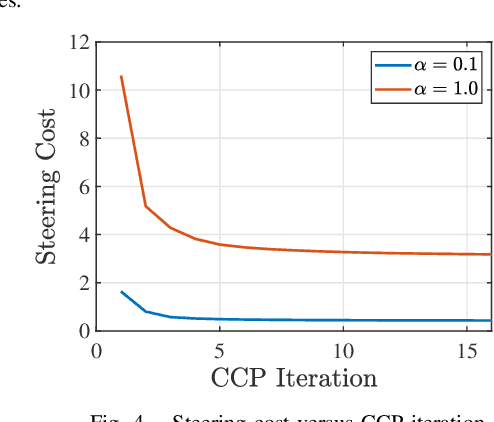
This paper explores minimum sensing navigation of robots in environments cluttered with obstacles. The general objective is to find a path plan to a goal region that requires minimal sensing effort. In [1], the information-geometric RRT* (IG-RRT*) algorithm was proposed to efficiently find such a path. However, like any stochastic sampling-based planner, the computational complexity of IG-RRT* grows quickly, impeding its use with a large number of nodes. To remedy this limitation, we suggest running IG-RRT* with a moderate number of nodes, and then using a smoothing algorithm to adjust the path obtained. To develop a smoothing algorithm, we explicitly formulate the minimum sensing path planning problem as an optimization problem. For this formulation, we introduce a new safety constraint to impose a bound on the probability of collision with obstacles in continuous-time, in contrast to the common discrete-time approach. The problem is amenable to solution via the convex-concave procedure (CCP). We develop a CCP algorithm for the formulated optimization and use this algorithm for path smoothing. We demonstrate the efficacy of the proposed approach through numerical simulations.

Gaussian Belief Space Path Planning for Minimum Sensing Navigation

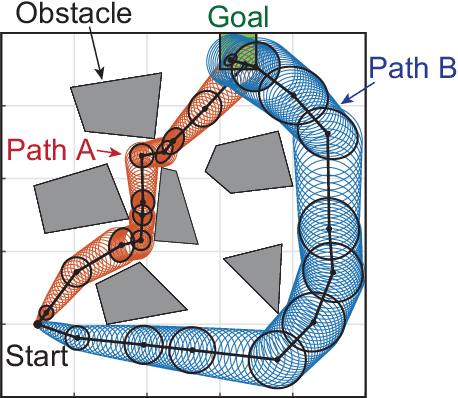
We propose a path planning methodology for a mobile robot navigating through an obstacle-filled environment to generate a reference path that is traceable with moderate sensing efforts. The desired reference path is characterized as the shortest path in an obstacle-filled Gaussian belief manifold equipped with a novel information-geometric distance function. The distance function we introduce is shown to be an asymmetric quasi-pseudometric and can be interpreted as the minimum information gain required to steer the Gaussian belief. An RRT*-based numerical solution algorithm is presented to solve the formulated shortest-path problem. To gain insight into the asymptotic optimality of the proposed algorithm, we show that the considered path length function is continuous with respect to the topology of total variation. Simulation results demonstrate that the proposed method is effective in various robot navigation scenarios to reduce sensing costs, such as the required frequency of sensor measurements and the number of sensors that must be operated simultaneously.

Dynamic Allocation of Visual Attention for Vision-based Autonomous Navigation under Data Rate Constraints

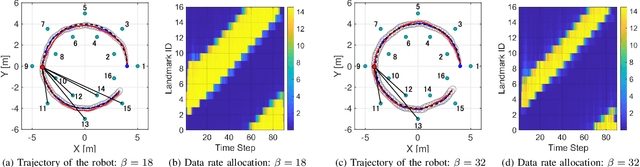
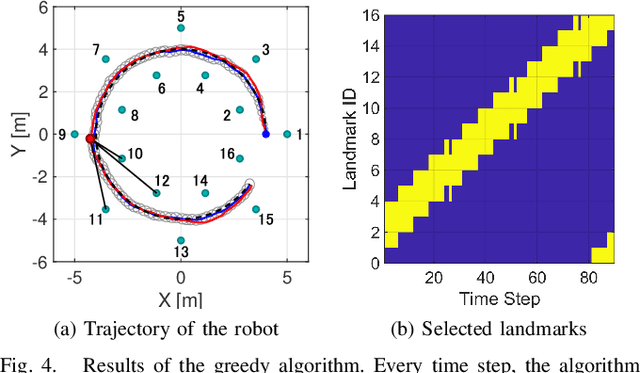
This paper considers the problem of task-dependent (top-down) attention allocation for vision-based autonomous navigation using known landmarks. Unlike the existing paradigm in which landmark selection is formulated as a combinatorial optimization problem, we model it as a resource allocation problem where the decision-maker (DM) is granted extra freedom to control the degree of attention to each landmark. The total resource available to DM is expressed in terms of the capacity limit of the in-take information flow, which is quantified by the directed information from the state of the environment to the DM's observation. We consider a receding horizon implementation of such a controlled sensing scheme in the Linear-Quadratic-Gaussian (LQG) regime. The convex-concave procedure is applied in each time step, whose time complexity is shown to be linear in the horizon length if the alternating direction method of multipliers (ADMM) is used. Numerical studies show that the proposed formulation is sparsity-promoting in the sense that it tends to allocate zero data rate to uninformative landmarks.

Closed-loop Parameter Identification of Linear Dynamical Systems through the Lens of Feedback Channel Coding Theory

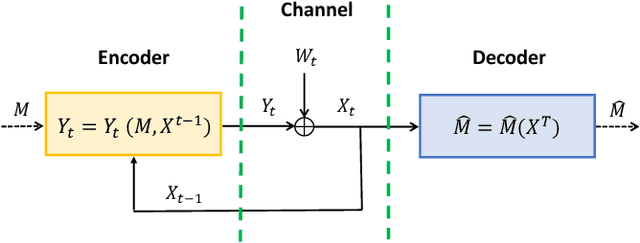
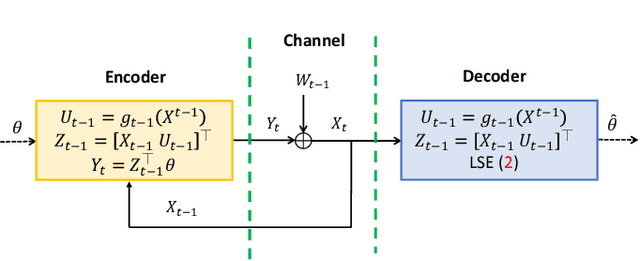
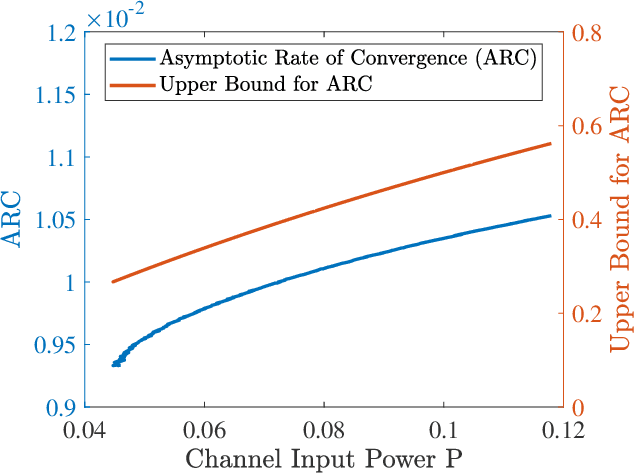
This paper considers the problem of closed-loop identification of linear scalar systems with Gaussian process noise, where the system input is determined by a deterministic state feedback policy. The regularized least-square estimate (LSE) algorithm is adopted, seeking to find the best estimate of unknown model parameters based on noiseless measurements of the state. We are interested in the fundamental limitation of the rate at which unknown parameters can be learned, in the sense of the D-optimality scalarization criterion subject to a quadratic control cost. We first establish a novel connection between a closed-loop identification problem of interest and a channel coding problem involving an additive white Gaussian noise (AWGN) channel with feedback and a certain structural constraint. Based on this connection, we show that the learning rate is fundamentally upper bounded by the capacity of the corresponding AWGN channel. Although the optimal design of the feedback policy remains challenging, we derive conditions under which the upper bound is achieved. Finally, we show that the obtained upper bound implies that super-linear convergence is unattainable for any choice of the policy.

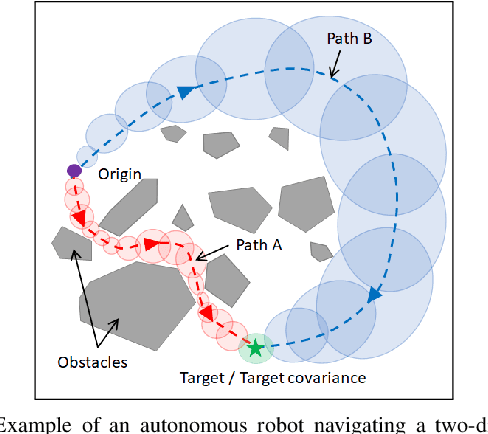
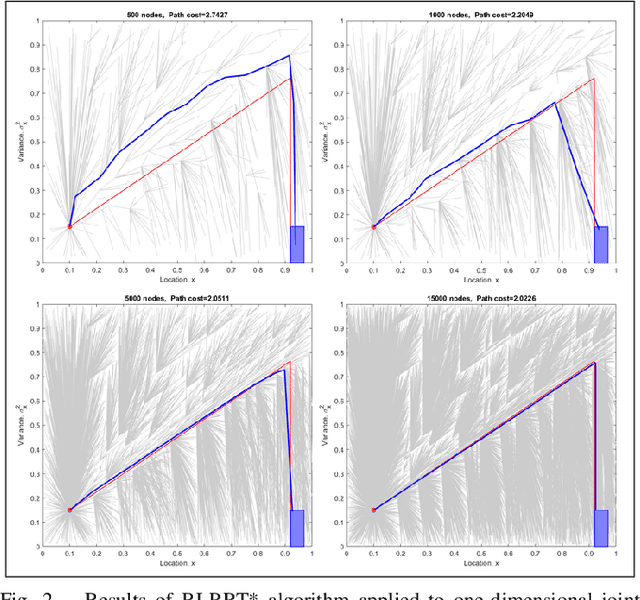
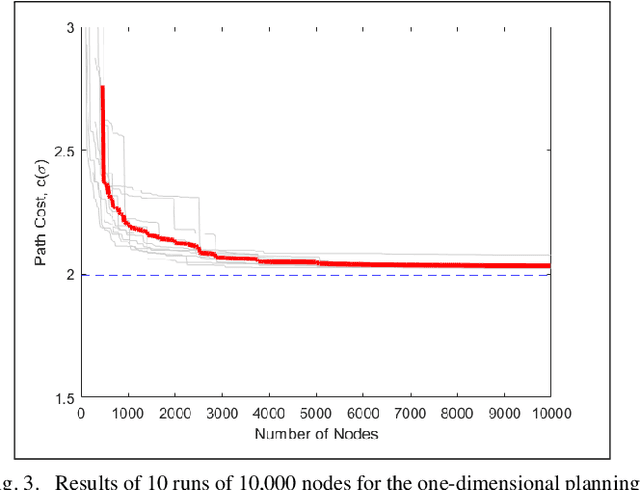
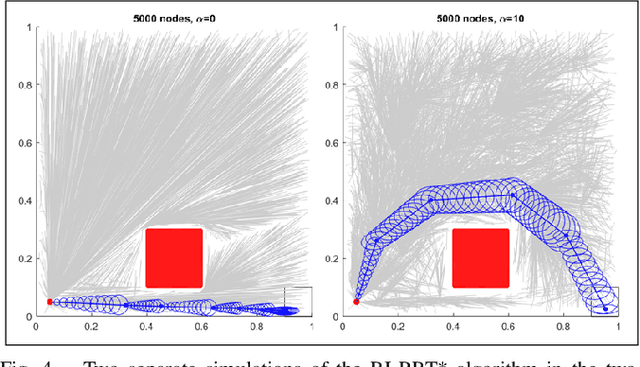
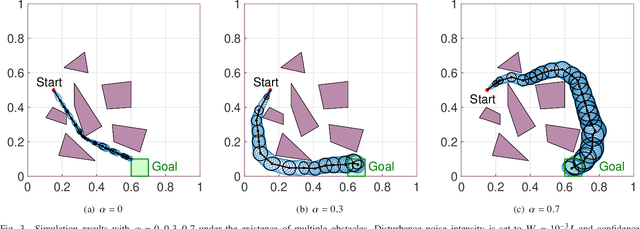
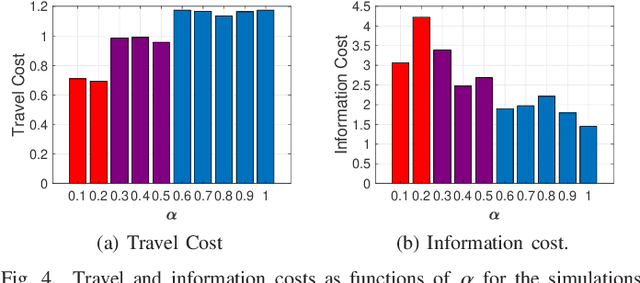
Rationally Inattentive Path-Planning via RRT*

We consider a path-planning scenario for a mobile robot traveling in a configuration space with obstacles under the presence of stochastic disturbances. A novel path length metric is proposed on the uncertain configuration space and then integrated with the existing RRT* algorithm. The metric is a weighted sum of two terms which capture both the Euclidean distance traveled by the robot and the perception cost, i.e., the amount of information the robot must perceive about the environment to follow the path safely. The continuity of the path length function with respect to the topology of the total variation metric is shown and the optimality of the Rationally Inattentive RRT* algorithm is discussed. Three numerical studies are presented which display the utility of the new algorithm.