Task Hierarchical Control via Null-Space Projection and Path Integral Approach

This paper addresses the problem of hierarchical task control, where a robotic system must perform multiple subtasks with varying levels of priority. A commonly used approach for hierarchical control is the null-space projection technique, which ensures that higher-priority tasks are executed without interference from lower-priority ones. While effective, the state-of-the-art implementations of this method rely on low-level controllers, such as PID controllers, which can be prone to suboptimal solutions in complex tasks. This paper presents a novel framework for hierarchical task control, integrating the null-space projection technique with the path integral control method. Our approach leverages Monte Carlo simulations for real-time computation of optimal control inputs, allowing for the seamless integration of simpler PID-like controllers with a more sophisticated optimal control technique. Through simulation studies, we demonstrate the effectiveness of this combined approach, showing how it overcomes the limitations of traditional

Energy-Aware Task Allocation for Teams of Multi-mode Robots

This work proposes a novel multi-robot task allocation framework for robots that can switch between multiple modes, e.g., flying, driving, or walking. We first provide a method to encode the multi-mode property of robots as a graph, where the mode of each robot is represented by a node. Next, we formulate a constrained optimization problem to decide both the task to be allocated to each robot as well as the mode in which the latter should execute the task. The robot modes are optimized based on the state of the robot and the environment, as well as the energy required to execute the allocated task. Moreover, the proposed framework is able to encompass kinematic and dynamic models of robots alike. Furthermore, we provide sufficient conditions for the convergence of task execution and allocation for both robot models.

Design and Control of a VTOL Aerial Vehicle Tilting its Rotors Only with Rotor Thrusts and a Passive Joint

This paper presents a novel VTOL UAV that owns a link connecting four rotors and a fuselage by a passive joint, allowing the control of the rotor's tilting angle by adjusting the rotors' thrust. This unique structure contributes to eliminating additional actuators, such as servo motors, to control the tilting angles of rotors, resulting in the UAV's weight lighter and simpler structure. We first derive the dynamical model of the newly designed UAV and analyze its controllability. Then, we design the controller that leverages the tiltable link with four rotors to accelerate the UAV while suppressing a deviation of the UAV's angle of attack from the desired value to restrain the change of the aerodynamic force. Finally, the validity of the proposed control strategy is evaluated in simulation study.

Collision Avoidance for Ellipsoidal Rigid Bodies with Control Barrier Functions Designed from Rotating Supporting Hyperplanes

This paper proposes a collision avoidance method for ellipsoidal rigid bodies, which utilizes a control barrier function (CBF) designed from a supporting hyperplane. We formulate the problem in the Special Euclidean Group SE(2) and SE(3), where the dynamics are described as rigid body motion (RBM). Then, we consider the condition for separating two ellipsoidal rigid bodies by employing a signed distance from a supporting hyperplane of a rigid body to the other rigid body. Although the positive value of this signed distance implies that two rigid bodies are collision-free, a naively prepared supporting hyperplane yields a smaller value than the actual distance. To avoid such a conservative evaluation, the supporting hyperplane is rotated so that the signed distance from the supporting hyperplane to the other rigid body is maximized. We prove that the maximum value of this optimization problem is equal to the actual distance between two ellipsoidal rigid bodies, hence eliminating excessive conservativeness. We leverage this signed distance as a CBF to prevent collision while the supporting hyperplane is rotated via a gradient-based input. The designed CBF is integrated into a quadratic programming (QP) problem, where each rigid body calculates its collision-free input in a distributed manner, given communication among rigid bodies. The proposed method is demonstrated with simulations. Finally, we exemplify our method can be extended to a vehicle having nonholonomic dynamics.

Gaussian Belief Space Path Planning for Minimum Sensing Navigation

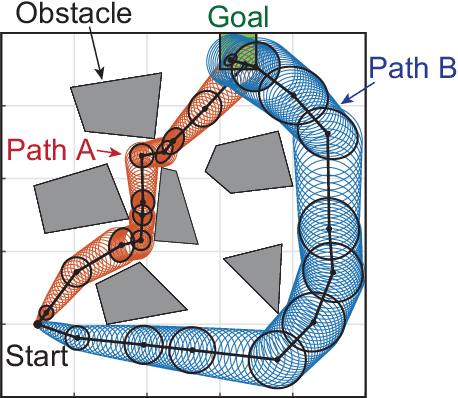
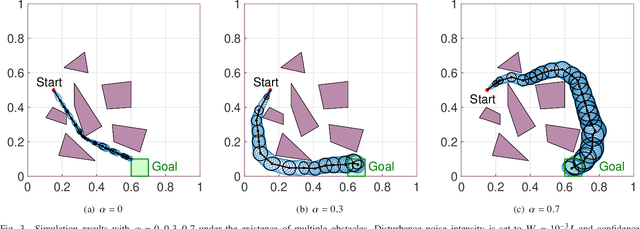
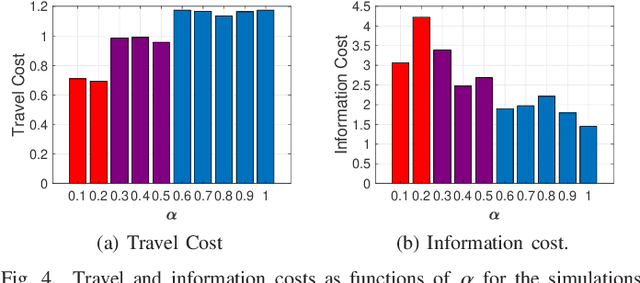
We propose a path planning methodology for a mobile robot navigating through an obstacle-filled environment to generate a reference path that is traceable with moderate sensing efforts. The desired reference path is characterized as the shortest path in an obstacle-filled Gaussian belief manifold equipped with a novel information-geometric distance function. The distance function we introduce is shown to be an asymmetric quasi-pseudometric and can be interpreted as the minimum information gain required to steer the Gaussian belief. An RRT*-based numerical solution algorithm is presented to solve the formulated shortest-path problem. To gain insight into the asymptotic optimality of the proposed algorithm, we show that the considered path length function is continuous with respect to the topology of total variation. Simulation results demonstrate that the proposed method is effective in various robot navigation scenarios to reduce sensing costs, such as the required frequency of sensor measurements and the number of sensors that must be operated simultaneously.

Dynamic Allocation of Visual Attention for Vision-based Autonomous Navigation under Data Rate Constraints

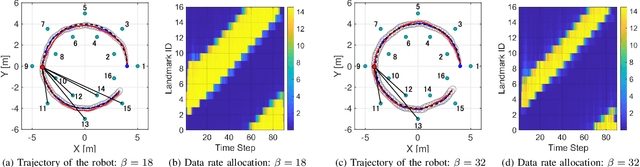
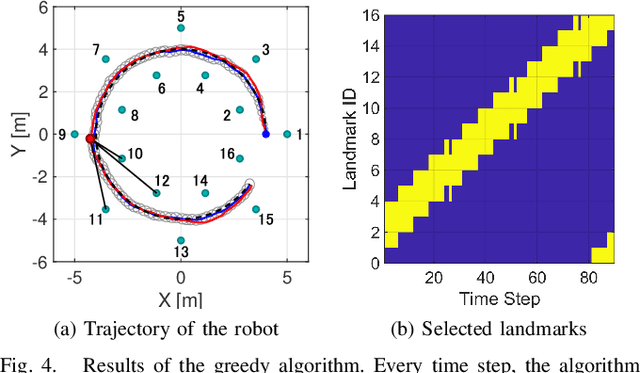
This paper considers the problem of task-dependent (top-down) attention allocation for vision-based autonomous navigation using known landmarks. Unlike the existing paradigm in which landmark selection is formulated as a combinatorial optimization problem, we model it as a resource allocation problem where the decision-maker (DM) is granted extra freedom to control the degree of attention to each landmark. The total resource available to DM is expressed in terms of the capacity limit of the in-take information flow, which is quantified by the directed information from the state of the environment to the DM's observation. We consider a receding horizon implementation of such a controlled sensing scheme in the Linear-Quadratic-Gaussian (LQG) regime. The convex-concave procedure is applied in each time step, whose time complexity is shown to be linear in the horizon length if the alternating direction method of multipliers (ADMM) is used. Numerical studies show that the proposed formulation is sparsity-promoting in the sense that it tends to allocate zero data rate to uninformative landmarks.

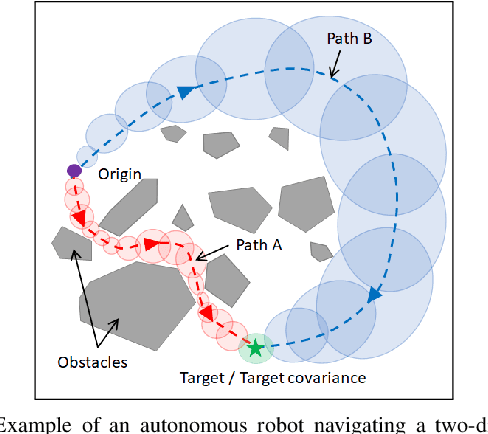
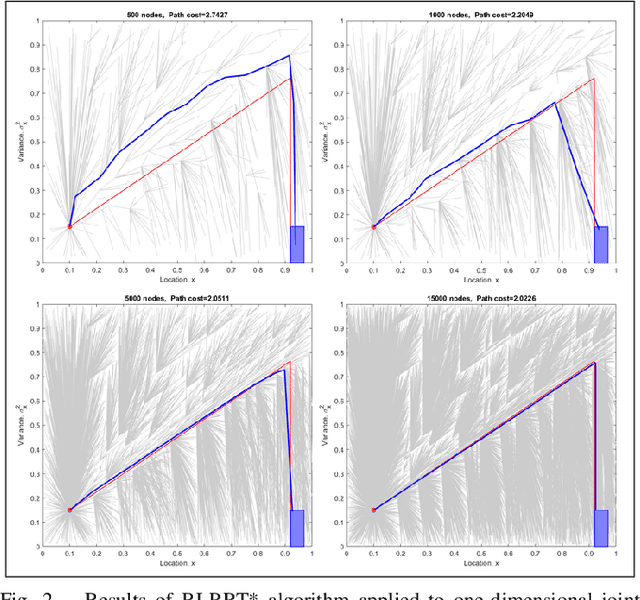
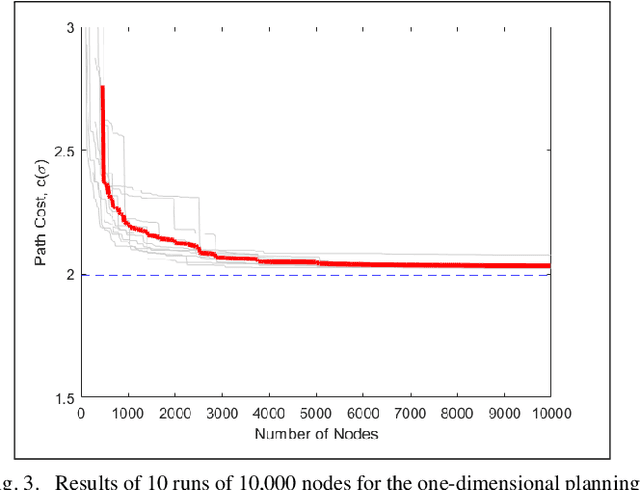
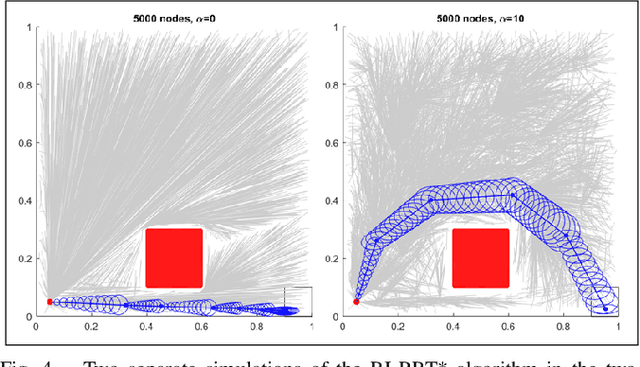
Rationally Inattentive Path-Planning via RRT*

We consider a path-planning scenario for a mobile robot traveling in a configuration space with obstacles under the presence of stochastic disturbances. A novel path length metric is proposed on the uncertain configuration space and then integrated with the existing RRT* algorithm. The metric is a weighted sum of two terms which capture both the Euclidean distance traveled by the robot and the perception cost, i.e., the amount of information the robot must perceive about the environment to follow the path safely. The continuity of the path length function with respect to the topology of the total variation metric is shown and the optimality of the Rationally Inattentive RRT* algorithm is discussed. Three numerical studies are presented which display the utility of the new algorithm.