Task Hierarchical Control via Null-Space Projection and Path Integral Approach

This paper addresses the problem of hierarchical task control, where a robotic system must perform multiple subtasks with varying levels of priority. A commonly used approach for hierarchical control is the null-space projection technique, which ensures that higher-priority tasks are executed without interference from lower-priority ones. While effective, the state-of-the-art implementations of this method rely on low-level controllers, such as PID controllers, which can be prone to suboptimal solutions in complex tasks. This paper presents a novel framework for hierarchical task control, integrating the null-space projection technique with the path integral control method. Our approach leverages Monte Carlo simulations for real-time computation of optimal control inputs, allowing for the seamless integration of simpler PID-like controllers with a more sophisticated optimal control technique. Through simulation studies, we demonstrate the effectiveness of this combined approach, showing how it overcomes the limitations of traditional

Upper Bounds for Continuous-Time End-to-End Risks in Stochastic Robot Navigation

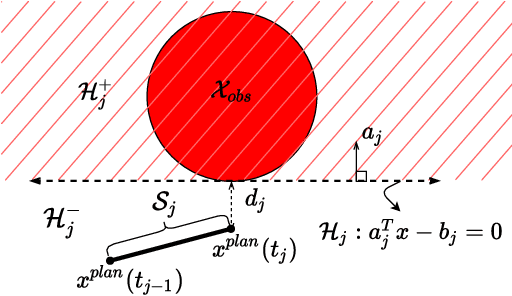
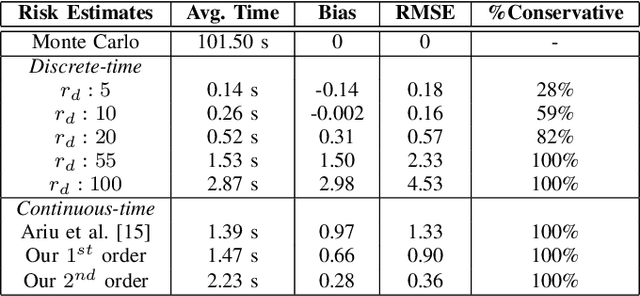
We present an analytical method to estimate the continuous-time collision probability of motion plans for autonomous agents with linear controlled Ito dynamics. Motion plans generated by planning algorithms cannot be perfectly executed by autonomous agents in reality due to the inherent uncertainties in the real world. Estimating end-to-end risk is crucial to characterize the safety of trajectories and plan risk optimal trajectories. In this paper, we derive upper bounds for the continuous-time risk in stochastic robot navigation using the properties of Brownian motion as well as Boole and Hunter's inequalities from probability theory. Using a ground robot navigation example, we numerically demonstrate that our method is considerably faster than the naive Monte Carlo sampling method and the proposed bounds perform better than the discrete-time risk bounds.

Chance-Constrained Stochastic Optimal Control via Path Integral and Finite Difference Methods

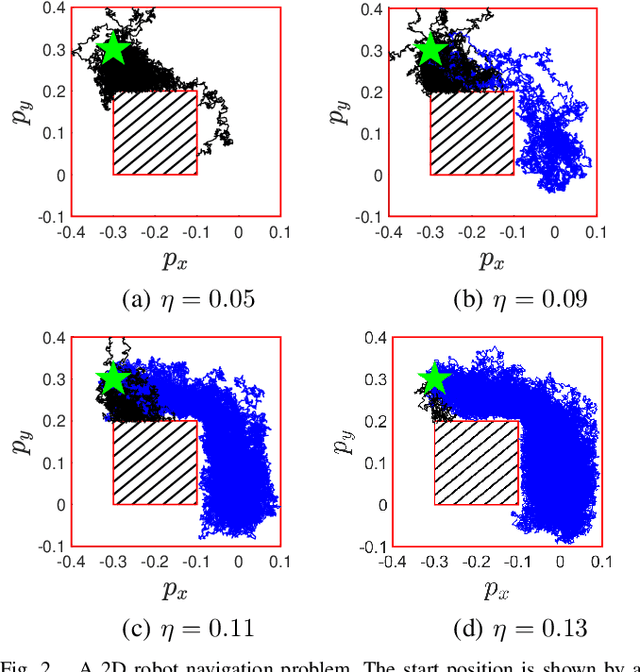
This paper addresses a continuous-time continuous-space chance-constrained stochastic optimal control (SOC) problem via a Hamilton-Jacobi-Bellman (HJB) partial differential equation (PDE). Through Lagrangian relaxation, we convert the chance-constrained (risk-constrained) SOC problem to a risk-minimizing SOC problem, the cost function of which possesses the time-additive Bellman structure. We show that the risk-minimizing control synthesis is equivalent to solving an HJB PDE whose boundary condition can be tuned appropriately to achieve a desired level of safety. Furthermore, it is shown that the proposed risk-minimizing control problem can be viewed as a generalization of the problem of estimating the risk associated with a given control policy. Two numerical techniques are explored, namely the path integral and the finite difference method (FDM), to solve a class of risk-minimizing SOC problems whose associated HJB equation is linearizable via the Cole-Hopf transformation. Using a 2D robot navigation example, we validate the proposed control synthesis framework and compare the solutions obtained using path integral and FDM.

Upper and Lower Bounds for End-to-End Risks in Stochastic Robot Navigation

We present novel upper and lower bounds to estimate the collision probability of motion plans for autonomous agents with discrete-time linear Gaussian dynamics. Motion plans generated by planning algorithms cannot be perfectly executed by autonomous agents in reality due to the inherent uncertainties in the real world. Estimating collision probability is crucial to characterize the safety of trajectories and plan risk optimal trajectories. Our approach is an application of standard results in probability theory including the inequalities of Hunter, Kounias, Frechet, and Dawson. Using a ground robot navigation example, we numerically demonstrate that our method is considerably faster than the naive Monte Carlo sampling method and the proposed bounds are significantly less conservative than Boole's bound commonly used in the literature.