Efficient Implementation of Reinforcement Learning over Homomorphic Encryption

We investigate encrypted control policy synthesis over the cloud. While encrypted control implementations have been studied previously, we focus on the less explored paradigm of privacy-preserving control synthesis, which can involve heavier computations ideal for cloud outsourcing. We classify control policy synthesis into model-based, simulator-driven, and data-driven approaches and examine their implementation over fully homomorphic encryption (FHE) for privacy enhancements. A key challenge arises from comparison operations (min or max) in standard reinforcement learning algorithms, which are difficult to execute over encrypted data. This observation motivates our focus on Relative-Entropy-regularized reinforcement learning (RL) problems, which simplifies encrypted evaluation of synthesis algorithms due to their comparison-free structures. We demonstrate how linearly solvable value iteration, path integral control, and Z-learning can be readily implemented over FHE. We conduct a case study of our approach through numerical simulations of encrypted Z-learning in a grid world environment using the CKKS encryption scheme, showing convergence with acceptable approximation error. Our work suggests the potential for secure and efficient cloud-based reinforcement learning.

Task Hierarchical Control via Null-Space Projection and Path Integral Approach

This paper addresses the problem of hierarchical task control, where a robotic system must perform multiple subtasks with varying levels of priority. A commonly used approach for hierarchical control is the null-space projection technique, which ensures that higher-priority tasks are executed without interference from lower-priority ones. While effective, the state-of-the-art implementations of this method rely on low-level controllers, such as PID controllers, which can be prone to suboptimal solutions in complex tasks. This paper presents a novel framework for hierarchical task control, integrating the null-space projection technique with the path integral control method. Our approach leverages Monte Carlo simulations for real-time computation of optimal control inputs, allowing for the seamless integration of simpler PID-like controllers with a more sophisticated optimal control technique. Through simulation studies, we demonstrate the effectiveness of this combined approach, showing how it overcomes the limitations of traditional

Randomized Greedy Methods for Weak Submodular Sensor Selection with Robustness Considerations

We study a pair of budget- and performance-constrained weak submodular maximization problems. For computational efficiency, we explore the use of stochastic greedy algorithms which limit the search space via random sampling instead of the standard greedy procedure which explores the entire feasible search space. We propose a pair of stochastic greedy algorithms, namely, Modified Randomized Greedy (MRG) and Dual Randomized Greedy (DRG) to approximately solve the budget- and performance-constrained problems, respectively. For both algorithms, we derive approximation guarantees that hold with high probability. We then examine the use of DRG in robust optimization problems wherein the objective is to maximize the worst-case of a number of weak submodular objectives and propose the Randomized Weak Submodular Saturation Algorithm (Random-WSSA). We further derive a high-probability guarantee for when Random-WSSA successfully constructs a robust solution. Finally, we showcase the effectiveness of these algorithms in a variety of relevant uses within the context of Earth-observing LEO constellations which estimate atmospheric weather conditions and provide Earth coverage.

Optimal Sampling-based Motion Planning in Gaussian Belief Space for Minimum Sensing Navigation

In this paper, we consider the motion planning problem in Gaussian belief space for minimum sensing navigation. Despite the extensive use of sampling-based algorithms and their rigorous analysis in the deterministic setting, there has been little formal analysis of the quality of their solutions returned by sampling algorithms in Gaussian belief space. This paper aims to address this lack of research by examining the asymptotic behavior of the cost of solutions obtained from Gaussian belief space based sampling algorithms as the number of samples increases. To that end, we propose a sampling based motion planning algorithm termed Information Geometric PRM* (IG-PRM*) for generating feasible paths that minimize a weighted sum of the Euclidean and an information-theoretic cost and show that the cost of the solution that is returned is guaranteed to approach the global optimum in the limit of large number of samples. Finally, we consider an obstacle-free scenario and compute the optimal solution using the "move and sense" strategy in literature. We then verify that the cost returned by our proposed algorithm converges to this optimal solution as the number of samples increases.

Online variable-length source coding for minimum bitrate LQG control

We propose an adaptive coding approach to achieve linear-quadratic-Gaussian (LQG) control with near-minimum bitrate prefix-free feedback. Our approach combines a recent analysis of a quantizer design for minimum rate LQG control with work on universal lossless source coding for sources on countable alphabets. In the aforementioned quantizer design, it was established that the quantizer outputs are an asymptotically stationary, ergodic process. To enable LQG control with provably near-minimum bitrate, the quantizer outputs must be encoded into binary codewords efficiently. This is possible given knowledge of the probability distributions of the quantizer outputs, or of their limiting distribution. Obtaining such knowledge is challenging; the distributions do not readily admit closed form descriptions. This motivates the application of universal source coding. Our main theoretical contribution in this work is a proof that (after an invertible transformation), the quantizer outputs are random variables that fall within an exponential or power-law envelope class (depending on the plant dimension). Using ideas from universal coding on envelope classes, we develop a practical, zero-delay version of these algorithms that operates with fixed precision arithmetic. We evaluate the performance of this algorithm numerically, and demonstrate competitive results with respect to fundamental tradeoffs between bitrate and LQG control performance.

A Smoothing Algorithm for Minimum Sensing Path Plans in Gaussian Belief Space

This paper explores minimum sensing navigation of robots in environments cluttered with obstacles. The general objective is to find a path plan to a goal region that requires minimal sensing effort. In [1], the information-geometric RRT* (IG-RRT*) algorithm was proposed to efficiently find such a path. However, like any stochastic sampling-based planner, the computational complexity of IG-RRT* grows quickly, impeding its use with a large number of nodes. To remedy this limitation, we suggest running IG-RRT* with a moderate number of nodes, and then using a smoothing algorithm to adjust the path obtained. To develop a smoothing algorithm, we explicitly formulate the minimum sensing path planning problem as an optimization problem. For this formulation, we introduce a new safety constraint to impose a bound on the probability of collision with obstacles in continuous-time, in contrast to the common discrete-time approach. The problem is amenable to solution via the convex-concave procedure (CCP). We develop a CCP algorithm for the formulated optimization and use this algorithm for path smoothing. We demonstrate the efficacy of the proposed approach through numerical simulations.

Time-invariant prefix-free source coding for MIMO LQG control

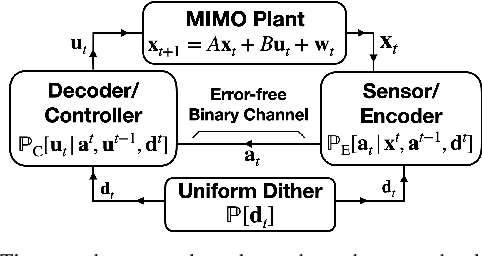
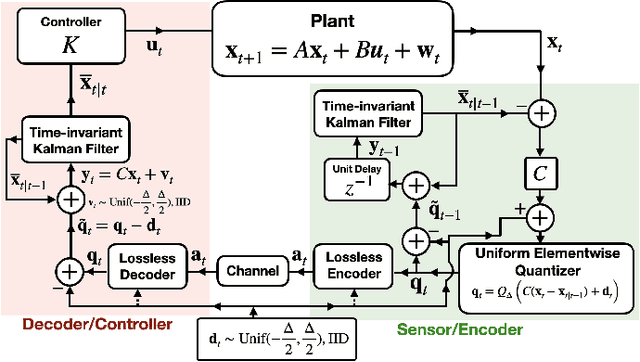
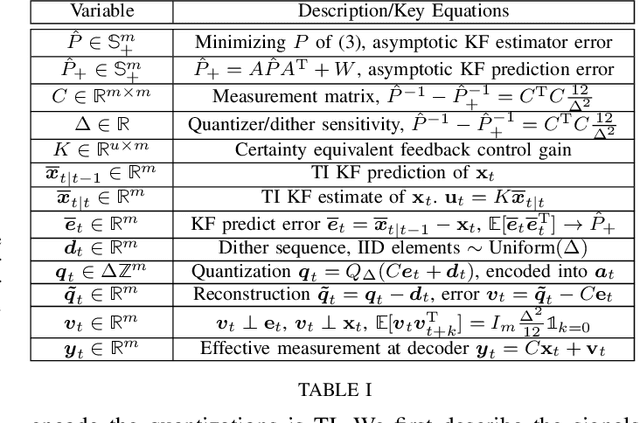
In this work we consider discrete-time multiple-input multiple-output (MIMO) linear-quadratic-Gaussian (LQG) control where the feedback consists of variable length binary codewords. To simplify the decoder architecture, we enforce a strict prefix constraint on the codewords. We develop a data compression architecture that provably achieves a near minimum time-average expected bitrate for a fixed constraint on the LQG performance. The architecture conforms to the strict prefix constraint and does not require time-varying lossless source coding, in contrast to the prior art.

Upper Bounds for Continuous-Time End-to-End Risks in Stochastic Robot Navigation

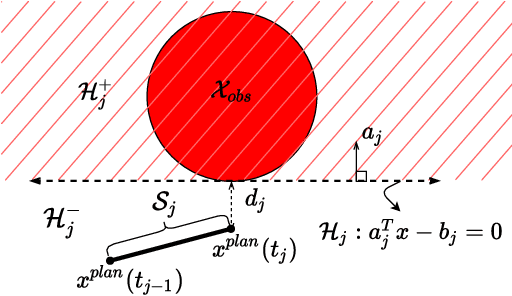
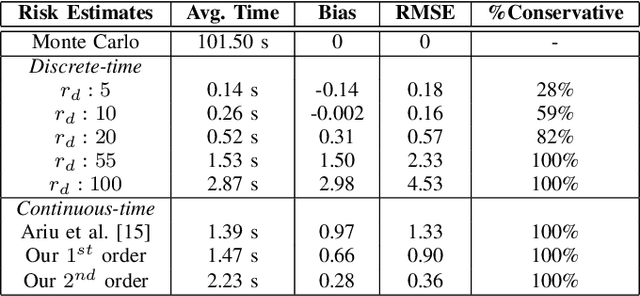
We present an analytical method to estimate the continuous-time collision probability of motion plans for autonomous agents with linear controlled Ito dynamics. Motion plans generated by planning algorithms cannot be perfectly executed by autonomous agents in reality due to the inherent uncertainties in the real world. Estimating end-to-end risk is crucial to characterize the safety of trajectories and plan risk optimal trajectories. In this paper, we derive upper bounds for the continuous-time risk in stochastic robot navigation using the properties of Brownian motion as well as Boole and Hunter's inequalities from probability theory. Using a ground robot navigation example, we numerically demonstrate that our method is considerably faster than the naive Monte Carlo sampling method and the proposed bounds perform better than the discrete-time risk bounds.

Chance-Constrained Stochastic Optimal Control via Path Integral and Finite Difference Methods

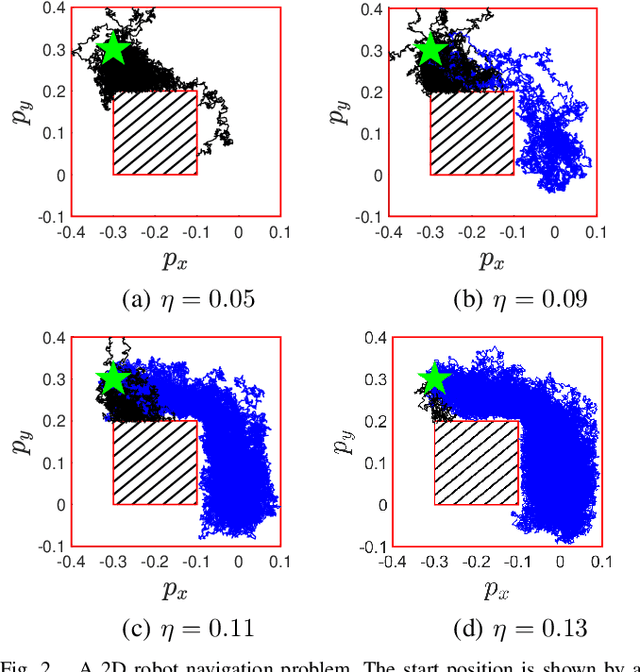
This paper addresses a continuous-time continuous-space chance-constrained stochastic optimal control (SOC) problem via a Hamilton-Jacobi-Bellman (HJB) partial differential equation (PDE). Through Lagrangian relaxation, we convert the chance-constrained (risk-constrained) SOC problem to a risk-minimizing SOC problem, the cost function of which possesses the time-additive Bellman structure. We show that the risk-minimizing control synthesis is equivalent to solving an HJB PDE whose boundary condition can be tuned appropriately to achieve a desired level of safety. Furthermore, it is shown that the proposed risk-minimizing control problem can be viewed as a generalization of the problem of estimating the risk associated with a given control policy. Two numerical techniques are explored, namely the path integral and the finite difference method (FDM), to solve a class of risk-minimizing SOC problems whose associated HJB equation is linearizable via the Cole-Hopf transformation. Using a 2D robot navigation example, we validate the proposed control synthesis framework and compare the solutions obtained using path integral and FDM.

Prefix-Free Coding for LQG Control

In this work, we develop quantization and variable-length source codecs for the feedback links in linear-quadratic-Gaussian (LQG) control systems. We prove that for any fixed control performance, the approaches we propose nearly achieve lower bounds on communication cost that have been established in prior work. In particular, we refine the analysis of a classical achievability approach with an eye towards more practical details. Notably, in the prior literature the source codecs used to demonstrate the (near) achievability of these lower bounds are often implicitly assumed to be time-varying. For single-input single-output (SISO) plants, we prove that it suffices to consider time-invariant quantization and source coding. This result follows from analyzing the long-term stochastic behavior of the system's quantized measurements and reconstruction errors. To our knowledge, this time-invariant achievability result is the first in the literature.