Online variable-length source coding for minimum bitrate LQG control

We propose an adaptive coding approach to achieve linear-quadratic-Gaussian (LQG) control with near-minimum bitrate prefix-free feedback. Our approach combines a recent analysis of a quantizer design for minimum rate LQG control with work on universal lossless source coding for sources on countable alphabets. In the aforementioned quantizer design, it was established that the quantizer outputs are an asymptotically stationary, ergodic process. To enable LQG control with provably near-minimum bitrate, the quantizer outputs must be encoded into binary codewords efficiently. This is possible given knowledge of the probability distributions of the quantizer outputs, or of their limiting distribution. Obtaining such knowledge is challenging; the distributions do not readily admit closed form descriptions. This motivates the application of universal source coding. Our main theoretical contribution in this work is a proof that (after an invertible transformation), the quantizer outputs are random variables that fall within an exponential or power-law envelope class (depending on the plant dimension). Using ideas from universal coding on envelope classes, we develop a practical, zero-delay version of these algorithms that operates with fixed precision arithmetic. We evaluate the performance of this algorithm numerically, and demonstrate competitive results with respect to fundamental tradeoffs between bitrate and LQG control performance.

Time-invariant prefix-free source coding for MIMO LQG control

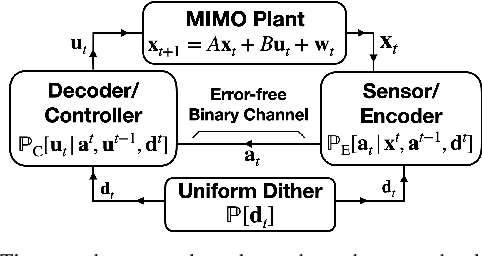
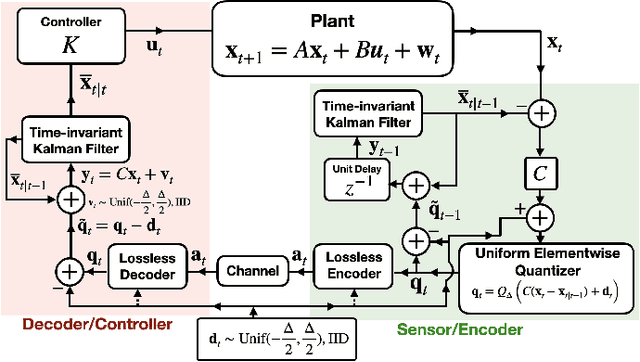
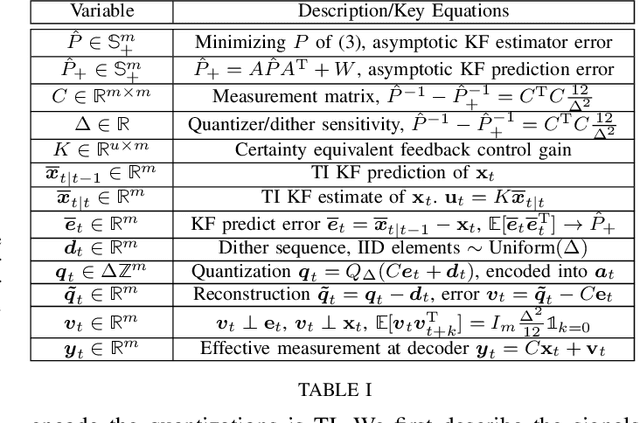
In this work we consider discrete-time multiple-input multiple-output (MIMO) linear-quadratic-Gaussian (LQG) control where the feedback consists of variable length binary codewords. To simplify the decoder architecture, we enforce a strict prefix constraint on the codewords. We develop a data compression architecture that provably achieves a near minimum time-average expected bitrate for a fixed constraint on the LQG performance. The architecture conforms to the strict prefix constraint and does not require time-varying lossless source coding, in contrast to the prior art.

A Lower-bound for Variable-length Source Coding in LQG Feedback Control

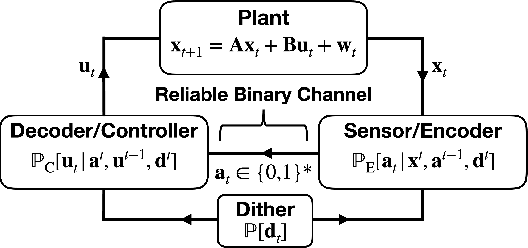
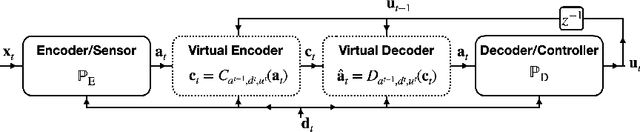
In this letter, we consider a Linear Quadratic Gaussian (LQG) control system where feedback occurs over a noiseless binary channel and derive lower bounds on the minimum communication cost (quantified via the channel bitrate) required to attain a given control performance. We assume that at every time step an encoder can convey a packet containing a variable number of bits over the channel to a decoder at the controller. Our system model provides for the possibility that the encoder and decoder have shared randomness, as is the case in systems using dithered quantizers. We define two extremal prefix-free requirements that may be imposed on the message packets; such constraints are useful in that they allow the decoder, and potentially other agents to uniquely identify the end of a transmission in an online fashion. We then derive a lower bound on the rate of prefix-free coding in terms of directed information; in particular we show that a previously known bound still holds in the case with shared randomness. We also provide a generalization of the bound that applies if prefix-free requirements are relaxed. We conclude with a rate-distortion formulation.

Rate of Prefix-free Codes in LQG Control Systems with Side Information

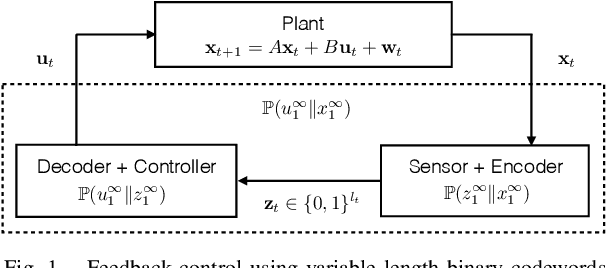
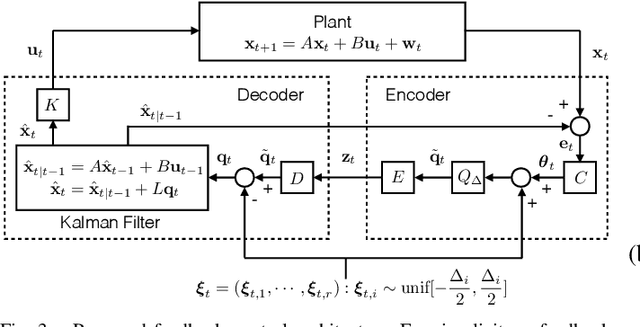
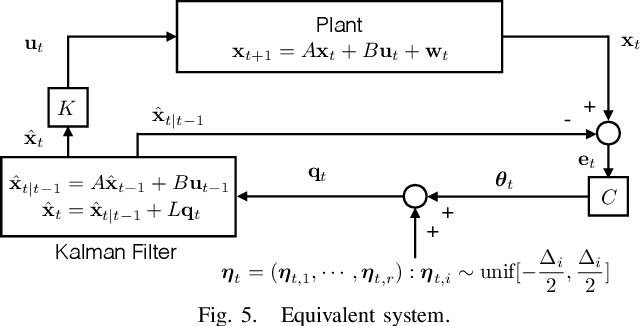
In this work, we study an LQG control system where one of two feedback channels is discrete and incurs a communication cost. We assume that a decoder (co-located with the controller) can make noiseless measurements of a subset of the state vector (referred to as side information) meanwhile a remote encoder (co-located with a sensor) can make arbitrary measurements of the entire state vector, but must convey its measurements to the decoder over a noiseless binary channel. Use of the channel incurs a communication cost, quantified as the time-averaged expected length of prefix-free binary codeword. We study the tradeoff between the communication cost and control performance. The formulation motivates a constrained directed information minimization problem, which can be solved via convex optimization. Using the optimization, we propose a quantizer design and a subsequent achievability result.