Distributed Shape Learning of Complex Objects Using Gaussian Kernel

This paper addresses distributed learning of a complex object for multiple networked robots based on distributed optimization and kernel-based support vector machine. In order to overcome a fundamental limitation of polynomial kernels assumed in our antecessor, we employ Gaussian kernel as a kernel function for classification. The Gaussian kernel prohibits the robots to share the function through a finite number of equality constraints due to its infinite dimensionality of the function space. We thus reformulate the optimization problem assuming that the target function space is identified with the space spanned by the bases associated with not the data but a finite number of grid points. The above relaxation is shown to allow the robots to share the function by a finite number of equality constraints. We finally demonstrate the present approach through numerical simulations.

Collision Avoidance for Ellipsoidal Rigid Bodies with Control Barrier Functions Designed from Rotating Supporting Hyperplanes

This paper proposes a collision avoidance method for ellipsoidal rigid bodies, which utilizes a control barrier function (CBF) designed from a supporting hyperplane. We formulate the problem in the Special Euclidean Group SE(2) and SE(3), where the dynamics are described as rigid body motion (RBM). Then, we consider the condition for separating two ellipsoidal rigid bodies by employing a signed distance from a supporting hyperplane of a rigid body to the other rigid body. Although the positive value of this signed distance implies that two rigid bodies are collision-free, a naively prepared supporting hyperplane yields a smaller value than the actual distance. To avoid such a conservative evaluation, the supporting hyperplane is rotated so that the signed distance from the supporting hyperplane to the other rigid body is maximized. We prove that the maximum value of this optimization problem is equal to the actual distance between two ellipsoidal rigid bodies, hence eliminating excessive conservativeness. We leverage this signed distance as a CBF to prevent collision while the supporting hyperplane is rotated via a gradient-based input. The designed CBF is integrated into a quadratic programming (QP) problem, where each rigid body calculates its collision-free input in a distributed manner, given communication among rigid bodies. The proposed method is demonstrated with simulations. Finally, we exemplify our method can be extended to a vehicle having nonholonomic dynamics.

Gaussian Control Barrier Functions : A Non-Parametric Paradigm to Safety

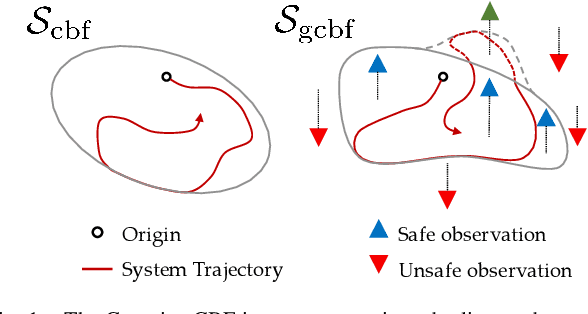
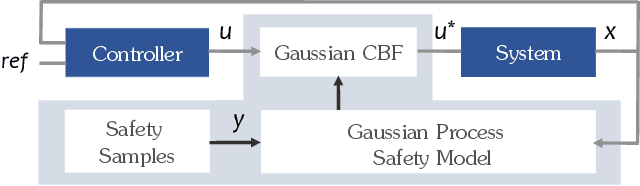
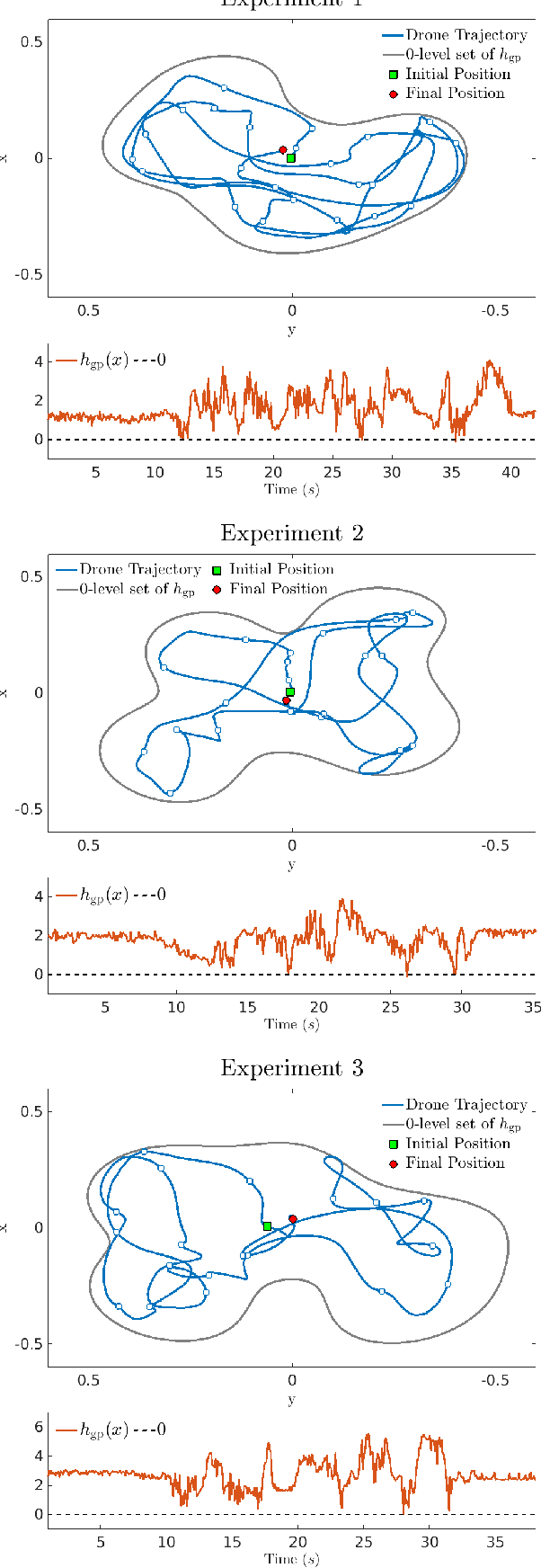
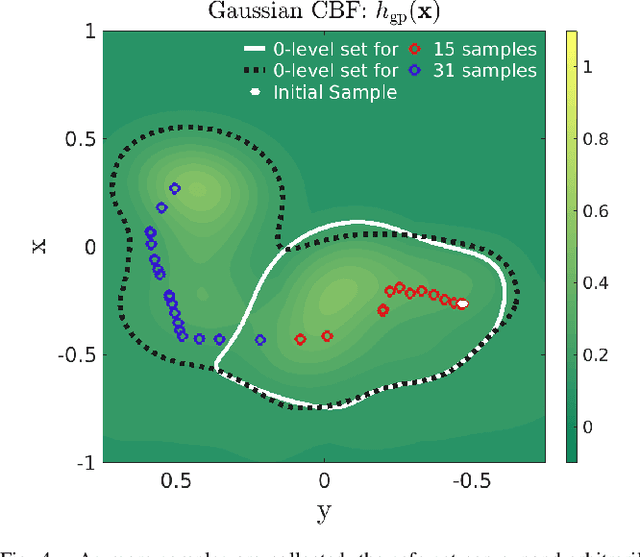
Inspired by the success of control barrier functions (CBFs) in addressing safety, and the rise of data-driven techniques for modeling functions, we propose a non-parametric approach for online synthesis of CBFs using Gaussian Processes (GPs). Mathematical constructs such as CBFs have achieved safety by designing a candidate function a priori. However, designing such a candidate function can be challenging. A practical example of such a setting would be to design a CBF in a disaster recovery scenario where safe and navigable regions need to be determined. The decision boundary for safety in such an example is unknown and cannot be designed a priori. In our approach, we work with safety samples or observations to construct the CBF online by assuming a flexible GP prior on these samples, and term our formulation as a Gaussian CBF. GPs have favorable properties, in addition to being non-parametric, such as analytical tractability and robust uncertainty estimation. This allows realizing the posterior components with high safety guarantees by incorporating variance estimation, while also computing associated partial derivatives in closed-form to achieve safe control. Moreover, the synthesized safety function from our approach allows changing the corresponding safe set arbitrarily based on the data, thus allowing non-convex safe sets. We validate our approach experimentally on a quadrotor by demonstrating safe control for fixed but arbitrary safe sets and collision avoidance where the safe set is constructed online. Finally, we juxtapose Gaussian CBFs with regular CBFs in the presence of noisy states to highlight its flexibility and robustness to noise. The experiment video can be seen at: https://youtu.be/HX6uokvCiGk