RESOLVE: Relational Reasoning with Symbolic and Object-Level Features Using Vector Symbolic Processing

Modern transformer-based encoder-decoder architectures struggle with reasoning tasks due to their inability to effectively extract relational information between input objects (data/tokens). Recent work introduced the Abstractor module, embedded between transformer layers, to address this gap. However, the Abstractor layer while excelling at capturing relational information (pure relational reasoning), faces challenges in tasks that require both object and relational-level reasoning (partial relational reasoning). To address this, we propose RESOLVE, a neuro-vector symbolic architecture that combines object-level features with relational representations in high-dimensional spaces, using fast and efficient operations such as bundling (summation) and binding (Hadamard product) allowing both object-level features and relational representations to coexist within the same structure without interfering with one another. RESOLVE is driven by a novel attention mechanism that operates in a bipolar high dimensional space, allowing fast attention score computation compared to the state-of-the-art. By leveraging this design, the model achieves both low compute latency and memory efficiency. RESOLVE also offers better generalizability while achieving higher accuracy in purely relational reasoning tasks such as sorting as well as partial relational reasoning tasks such as math problem-solving compared to state-of-the-art methods.

LARS-VSA: A Vector Symbolic Architecture For Learning with Abstract Rules

Human cognition excels at symbolic reasoning, deducing abstract rules from limited samples. This has been explained using symbolic and connectionist approaches, inspiring the development of a neuro-symbolic architecture that combines both paradigms. In parallel, recent studies have proposed the use of a "relational bottleneck" that separates object-level features from abstract rules, allowing learning from limited amounts of data . While powerful, it is vulnerable to the curse of compositionality meaning that object representations with similar features tend to interfere with each other. In this paper, we leverage hyperdimensional computing, which is inherently robust to such interference to build a compositional architecture. We adapt the "relational bottleneck" strategy to a high-dimensional space, incorporating explicit vector binding operations between symbols and relational representations. Additionally, we design a novel high-dimensional attention mechanism that leverages this relational representation. Our system benefits from the low overhead of operations in hyperdimensional space, making it significantly more efficient than the state of the art when evaluated on a variety of test datasets, while maintaining higher or equal accuracy.

A Novel Hyperdimensional Computing Framework for Online Time Series Forecasting on the Edge

In recent years, both online and offline deep learning models have been developed for time series forecasting. However, offline deep forecasting models fail to adapt effectively to changes in time-series data, while online deep forecasting models are often expensive and have complex training procedures. In this paper, we reframe the online nonlinear time-series forecasting problem as one of linear hyperdimensional time-series forecasting. Nonlinear low-dimensional time-series data is mapped to high-dimensional (hyperdimensional) spaces for linear hyperdimensional prediction, allowing fast, efficient and lightweight online time-series forecasting. Our framework, TSF-HD, adapts to time-series distribution shifts using a novel co-training framework for its hyperdimensional mapping and its linear hyperdimensional predictor. TSF-HD is shown to outperform the state of the art, while having reduced inference latency, for both short-term and long-term time series forecasting. Our code is publicly available at http://github.com/tsfhd2024/tsf-hd.git

Gaussian Control Barrier Functions : A Non-Parametric Paradigm to Safety

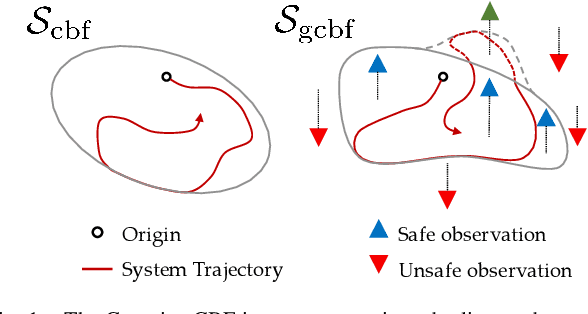
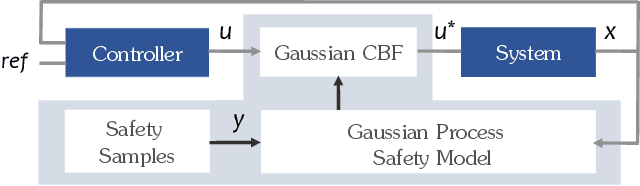
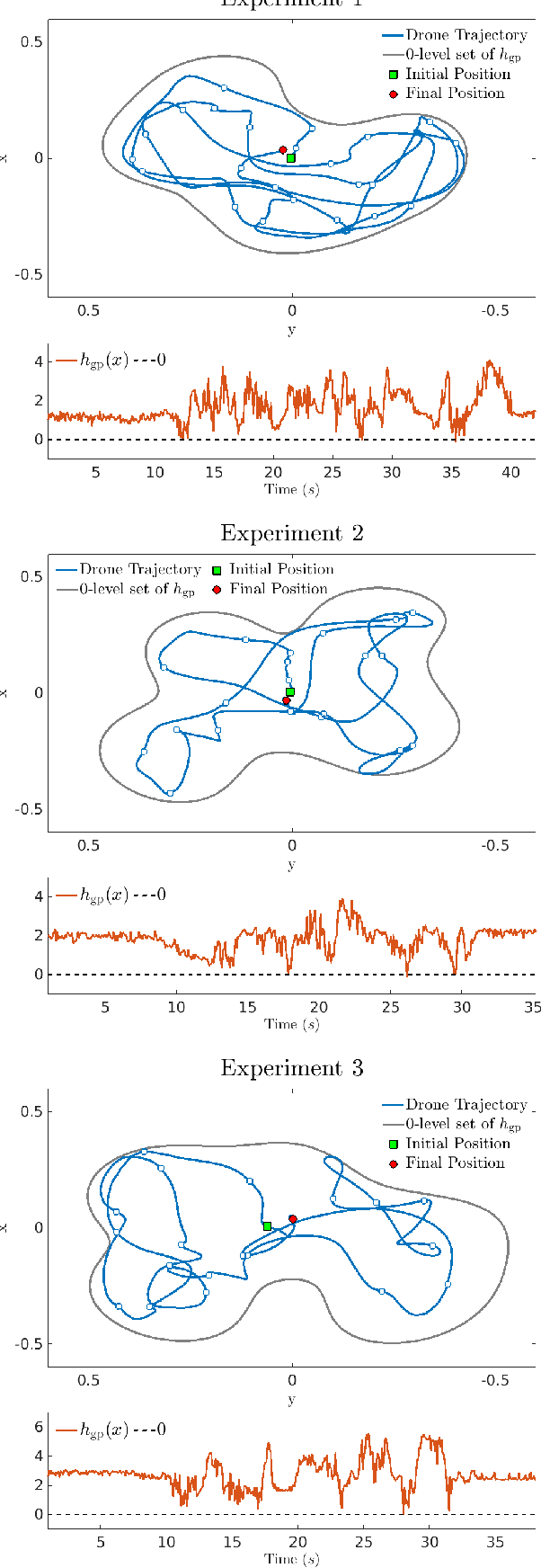
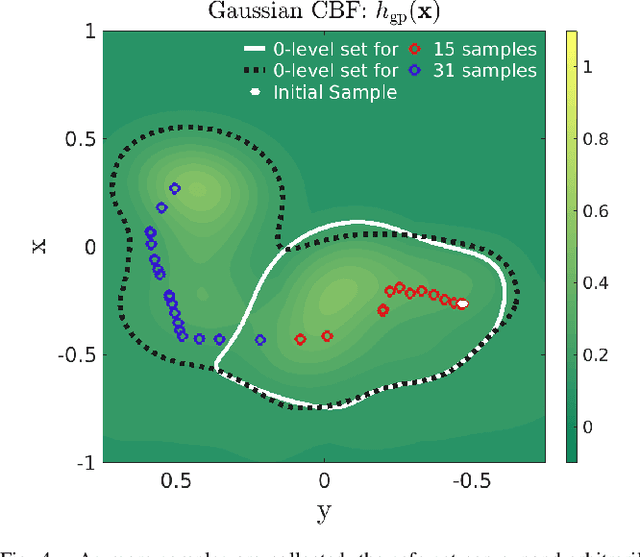
Inspired by the success of control barrier functions (CBFs) in addressing safety, and the rise of data-driven techniques for modeling functions, we propose a non-parametric approach for online synthesis of CBFs using Gaussian Processes (GPs). Mathematical constructs such as CBFs have achieved safety by designing a candidate function a priori. However, designing such a candidate function can be challenging. A practical example of such a setting would be to design a CBF in a disaster recovery scenario where safe and navigable regions need to be determined. The decision boundary for safety in such an example is unknown and cannot be designed a priori. In our approach, we work with safety samples or observations to construct the CBF online by assuming a flexible GP prior on these samples, and term our formulation as a Gaussian CBF. GPs have favorable properties, in addition to being non-parametric, such as analytical tractability and robust uncertainty estimation. This allows realizing the posterior components with high safety guarantees by incorporating variance estimation, while also computing associated partial derivatives in closed-form to achieve safe control. Moreover, the synthesized safety function from our approach allows changing the corresponding safe set arbitrarily based on the data, thus allowing non-convex safe sets. We validate our approach experimentally on a quadrotor by demonstrating safe control for fixed but arbitrary safe sets and collision avoidance where the safe set is constructed online. Finally, we juxtapose Gaussian CBFs with regular CBFs in the presence of noisy states to highlight its flexibility and robustness to noise. The experiment video can be seen at: https://youtu.be/HX6uokvCiGk

TESDA: Transform Enabled Statistical Detection of Attacks in Deep Neural Networks

Deep neural networks (DNNs) are now the de facto choice for computer vision tasks such as image classification. However, their complexity and "black box" nature often renders the systems they're deployed in vulnerable to a range of security threats. Successfully identifying such threats, especially in safety-critical real-world applications is thus of utmost importance, but still very much an open problem. We present TESDA, a low-overhead, flexible, and statistically grounded method for {online detection} of attacks by exploiting the discrepancies they cause in the distributions of intermediate layer features of DNNs. Unlike most prior work, we require neither dedicated hardware to run in real-time, nor the presence of a Trojan trigger to detect discrepancies in behavior. We empirically establish our method's usefulness and practicality across multiple architectures, datasets and diverse attacks, consistently achieving detection coverages of above 95% with operation count overheads as low as 1-2%.

Multi-Sparse Gaussian Process: Learning based Semi-Parametric Control

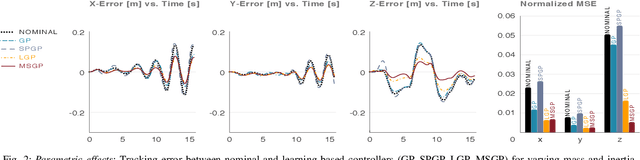
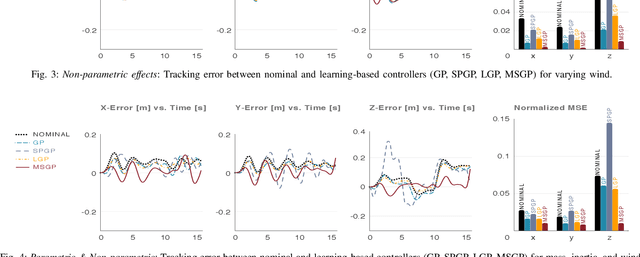
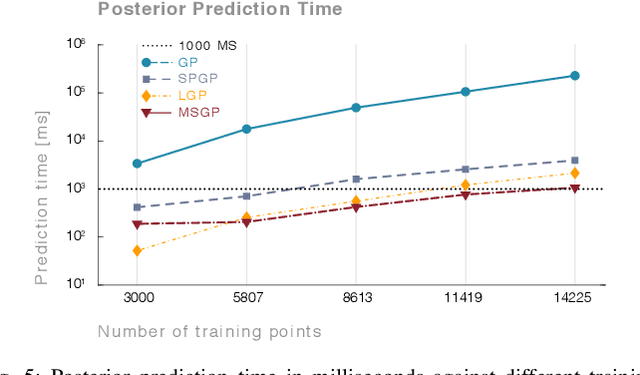
A key challenge with controlling complex dynamical systems is to accurately model them. However, this requirement is very hard to satisfy in practice. Data-driven approaches such as Gaussian processes (GPs) have proved quite effective by employing regression based methods to capture the unmodeled dynamical effects. However, GPs scale cubically with data, and is often a challenge to perform real-time regression. In this paper, we propose a semi-parametric framework exploiting sparsity for learning-based control. We combine the parametric model of the system with multiple sparse GP models to capture any unmodeled dynamics. Multi-Sparse Gaussian Process (MSGP) divides the original dataset into multiple sparse models with unique hyperparameters for each model. Thereby, preserving the richness and uniqueness of each sparse model. For a query point, a weighted sparse posterior prediction is performed based on $N$ neighboring sparse models. Hence, the prediction complexity is significantly reduced from $\mathcal{O}(n^3)$ to $\mathcal{O}(Npu^2)$, where $p$ and $u$ are data points and pseudo-inputs respectively for each sparse model. We validate MSGP's learning performance for a quadrotor using a geometric controller in simulation. Comparison with GP, sparse GP, and local GP shows that MSGP has higher prediction accuracy than sparse and local GP, while significantly lower time complexity than all three. We also validate MSGP on a hardware quadrotor for unmodeled mass, inertia, and disturbances. The experiment video can be seen at: https://youtu.be/zUk1ISux6ao

Online Parameter Estimation for Safety-Critical Systems with Gaussian Processes

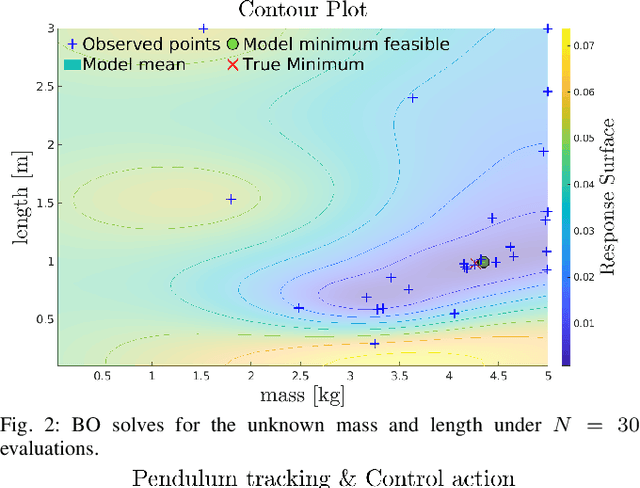
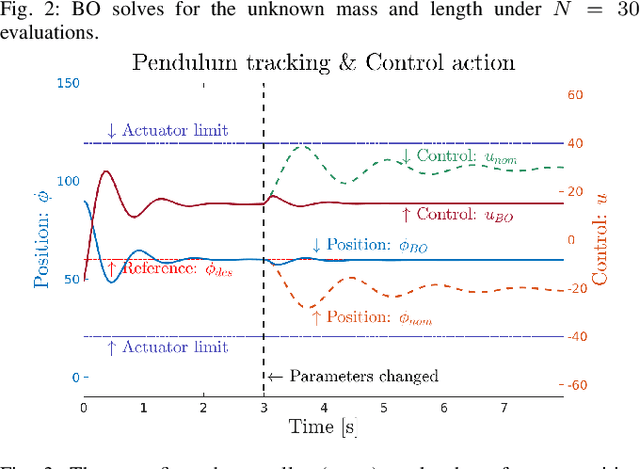
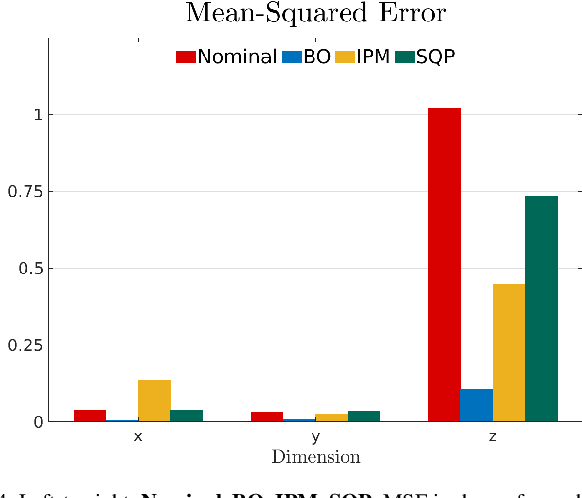
Parameter estimation is crucial for modeling, tracking, and control of complex dynamical systems. However, parameter uncertainties can compromise system performance under a controller relying on nominal parameter values. Typically, parameters are estimated using numerical regression approaches framed as inverse problems. However, they suffer from non-uniqueness due to existence of multiple local optima, reliance on gradients, numerous experimental data, or stability issues. Addressing these drawbacks, we present a Bayesian optimization framework based on Gaussian processes (GPs) for online parameter estimation. It uses an efficient search strategy over a response surface in the parameter space for finding the global optima with minimal function evaluations. The response surface is modeled as correlated surrogates using GPs on noisy data. The GP posterior predictive variance is exploited for smart adaptive sampling. This balances the exploration versus exploitation trade-off which is key in reaching the global optima under limited budget. We demonstrate our technique on an actuated planar pendulum and safety-critical quadrotor in simulation with changing parameters. We also benchmark our results against solvers using interior point method and sequential quadratic program. By reconfiguring the controller with new optimized parameters iteratively, we drastically improve trajectory tracking of the system versus the nominal case and other solvers.