Gaussian Control Barrier Functions : A Non-Parametric Paradigm to Safety

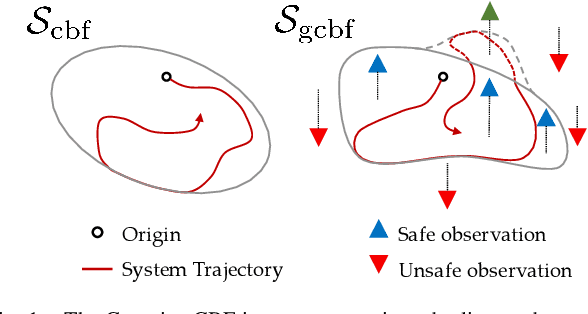
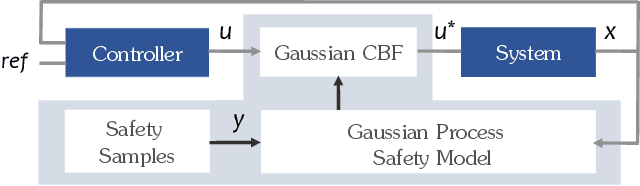
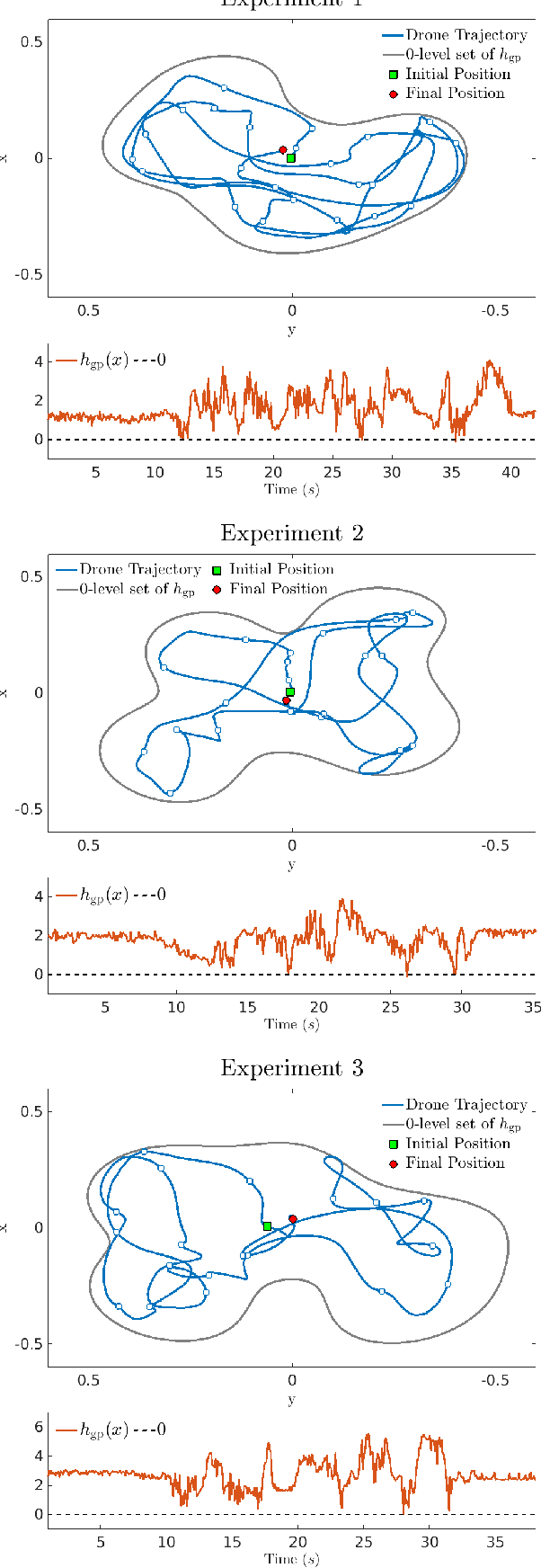
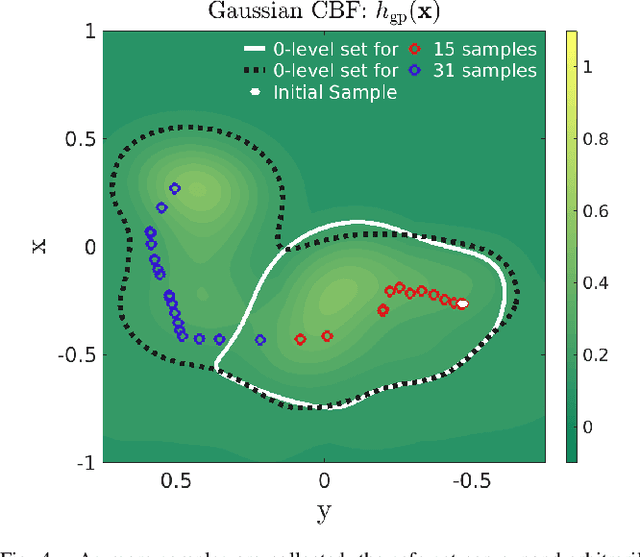
Inspired by the success of control barrier functions (CBFs) in addressing safety, and the rise of data-driven techniques for modeling functions, we propose a non-parametric approach for online synthesis of CBFs using Gaussian Processes (GPs). Mathematical constructs such as CBFs have achieved safety by designing a candidate function a priori. However, designing such a candidate function can be challenging. A practical example of such a setting would be to design a CBF in a disaster recovery scenario where safe and navigable regions need to be determined. The decision boundary for safety in such an example is unknown and cannot be designed a priori. In our approach, we work with safety samples or observations to construct the CBF online by assuming a flexible GP prior on these samples, and term our formulation as a Gaussian CBF. GPs have favorable properties, in addition to being non-parametric, such as analytical tractability and robust uncertainty estimation. This allows realizing the posterior components with high safety guarantees by incorporating variance estimation, while also computing associated partial derivatives in closed-form to achieve safe control. Moreover, the synthesized safety function from our approach allows changing the corresponding safe set arbitrarily based on the data, thus allowing non-convex safe sets. We validate our approach experimentally on a quadrotor by demonstrating safe control for fixed but arbitrary safe sets and collision avoidance where the safe set is constructed online. Finally, we juxtapose Gaussian CBFs with regular CBFs in the presence of noisy states to highlight its flexibility and robustness to noise. The experiment video can be seen at: https://youtu.be/HX6uokvCiGk

Multi-Sparse Gaussian Process: Learning based Semi-Parametric Control

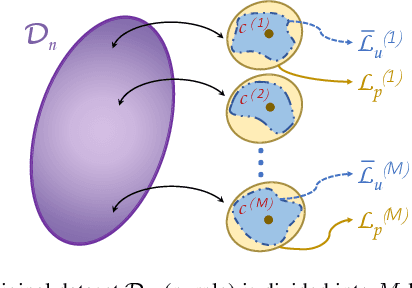
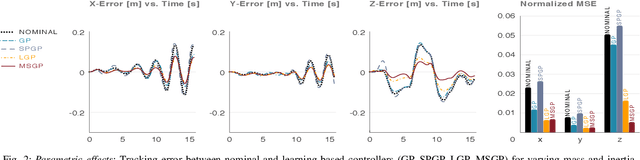
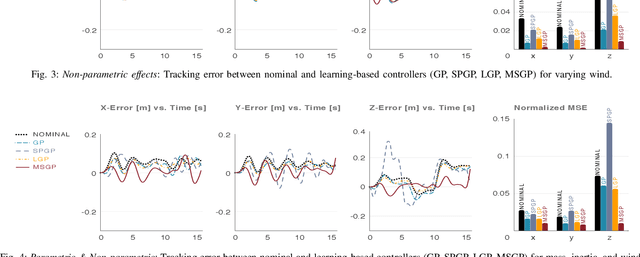
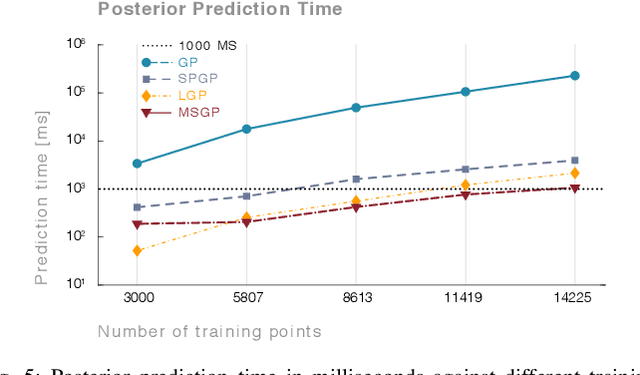
A key challenge with controlling complex dynamical systems is to accurately model them. However, this requirement is very hard to satisfy in practice. Data-driven approaches such as Gaussian processes (GPs) have proved quite effective by employing regression based methods to capture the unmodeled dynamical effects. However, GPs scale cubically with data, and is often a challenge to perform real-time regression. In this paper, we propose a semi-parametric framework exploiting sparsity for learning-based control. We combine the parametric model of the system with multiple sparse GP models to capture any unmodeled dynamics. Multi-Sparse Gaussian Process (MSGP) divides the original dataset into multiple sparse models with unique hyperparameters for each model. Thereby, preserving the richness and uniqueness of each sparse model. For a query point, a weighted sparse posterior prediction is performed based on $N$ neighboring sparse models. Hence, the prediction complexity is significantly reduced from $\mathcal{O}(n^3)$ to $\mathcal{O}(Npu^2)$, where $p$ and $u$ are data points and pseudo-inputs respectively for each sparse model. We validate MSGP's learning performance for a quadrotor using a geometric controller in simulation. Comparison with GP, sparse GP, and local GP shows that MSGP has higher prediction accuracy than sparse and local GP, while significantly lower time complexity than all three. We also validate MSGP on a hardware quadrotor for unmodeled mass, inertia, and disturbances. The experiment video can be seen at: https://youtu.be/zUk1ISux6ao

Online Parameter Estimation for Safety-Critical Systems with Gaussian Processes

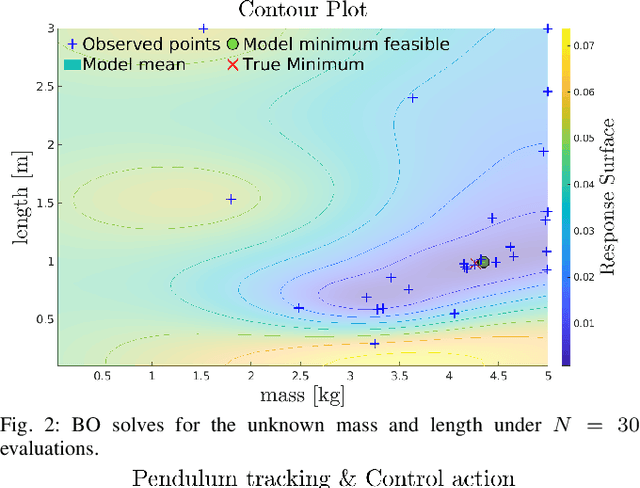
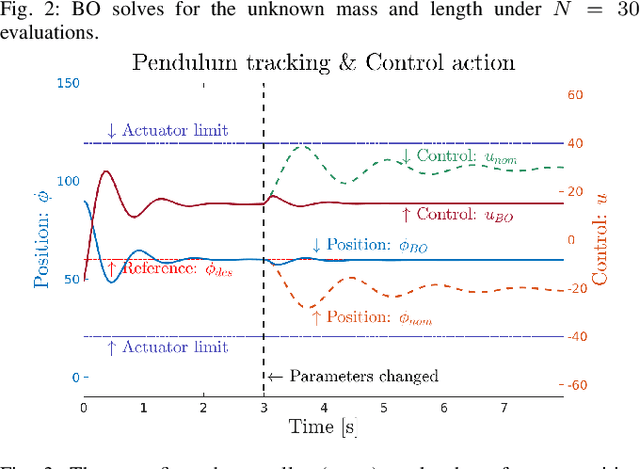
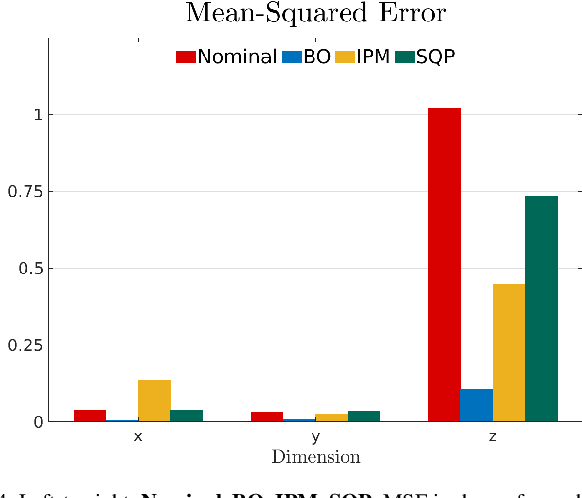
Parameter estimation is crucial for modeling, tracking, and control of complex dynamical systems. However, parameter uncertainties can compromise system performance under a controller relying on nominal parameter values. Typically, parameters are estimated using numerical regression approaches framed as inverse problems. However, they suffer from non-uniqueness due to existence of multiple local optima, reliance on gradients, numerous experimental data, or stability issues. Addressing these drawbacks, we present a Bayesian optimization framework based on Gaussian processes (GPs) for online parameter estimation. It uses an efficient search strategy over a response surface in the parameter space for finding the global optima with minimal function evaluations. The response surface is modeled as correlated surrogates using GPs on noisy data. The GP posterior predictive variance is exploited for smart adaptive sampling. This balances the exploration versus exploitation trade-off which is key in reaching the global optima under limited budget. We demonstrate our technique on an actuated planar pendulum and safety-critical quadrotor in simulation with changing parameters. We also benchmark our results against solvers using interior point method and sequential quadratic program. By reconfiguring the controller with new optimized parameters iteratively, we drastically improve trajectory tracking of the system versus the nominal case and other solvers.

On Realistic Target Coverage by Autonomous Drones

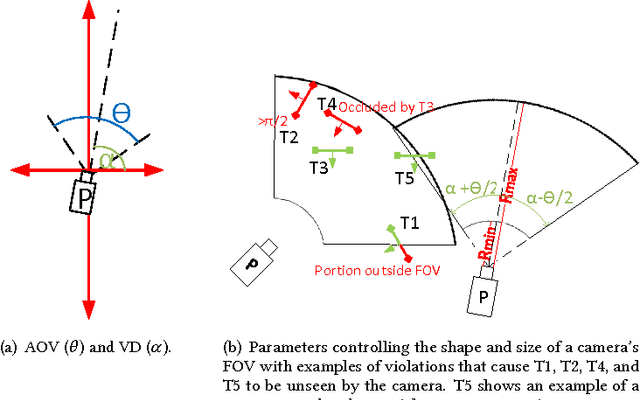
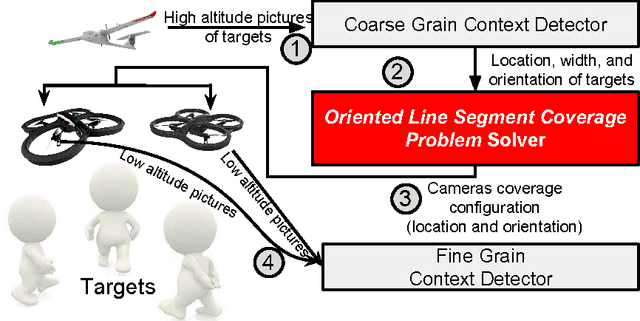
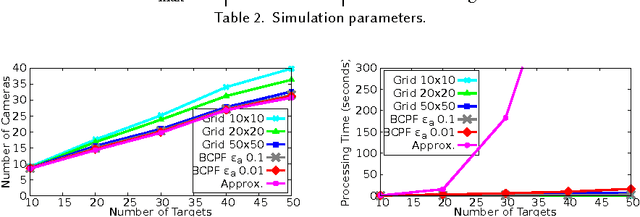
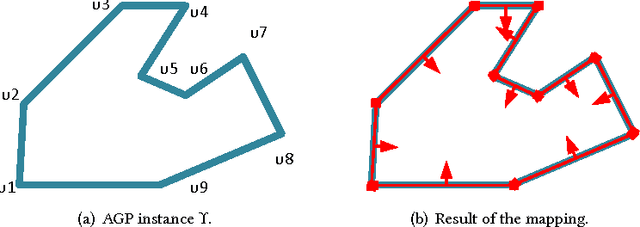
Low-cost mini-drones with advanced sensing and maneuverability enable a new class of intelligent sensing systems. To achieve the full potential of such drones, it is necessary to develop new enhanced formulations of both common and emerging sensing scenarios. Namely, several fundamental challenges in visual sensing remain unsolved including: 1) Fitting sizable targets in camera frames; 2) Effective viewpoints matching target poses; 3) Occlusion by elements in the environment, including other targets. In this paper, we introduce Argus: an autonomous system that utilizes drones to incrementally collect target information through a two-tier architecture. To tackle the stated challenges, Argus employs a novel geometric model that captures both target shapes and coverage constraints. Recognizing drones as the scarcest resource, Argus aims to minimize the number of drones required to cover a set of targets. We prove this problem is NP-hard, and even hard to approximate, before deriving a best-possible approximation algorithm along with a competitive sampling heuristic which runs up to 100x faster according to large-scale simulations. To test Argus in action, we demonstrate and analyze its performance on a prototype implementation. Finally, we present a number of extensions to accommodate more application requirements and highlight some open problems.