Multi-Sparse Gaussian Process: Learning based Semi-Parametric Control
Paper and Code
Mar 03, 2020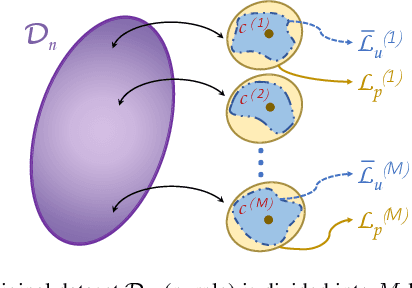
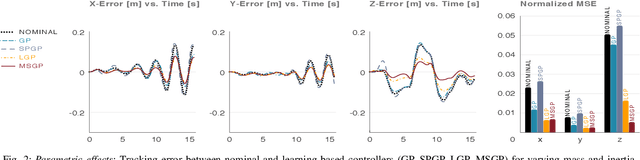
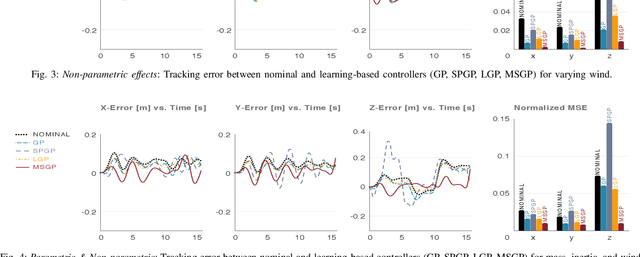
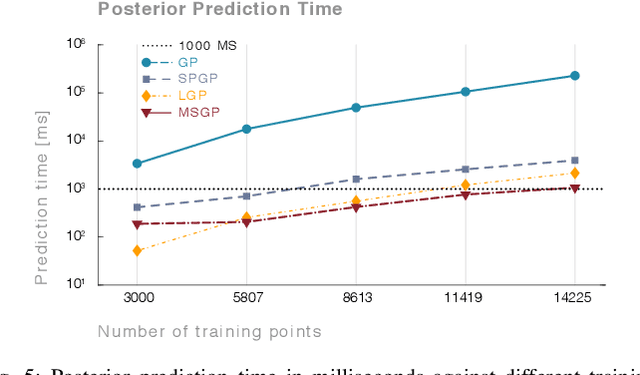
A key challenge with controlling complex dynamical systems is to accurately model them. However, this requirement is very hard to satisfy in practice. Data-driven approaches such as Gaussian processes (GPs) have proved quite effective by employing regression based methods to capture the unmodeled dynamical effects. However, GPs scale cubically with data, and is often a challenge to perform real-time regression. In this paper, we propose a semi-parametric framework exploiting sparsity for learning-based control. We combine the parametric model of the system with multiple sparse GP models to capture any unmodeled dynamics. Multi-Sparse Gaussian Process (MSGP) divides the original dataset into multiple sparse models with unique hyperparameters for each model. Thereby, preserving the richness and uniqueness of each sparse model. For a query point, a weighted sparse posterior prediction is performed based on $N$ neighboring sparse models. Hence, the prediction complexity is significantly reduced from $\mathcal{O}(n^3)$ to $\mathcal{O}(Npu^2)$, where $p$ and $u$ are data points and pseudo-inputs respectively for each sparse model. We validate MSGP's learning performance for a quadrotor using a geometric controller in simulation. Comparison with GP, sparse GP, and local GP shows that MSGP has higher prediction accuracy than sparse and local GP, while significantly lower time complexity than all three. We also validate MSGP on a hardware quadrotor for unmodeled mass, inertia, and disturbances. The experiment video can be seen at: https://youtu.be/zUk1ISux6ao
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge