Gaussian Belief Space Path Planning for Minimum Sensing Navigation
Paper and Code
Sep 28, 2021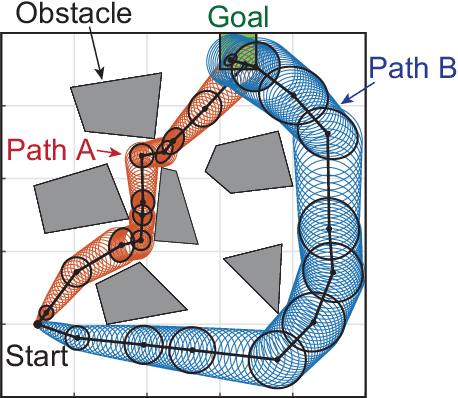

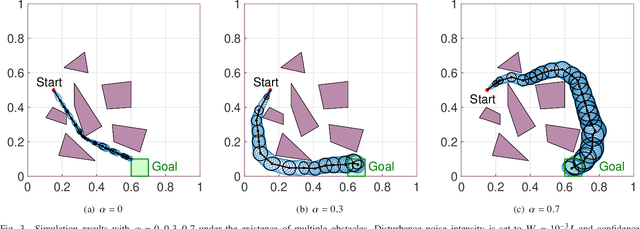
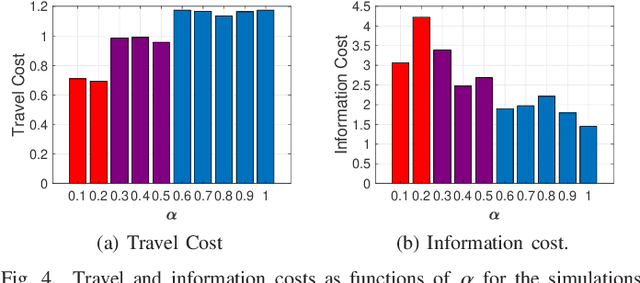
We propose a path planning methodology for a mobile robot navigating through an obstacle-filled environment to generate a reference path that is traceable with moderate sensing efforts. The desired reference path is characterized as the shortest path in an obstacle-filled Gaussian belief manifold equipped with a novel information-geometric distance function. The distance function we introduce is shown to be an asymmetric quasi-pseudometric and can be interpreted as the minimum information gain required to steer the Gaussian belief. An RRT*-based numerical solution algorithm is presented to solve the formulated shortest-path problem. To gain insight into the asymptotic optimality of the proposed algorithm, we show that the considered path length function is continuous with respect to the topology of total variation. Simulation results demonstrate that the proposed method is effective in various robot navigation scenarios to reduce sensing costs, such as the required frequency of sensor measurements and the number of sensors that must be operated simultaneously.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge