Dynamic Allocation of Visual Attention for Vision-based Autonomous Navigation under Data Rate Constraints
Paper and Code
Sep 27, 2021

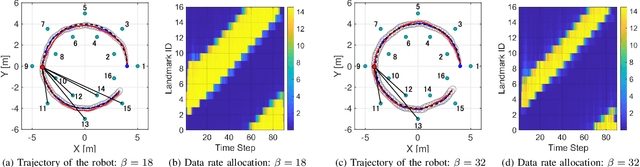
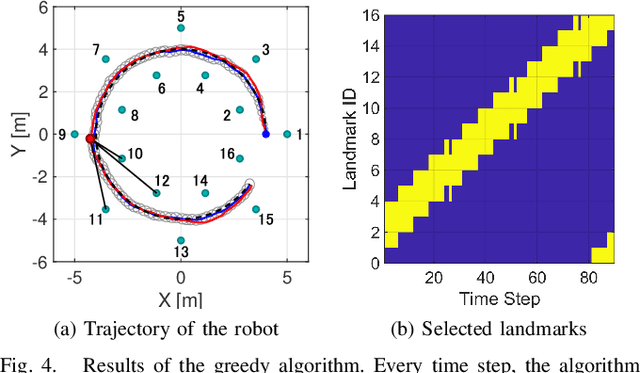
This paper considers the problem of task-dependent (top-down) attention allocation for vision-based autonomous navigation using known landmarks. Unlike the existing paradigm in which landmark selection is formulated as a combinatorial optimization problem, we model it as a resource allocation problem where the decision-maker (DM) is granted extra freedom to control the degree of attention to each landmark. The total resource available to DM is expressed in terms of the capacity limit of the in-take information flow, which is quantified by the directed information from the state of the environment to the DM's observation. We consider a receding horizon implementation of such a controlled sensing scheme in the Linear-Quadratic-Gaussian (LQG) regime. The convex-concave procedure is applied in each time step, whose time complexity is shown to be linear in the horizon length if the alternating direction method of multipliers (ADMM) is used. Numerical studies show that the proposed formulation is sparsity-promoting in the sense that it tends to allocate zero data rate to uninformative landmarks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge