Surrogate Model-Based Near-Optimal Gain Selection for Approach-Angle-Constrained Two-Phase Pure Proportional Navigation

In guidance literature, Pure Proportional Navigation (PPN) guidance is widely used for aerodynamically driven vehicles. A two-phase extension of PPN (2pPPN), which uses different navigation gains for an orientation phase and a final phase, has been presented to achieve any desired approach angle within an angular half-space. Recent studies show that the orientation phase can be realized through multiple feasible trajectories, creating an opportunity to select navigation gains that minimize overall guidance effort. This paper addresses the problem of near-optimal gain selection for given initial and desired terminal engagement geometries. Two optimization problems are considered: i) determination of the optimal orientation-phase gain for a specified final-phase gain, and ii) simultaneously determining the optimal gain pair for both phases that minimizes the total guidance effort. Determining the optimal gains analytically for arbitrary engagement geometries is intractable. Numerical simulations further reveal that these optimal gains vary smoothly with respect to the engagement conditions. Exploiting this property, a neural network (NN)-based regression model is developed in this paper to learn the nonlinear mapping between optimal gains and initial and desired terminal engagement geometries. The trained NN serves as a computationally efficient surrogate for generating the optimal gains manifold, enabling near-optimal realization of 2pPPN guidance. Numerical simulation studies demonstrate that the developed NN-based architecture predicts optimal gains with high accuracy, achieving very high (close to 0.9) value of coefficient of determination.

A Corrector-aided Look-ahead Distance-based Guidance for Reference Path Following with an Efficient Midcourse Guidance Strategy

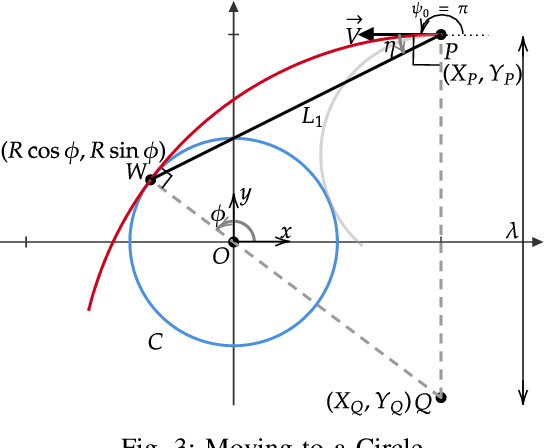
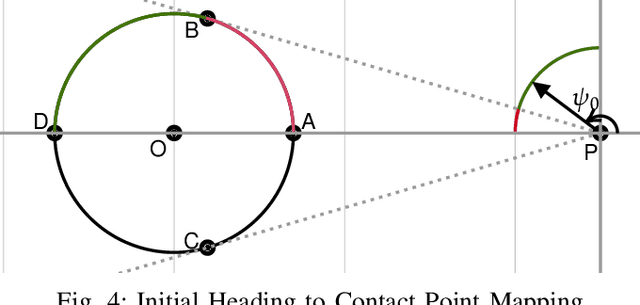
Efficient path-following is crucial in most of the applications of autonomous vehicles (UxV). Among various guidance strategies presented in literature, look-ahead distance ($L_1$)-based guidance method has received significant attention due to its ease in implementation and ability to maintain a low cross-track error while following simpler reference paths and generate bounded lateral acceleration commands. However, the constant value of $L_1$ becomes problematic when the UxV is far away from the reference path and also produce higher cross-track error while following complex reference paths having high variation in radius of curvature. To address these challenges, the notion of look-ahead distance is leveraged in a novel way to develop a two-phase guidance strategy. Initially, when the UxV is far from the reference path, an optimized $L_1$ selection strategy is developed to guide the UxV toward the reference path in order to maintain minimal lateral acceleration command. Once the vehicle reaches a close vicinity of the reference path, a novel notion of corrector point is incorporated in the constant $L_1$-based guidance scheme to generate the lateral acceleration command that effectively reduces the root mean square of the cross-track error thereafter. Simulation results demonstrate that this proposed corrector point and look-ahead point pair-based guidance strategy along with the developed midcourse guidance scheme outperforms the conventional constant $L_1$ guidance scheme both in terms of feasibility and measures of effectiveness like cross-track error and lateral acceleration requirements.

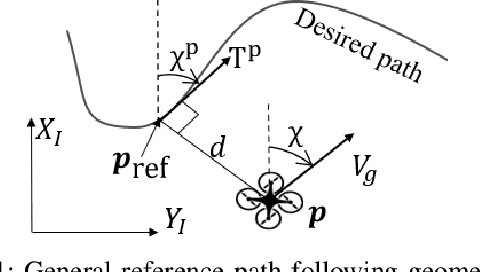
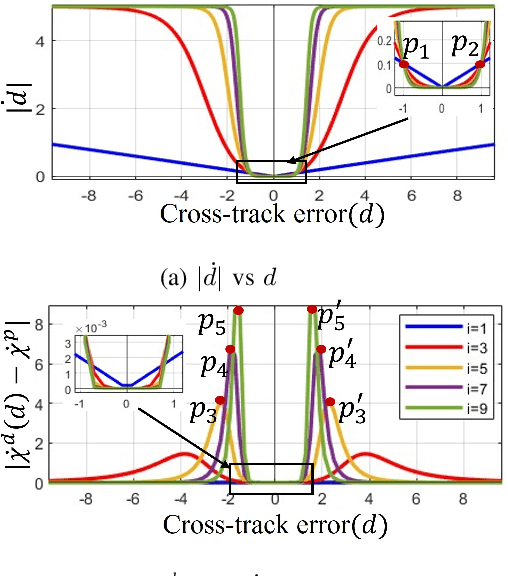
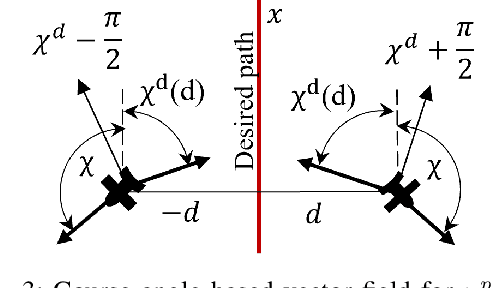
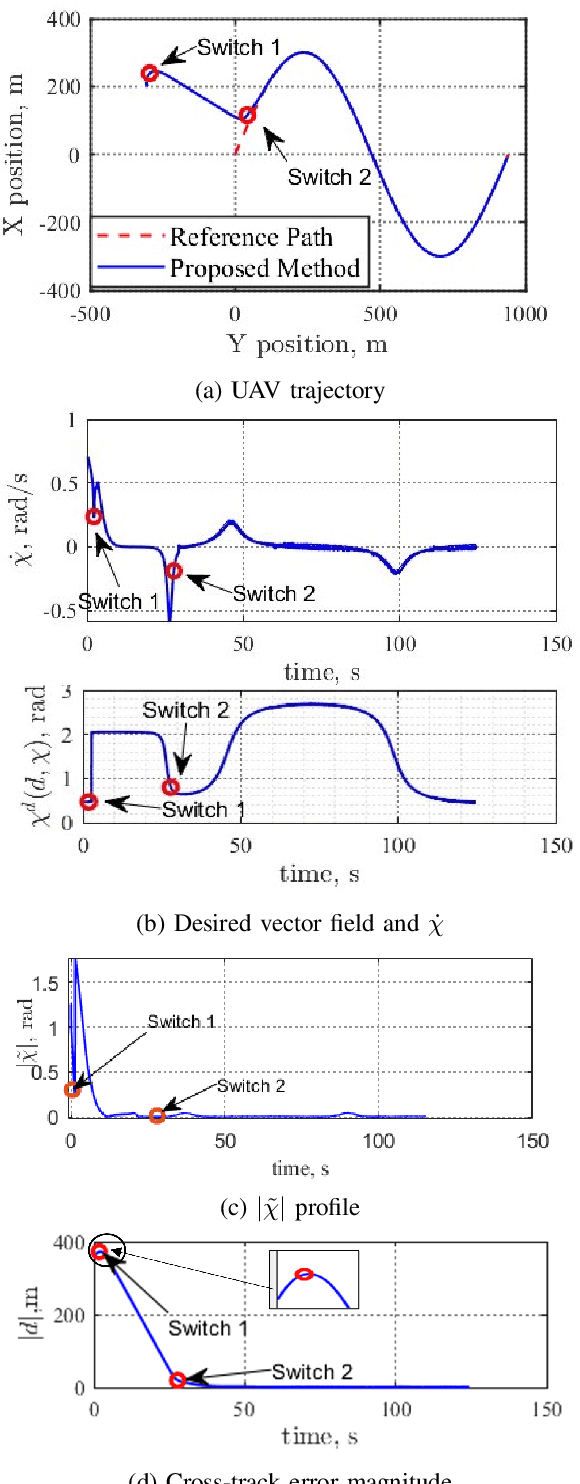
Switched Vector Field-based Guidance for General Reference Path Following in Planar Environment

Reference path following is a key component in the functioning of almost all engineered autonomous agents. Among several path following guidance methods in existing literature, vector-field-based guidance approach has got wide attention because of its simplicity and guarantee of stability under a broad class of scenarios. However, the usage of same cross-track-error-dependent structure of desired vector field in most of the existing literature irrespective of instantaneous cross-track error and course angle of unmanned vehicle makes it quite restrictive in attaining faster convergence and also leads to infeasibly high turn rate command for many scenarios. To this end, this paper presents a novel switched vector field-based guidance for following a general reference path, in which the structure of the desired vector field depends on instantaneous cross-track-error and vehicle's course angle. While the developed method ensures faster convergence, it also ensures that the guidance command always stays within a realistic threshold satisfying its curvature constraint, thus making it more real-life implementable for autonomous vehicles with kino-dynamic constraints. Theoretical analysis for convergence of the developed guidance scheme is presented. Possibilities of undesirable chattering at phase transitions are also eliminated. Numerical simulation studies are presented to validate the satisfactory performance of the developed algorithm.

Fuel-Optimal Powered Descent Guidance for Hazardous Terrain

Future interplanetary missions will carry more and more sensitive equipment critical for setting up bases for crewed missions. The ability to manoeuvre around hazardous terrain thus becomes a critical mission aspect. However, large diverts and manoeuvres consume a significant amount of fuel, leading to less fuel remaining for emergencies or return missions. Thus, requiring more fuel to be carried onboard. This work presents fuel-optimal guidance to avoid hazardous terrain and safely land at the desired location. We approximate the hazardous terrain as step-shaped polygons and define barriers around the terrain. Using an augmented cost functional, fuel-optimal guidance command, which avoids the terrain, is derived. The results are validated using computer simulations and tested against many initial conditions to prove their effectiveness.

Mathematical Properties of Generalized Shape Expansion-Based Motion Planning Algorithms

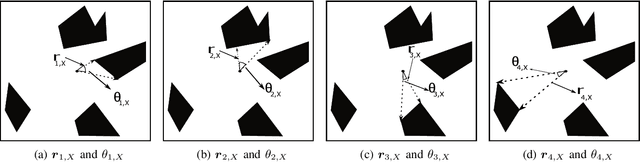
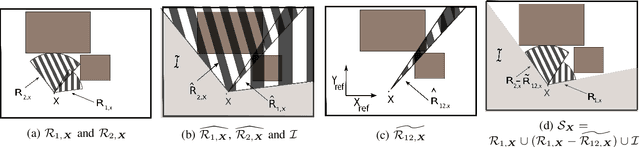
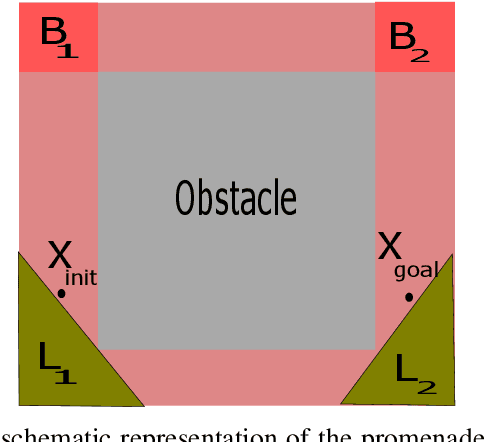
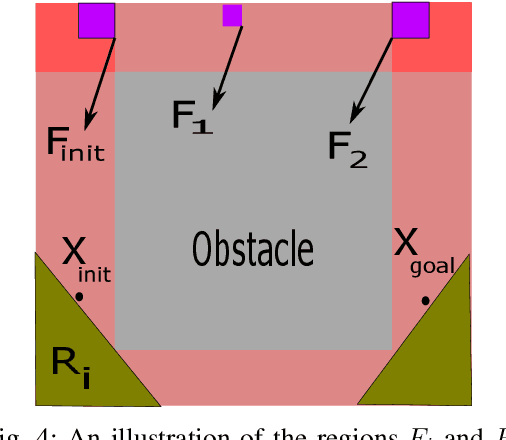
Motion planning is an essential aspect of autonomous systems and robotics and is an active area of research. A recently-proposed sampling-based motion planning algorithm, termed 'Generalized Shape Expansion' (GSE), has been shown to possess significant improvement in computational time over several existing well-established algorithms. The GSE has also been shown to be probabilistically complete. However, asymptotic optimality of the GSE is yet to be studied. To this end, in this paper we show that the GSE algorithm is not asymptotically optimal by studying its behaviour for the promenade problem. In order to obtain a probabilistically complete and asymptotically optimal generalized shape-based algorithm, a modified version of the GSE, namely 'GSE*' algorithm, is subsequently presented. The forementioned desired mathematical properties of the GSE* algorithm are justified by its detailed analysis. Numerical simulations are found to be in line with the theoretical results on the GSE* algorithm.