Path Integral Control with Rollout Clustering and Dynamic Obstacles

Model Predictive Path Integral (MPPI) control has proven to be a powerful tool for the control of uncertain systems (such as systems subject to disturbances and systems with unmodeled dynamics). One important limitation of the baseline MPPI algorithm is that it does not utilize simulated trajectories to their fullest extent. For one, it assumes that the average of all trajectories weighted by their performance index will be a safe trajectory. In this paper, multiple examples are shown where the previous assumption does not hold, and a trajectory clustering technique is presented that reduces the chances of the weighted average crossing in an unsafe region. Secondly, MPPI does not account for dynamic obstacles, so the authors put forward a novel cost function that accounts for dynamic obstacles without adding significant computation time to the overall algorithm. The novel contributions proposed in this paper were evaluated with extensive simulations to demonstrate improvements upon the state-of-the-art MPPI techniques.

Collision Avoidance Using Spherical Harmonics

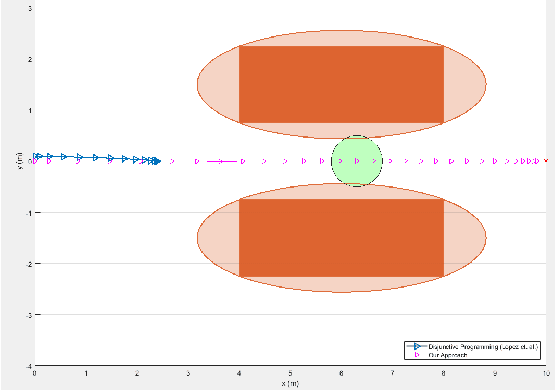
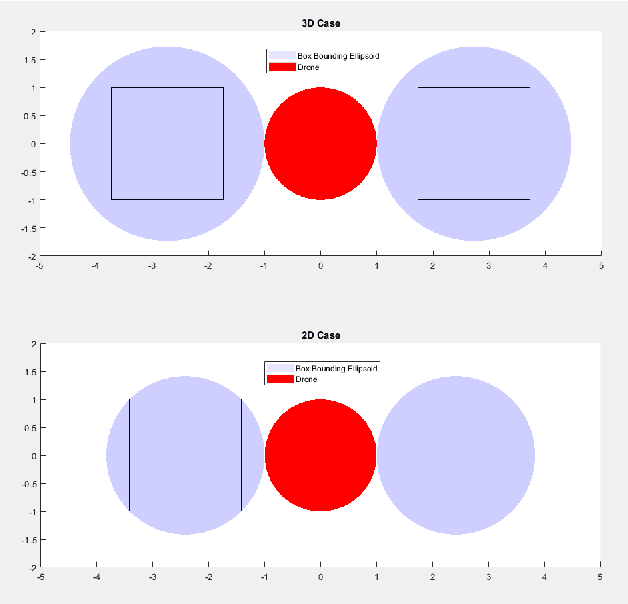
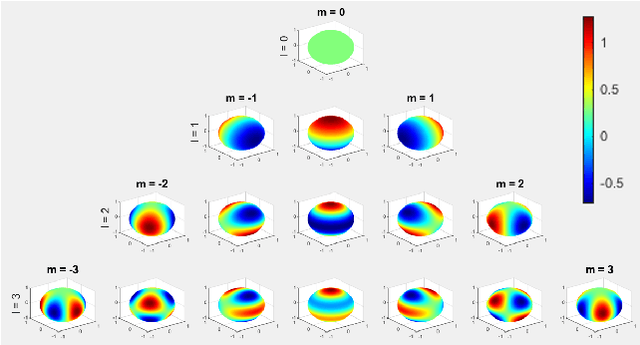
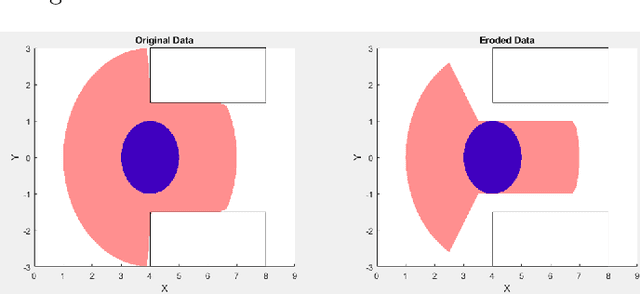
In this paper, we propose a novel optimization-based trajectory planner that utilizes spherical harmonics to estimate the collision-free solution space around an agent. The space is estimated using a constrained over-determined least-squares estimator to determine the parameters that define a spherical harmonic approximation at a given time step. Since spherical harmonics produce star-convex shapes, the planner can consider all paths that are in line-of-sight for the agent within a given radius. This contrasts with other state-of-the-art planners that generate trajectories by estimating obstacle boundaries with rough approximations and using heuristic rules to prune a solution space into one that can be easily explored. Those methods cause the trajectory planner to be overly conservative in environments where an agent must get close to obstacles to accomplish a goal. Our method is shown to perform on-par with other path planners and surpass these planners in certain environments. It generates feasible trajectories while still running in real-time and guaranteeing safety when a valid solution exists.