Discrete Adjoint Schrödinger Bridge Sampler

Learning discrete neural samplers is challenging due to the lack of gradients and combinatorial complexity. While stochastic optimal control (SOC) and Schrödinger bridge (SB) provide principled solutions, efficient SOC solvers like adjoint matching (AM), which excel in continuous domains, remain unexplored for discrete spaces. We bridge this gap by revealing that the core mechanism of AM is $\mathit{state}\text{-}\mathit{space~agnostic}$, and introduce $\mathbf{discrete~ASBS}$, a unified framework that extends AM and adjoint Schrödinger bridge sampler (ASBS) to discrete spaces. Theoretically, we analyze the optimality conditions of the discrete SB problem and its connection to SOC, identifying a necessary cyclic group structure on the state space to enable this extension. Empirically, discrete ASBS achieves competitive sample quality with significant advantages in training efficiency and scalability.

Discrete Adjoint Matching

Computation methods for solving entropy-regularized reward optimization -- a class of problems widely used for fine-tuning generative models -- have advanced rapidly. Among those, Adjoint Matching (AM, Domingo-Enrich et al., 2025) has proven highly effective in continuous state spaces with differentiable rewards. Transferring these practical successes to discrete generative modeling, however, remains particularly challenging and largely unexplored, mainly due to the drastic shift in generative model classes to discrete state spaces, which are nowhere differentiable. In this work, we propose Discrete Adjoint Matching (DAM) -- a discrete variant of AM for fine-tuning discrete generative models characterized by Continuous-Time Markov Chains, such as diffusion-based large language models. The core of DAM is the introduction of discrete adjoint-an estimator of the optimal solution to the original problem but formulated on discrete domains-from which standard matching frameworks can be applied. This is derived via a purely statistical standpoint, in contrast to the control-theoretic viewpoint in AM, thereby opening up new algorithmic opportunities for general adjoint-based estimators. We showcase DAM's effectiveness on synthetic and mathematical reasoning tasks.

Functional Adjoint Sampler: Scalable Sampling on Infinite Dimensional Spaces

Learning-based methods for sampling from the Gibbs distribution in finite-dimensional spaces have progressed quickly, yet theory and algorithmic design for infinite-dimensional function spaces remain limited. This gap persists despite their strong potential for sampling the paths of conditional diffusion processes, enabling efficient simulation of trajectories of diffusion processes that respect rare events or boundary constraints. In this work, we present the adjoint sampler for infinite-dimensional function spaces, a stochastic optimal control-based diffusion sampler that operates in function space and targets Gibbs-type distributions on infinite-dimensional Hilbert spaces. Our Functional Adjoint Sampler (FAS) generalizes Adjoint Sampling (Havens et al., 2025) to Hilbert spaces based on a SOC theory called stochastic maximum principle, yielding a simple and scalable matching-type objective for a functional representation. We show that FAS achieves superior transition path sampling performance across synthetic potential and real molecular systems, including Alanine Dipeptide and Chignolin.

Optimal Control Theoretic Neural Optimizer: From Backpropagation to Dynamic Programming

Optimization of deep neural networks (DNNs) has been a driving force in the advancement of modern machine learning and artificial intelligence. With DNNs characterized by a prolonged sequence of nonlinear propagation, determining their optimal parameters given an objective naturally fits within the framework of Optimal Control Programming. Such an interpretation of DNNs as dynamical systems has proven crucial in offering a theoretical foundation for principled analysis from numerical equations to physics. In parallel to these theoretical pursuits, this paper focuses on an algorithmic perspective. Our motivated observation is the striking algorithmic resemblance between the Backpropagation algorithm for computing gradients in DNNs and the optimality conditions for dynamical systems, expressed through another backward process known as dynamic programming. Consolidating this connection, where Backpropagation admits a variational structure, solving an approximate dynamic programming up to the first-order expansion leads to a new class of optimization methods exploring higher-order expansions of the Bellman equation. The resulting optimizer, termed Optimal Control Theoretic Neural Optimizer (OCNOpt), enables rich algorithmic opportunities, including layer-wise feedback policies, game-theoretic applications, and higher-order training of continuous-time models such as Neural ODEs. Extensive experiments demonstrate that OCNOpt improves upon existing methods in robustness and efficiency while maintaining manageable computational complexity, paving new avenues for principled algorithmic design grounded in dynamical systems and optimal control theory.

Momentum Multi-Marginal Schrödinger Bridge Matching

Understanding complex systems by inferring trajectories from sparse sample snapshots is a fundamental challenge in a wide range of domains, e.g., single-cell biology, meteorology, and economics. Despite advancements in Bridge and Flow matching frameworks, current methodologies rely on pairwise interpolation between adjacent snapshots. This hinders their ability to capture long-range temporal dependencies and potentially affects the coherence of the inferred trajectories. To address these issues, we introduce \textbf{Momentum Multi-Marginal Schr\"odinger Bridge Matching (3MSBM)}, a novel matching framework that learns smooth measure-valued splines for stochastic systems that satisfy multiple positional constraints. This is achieved by lifting the dynamics to phase space and generalizing stochastic bridges to be conditioned on several points, forming a multi-marginal conditional stochastic optimal control problem. The underlying dynamics are then learned by minimizing a variational objective, having fixed the path induced by the multi-marginal conditional bridge. As a matching approach, 3MSBM learns transport maps that preserve intermediate marginals throughout training, significantly improving convergence and scalability. Extensive experimentation in a series of real-world applications validates the superior performance of 3MSBM compared to existing methods in capturing complex dynamics with temporal dependencies, opening new avenues for training matching frameworks in multi-marginal settings.

Adjoint Sampling: Highly Scalable Diffusion Samplers via Adjoint Matching

We introduce Adjoint Sampling, a highly scalable and efficient algorithm for learning diffusion processes that sample from unnormalized densities, or energy functions. It is the first on-policy approach that allows significantly more gradient updates than the number of energy evaluations and model samples, allowing us to scale to much larger problem settings than previously explored by similar methods. Our framework is theoretically grounded in stochastic optimal control and shares the same theoretical guarantees as Adjoint Matching, being able to train without the need for corrective measures that push samples towards the target distribution. We show how to incorporate key symmetries, as well as periodic boundary conditions, for modeling molecules in both cartesian and torsional coordinates. We demonstrate the effectiveness of our approach through extensive experiments on classical energy functions, and further scale up to neural network-based energy models where we perform amortized conformer generation across many molecular systems. To encourage further research in developing highly scalable sampling methods, we plan to open source these challenging benchmarks, where successful methods can directly impact progress in computational chemistry.

Deep Generalized Schrödinger Bridges: From Image Generation to Solving Mean-Field Games

Generalized Schr\"odinger Bridges (GSBs) are a fundamental mathematical framework used to analyze the most likely particle evolution based on the principle of least action including kinetic and potential energy. In parallel to their well-established presence in the theoretical realms of quantum mechanics and optimal transport, this paper focuses on an algorithmic perspective, aiming to enhance practical usage. Our motivated observation is that transportation problems with the optimality structures delineated by GSBs are pervasive across various scientific domains, such as generative modeling in machine learning, mean-field games in stochastic control, and more. Exploring the intrinsic connection between the mathematical modeling of GSBs and the modern algorithmic characterization therefore presents a crucial, yet untapped, avenue. In this paper, we reinterpret GSBs as probabilistic models and demonstrate that, with a delicate mathematical tool known as the nonlinear Feynman-Kac lemma, rich algorithmic concepts, such as likelihoods, variational gaps, and temporal differences, emerge naturally from the optimality structures of GSBs. The resulting computational framework, driven by deep learning and neural networks, operates in a fully continuous state space (i.e., mesh-free) and satisfies distribution constraints, setting it apart from prior numerical solvers relying on spatial discretization or constraint relaxation. We demonstrate the efficacy of our method in generative modeling and mean-field games, highlighting its transformative applications at the intersection of mathematical modeling, stochastic process, control, and machine learning.

Feedback Schrödinger Bridge Matching

Recent advancements in diffusion bridges for distribution transport problems have heavily relied on matching frameworks, yet existing methods often face a trade-off between scalability and access to optimal pairings during training. Fully unsupervised methods make minimal assumptions but incur high computational costs, limiting their practicality. On the other hand, imposing full supervision of the matching process with optimal pairings improves scalability, however, it can be infeasible in many applications. To strike a balance between scalability and minimal supervision, we introduce Feedback Schr\"odinger Bridge Matching (FSBM), a novel semi-supervised matching framework that incorporates a small portion (less than 8% of the entire dataset) of pre-aligned pairs as state feedback to guide the transport map of non coupled samples, thereby significantly improving efficiency. This is achieved by formulating a static Entropic Optimal Transport (EOT) problem with an additional term capturing the semi-supervised guidance. The generalized EOT objective is then recast into a dynamic formulation to leverage the scalability of matching frameworks. Extensive experiments demonstrate that FSBM accelerates training and enhances generalization by leveraging coupled pairs guidance, opening new avenues for training matching frameworks with partially aligned datasets.

React-OT: Optimal Transport for Generating Transition State in Chemical Reactions

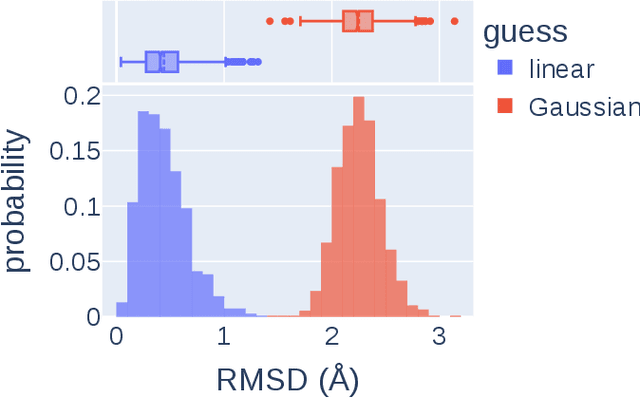
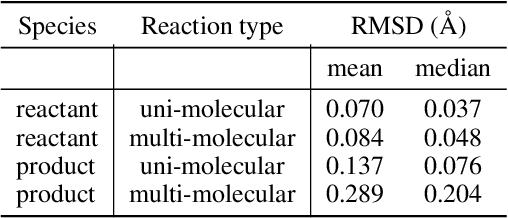
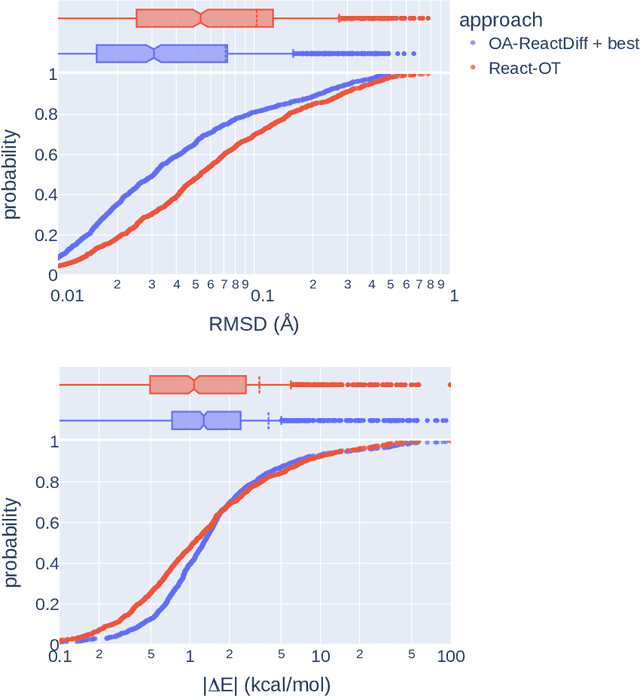
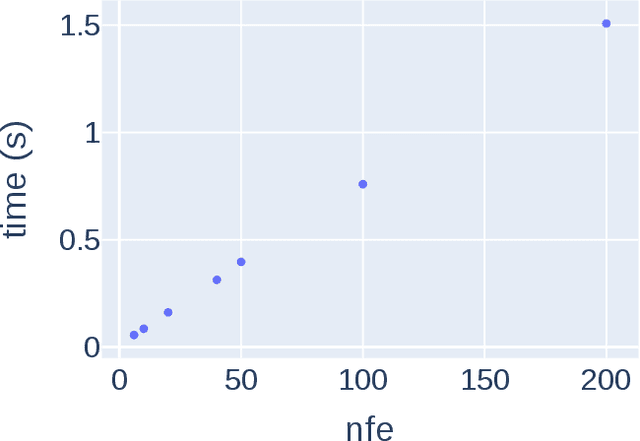
Transition states (TSs) are transient structures that are key in understanding reaction mechanisms and designing catalysts but challenging to be captured in experiments. Alternatively, many optimization algorithms have been developed to search for TSs computationally. Yet the cost of these algorithms driven by quantum chemistry methods (usually density functional theory) is still high, posing challenges for their applications in building large reaction networks for reaction exploration. Here we developed React-OT, an optimal transport approach for generating unique TS structures from reactants and products. React-OT generates highly accurate TS structures with a median structural root mean square deviation (RMSD) of 0.053{\AA} and median barrier height error of 1.06 kcal/mol requiring only 0.4 second per reaction. The RMSD and barrier height error is further improved by roughly 25% through pretraining React-OT on a large reaction dataset obtained with a lower level of theory, GFN2-xTB. We envision the great accuracy and fast inference of React-OT useful in targeting TSs when exploring chemical reactions with unknown mechanisms.

Augmented Bridge Matching

Flow and bridge matching are a novel class of processes which encompass diffusion models. One of the main aspect of their increased flexibility is that these models can interpolate between arbitrary data distributions i.e. they generalize beyond generative modeling and can be applied to learning stochastic (and deterministic) processes of arbitrary transfer tasks between two given distributions. In this paper, we highlight that while flow and bridge matching processes preserve the information of the marginal distributions, they do \emph{not} necessarily preserve the coupling information unless additional, stronger optimality conditions are met. This can be problematic if one aims at preserving the original empirical pairing. We show that a simple modification of the matching process recovers this coupling by augmenting the velocity field (or drift) with the information of the initial sample point. Doing so, we lose the Markovian property of the process but preserve the coupling information between distributions. We illustrate the efficiency of our augmentation in learning mixture of image translation tasks.