Capabilities of Large Language Models in Control Engineering: A Benchmark Study on GPT-4, Claude 3 Opus, and Gemini 1.0 Ultra

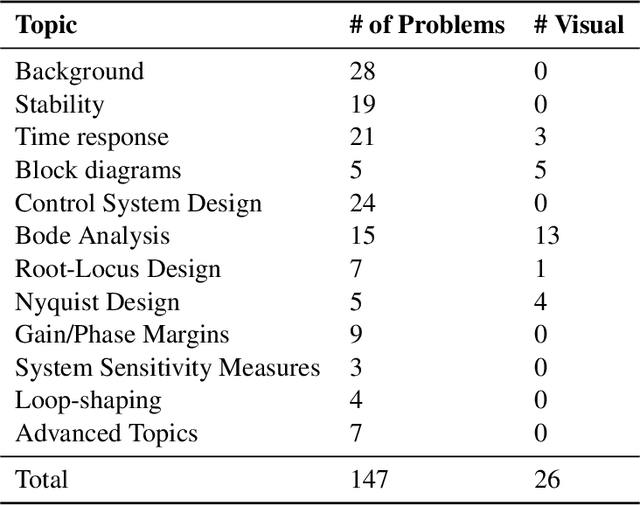
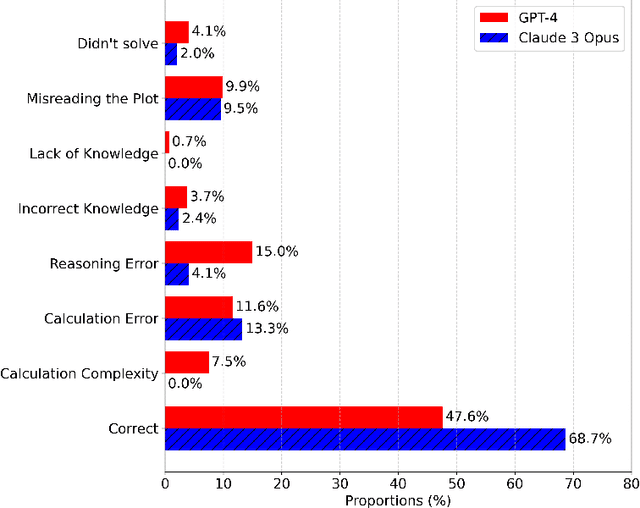
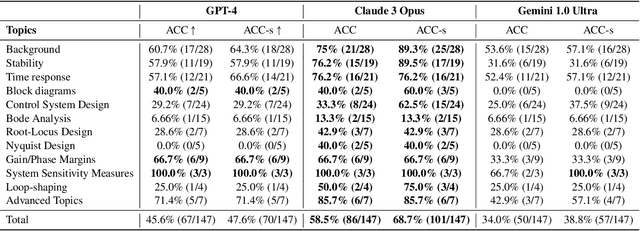
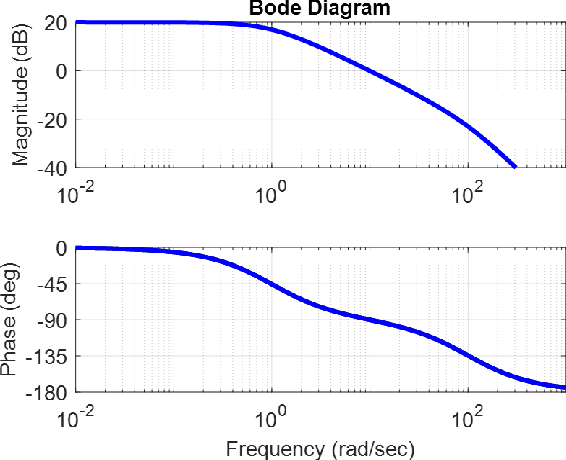
In this paper, we explore the capabilities of state-of-the-art large language models (LLMs) such as GPT-4, Claude 3 Opus, and Gemini 1.0 Ultra in solving undergraduate-level control problems. Controls provides an interesting case study for LLM reasoning due to its combination of mathematical theory and engineering design. We introduce ControlBench, a benchmark dataset tailored to reflect the breadth, depth, and complexity of classical control design. We use this dataset to study and evaluate the problem-solving abilities of these LLMs in the context of control engineering. We present evaluations conducted by a panel of human experts, providing insights into the accuracy, reasoning, and explanatory prowess of LLMs in control engineering. Our analysis reveals the strengths and limitations of each LLM in the context of classical control, and our results imply that Claude 3 Opus has become the state-of-the-art LLM for solving undergraduate control problems. Our study serves as an initial step towards the broader goal of employing artificial general intelligence in control engineering.

Novel Quadratic Constraints for Extending LipSDP beyond Slope-Restricted Activations

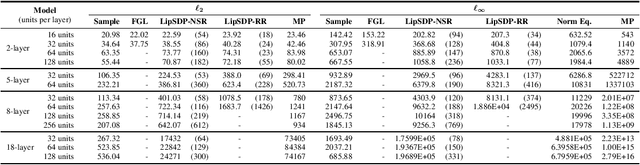
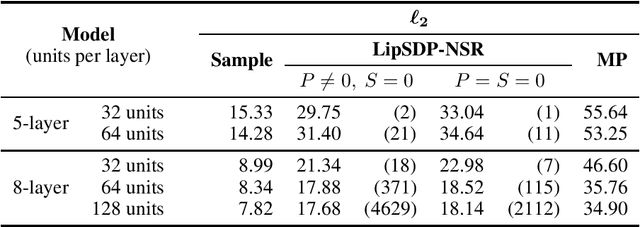
Recently, semidefinite programming (SDP) techniques have shown great promise in providing accurate Lipschitz bounds for neural networks. Specifically, the LipSDP approach (Fazlyab et al., 2019) has received much attention and provides the least conservative Lipschitz upper bounds that can be computed with polynomial time guarantees. However, one main restriction of LipSDP is that its formulation requires the activation functions to be slope-restricted on $[0,1]$, preventing its further use for more general activation functions such as GroupSort, MaxMin, and Householder. One can rewrite MaxMin activations for example as residual ReLU networks. However, a direct application of LipSDP to the resultant residual ReLU networks is conservative and even fails in recovering the well-known fact that the MaxMin activation is 1-Lipschitz. Our paper bridges this gap and extends LipSDP beyond slope-restricted activation functions. To this end, we provide novel quadratic constraints for GroupSort, MaxMin, and Householder activations via leveraging their underlying properties such as sum preservation. Our proposed analysis is general and provides a unified approach for estimating $\ell_2$ and $\ell_\infty$ Lipschitz bounds for a rich class of neural network architectures, including non-residual and residual neural networks and implicit models, with GroupSort, MaxMin, and Householder activations. Finally, we illustrate the utility of our approach with a variety of experiments and show that our proposed SDPs generate less conservative Lipschitz bounds in comparison to existing approaches.

A Unified Algebraic Perspective on Lipschitz Neural Networks

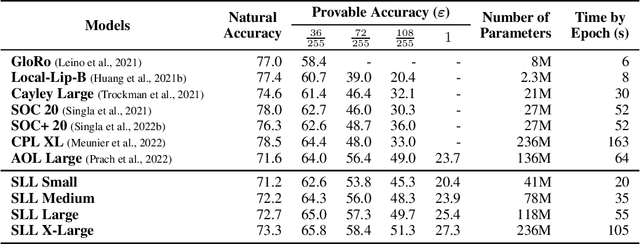
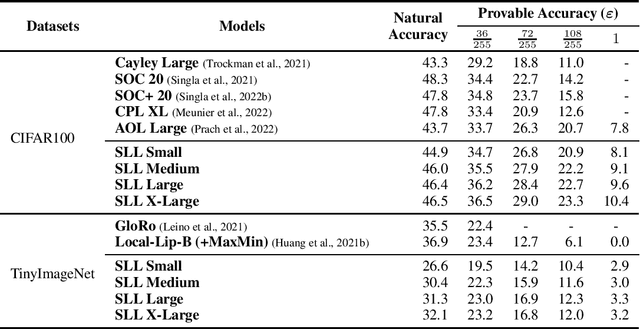
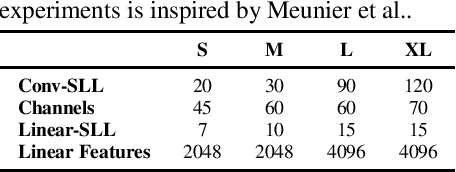
Important research efforts have focused on the design and training of neural networks with a controlled Lipschitz constant. The goal is to increase and sometimes guarantee the robustness against adversarial attacks. Recent promising techniques draw inspirations from different backgrounds to design 1-Lipschitz neural networks, just to name a few: convex potential layers derive from the discretization of continuous dynamical systems, Almost-Orthogonal-Layer proposes a tailored method for matrix rescaling. However, it is today important to consider the recent and promising contributions in the field under a common theoretical lens to better design new and improved layers. This paper introduces a novel algebraic perspective unifying various types of 1-Lipschitz neural networks, including the ones previously mentioned, along with methods based on orthogonality and spectral methods. Interestingly, we show that many existing techniques can be derived and generalized via finding analytical solutions of a common semidefinite programming (SDP) condition. We also prove that AOL biases the scaled weight to the ones which are close to the set of orthogonal matrices in a certain mathematical manner. Moreover, our algebraic condition, combined with the Gershgorin circle theorem, readily leads to new and diverse parameterizations for 1-Lipschitz network layers. Our approach, called SDP-based Lipschitz Layers (SLL), allows us to design non-trivial yet efficient generalization of convex potential layers. Finally, the comprehensive set of experiments on image classification shows that SLLs outperform previous approaches on certified robust accuracy. Code is available at https://github.com/araujoalexandre/Lipschitz-SLL-Networks.

Revisiting PGD Attacks for Stability Analysis of Large-Scale Nonlinear Systems and Perception-Based Control

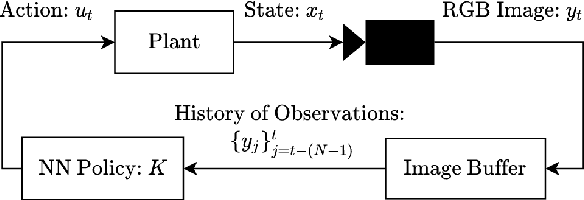
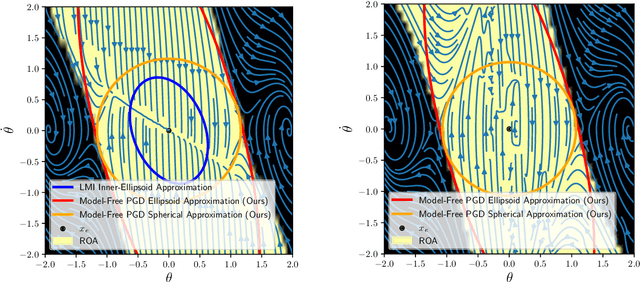
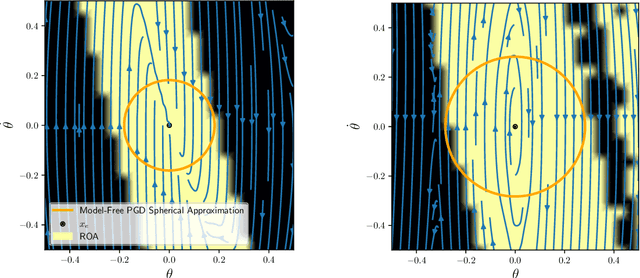
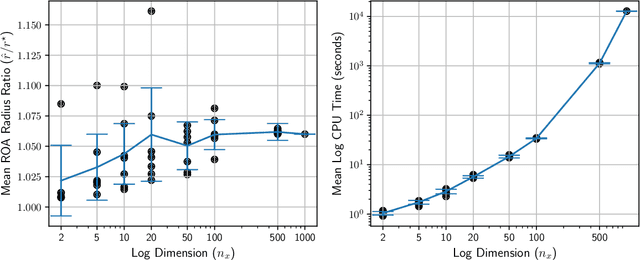
Many existing region-of-attraction (ROA) analysis tools find difficulty in addressing feedback systems with large-scale neural network (NN) policies and/or high-dimensional sensing modalities such as cameras. In this paper, we tailor the projected gradient descent (PGD) attack method developed in the adversarial learning community as a general-purpose ROA analysis tool for large-scale nonlinear systems and end-to-end perception-based control. We show that the ROA analysis can be approximated as a constrained maximization problem whose goal is to find the worst-case initial condition which shifts the terminal state the most. Then we present two PGD-based iterative methods which can be used to solve the resultant constrained maximization problem. Our analysis is not based on Lyapunov theory, and hence requires minimum information of the problem structures. In the model-based setting, we show that the PGD updates can be efficiently performed using back-propagation. In the model-free setting (which is more relevant to ROA analysis of perception-based control), we propose a finite-difference PGD estimate which is general and only requires a black-box simulator for generating the trajectories of the closed-loop system given any initial state. We demonstrate the scalability and generality of our analysis tool on several numerical examples with large-scale NN policies and high-dimensional image observations. We believe that our proposed analysis serves as a meaningful initial step toward further understanding of closed-loop stability of large-scale nonlinear systems and perception-based control.

Model-Free $μ$ Synthesis via Adversarial Reinforcement Learning

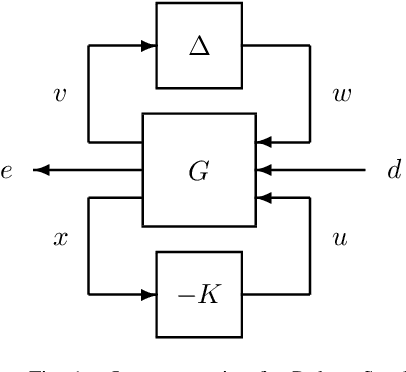
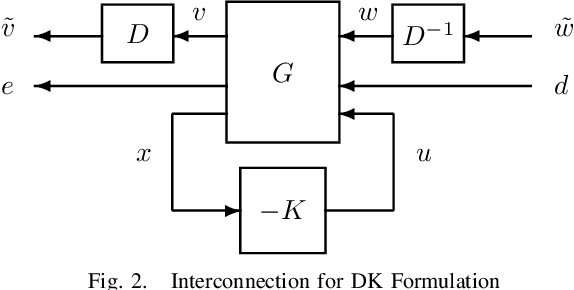
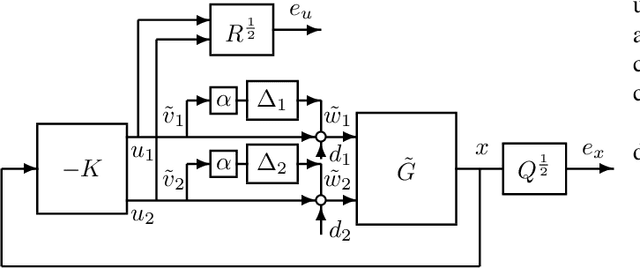
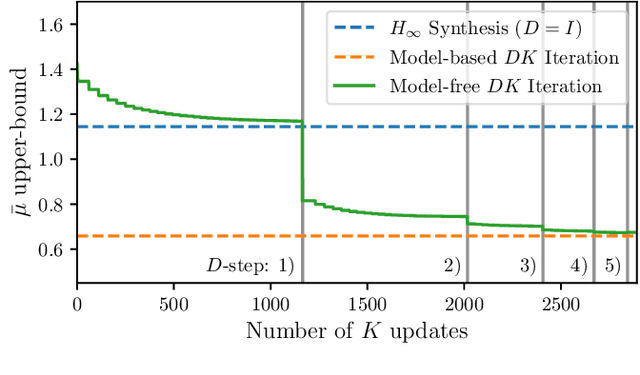
Motivated by the recent empirical success of policy-based reinforcement learning (RL), there has been a research trend studying the performance of policy-based RL methods on standard control benchmark problems. In this paper, we examine the effectiveness of policy-based RL methods on an important robust control problem, namely $\mu$ synthesis. We build a connection between robust adversarial RL and $\mu$ synthesis, and develop a model-free version of the well-known $DK$-iteration for solving state-feedback $\mu$ synthesis with static $D$-scaling. In the proposed algorithm, the $K$ step mimics the classical central path algorithm via incorporating a recently-developed double-loop adversarial RL method as a subroutine, and the $D$ step is based on model-free finite difference approximation. Extensive numerical study is also presented to demonstrate the utility of our proposed model-free algorithm. Our study sheds new light on the connections between adversarial RL and robust control.

Forced Variational Integrator Networks for Prediction and Control of Mechanical Systems

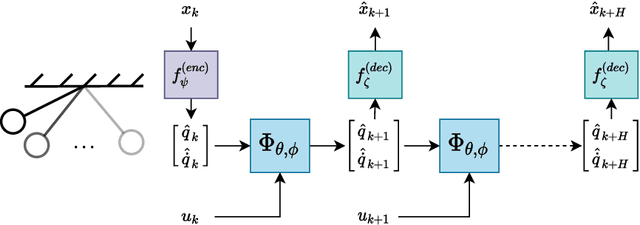
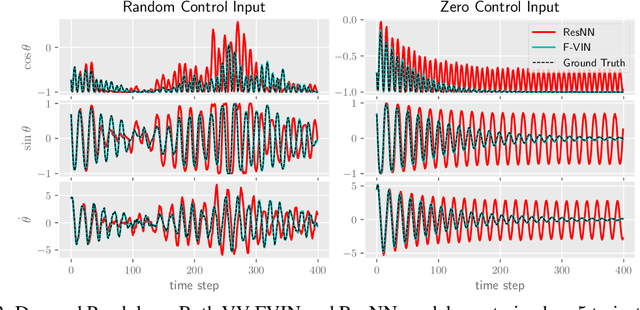
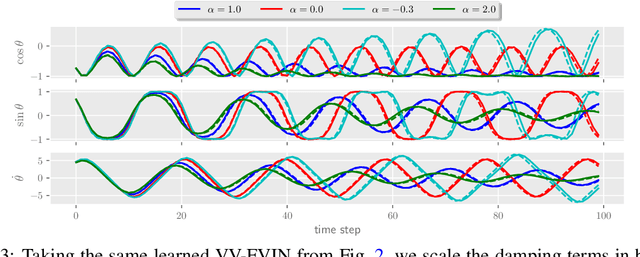
As deep learning becomes more prevalent for prediction and control of real physical systems, it is important that these overparameterized models are consistent with physically plausible dynamics. This elicits a problem with how much inductive bias to impose on the model through known physical parameters and principles to reduce complexity of the learning problem to give us more reliable predictions. Recent work employs discrete variational integrators parameterized as a neural network architecture to learn conservative Lagrangian systems. The learned model captures and enforces global energy preserving properties of the system from very few trajectories. However, most real systems are inherently non-conservative and, in practice, we would also like to apply actuation. In this paper we extend this paradigm to account for general forcing (e.g. control input and damping) via discrete d'Alembert's principle which may ultimately be used for control applications. We show that this forced variational integrator networks (FVIN) architecture allows us to accurately account for energy dissipation and external forcing while still capturing the true underlying energy-based passive dynamics. We show that in application this can result in highly-data efficient model-based control and can predict on real non-conservative systems.

On Imitation Learning of Linear Control Policies: Enforcing Stability and Robustness Constraints via LMI Conditions

When applying imitation learning techniques to fit a policy from expert demonstrations, one can take advantage of prior stability/robustness assumptions on the expert's policy and incorporate such control-theoretic prior knowledge explicitly into the learning process. In this paper, we formulate the imitation learning of linear policies as a constrained optimization problem, and present efficient methods which can be used to enforce stability and robustness constraints during the learning processes. Specifically, we show that one can guarantee the closed-loop stability and robustness by posing linear matrix inequality (LMI) constraints on the fitted policy. Then both the projected gradient descent method and the alternating direction method of multipliers (ADMM) method can be applied to solve the resulting constrained policy fitting problem. Finally, we provide numerical results to demonstrate the effectiveness of our methods in producing linear polices with various stability and robustness guarantees.

Learning Latent State Spaces for Planning through Reward Prediction

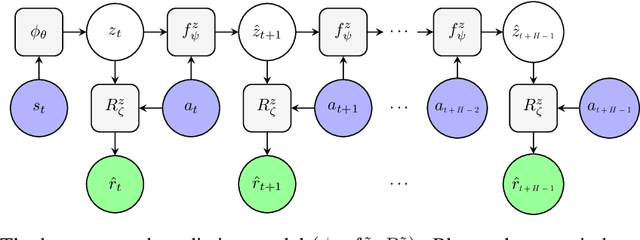
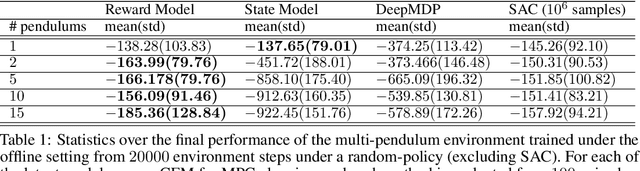
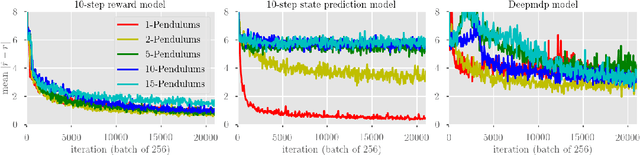
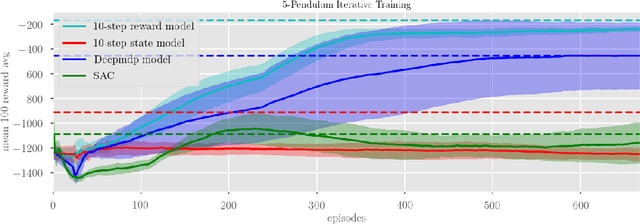
Model-based reinforcement learning methods typically learn models for high-dimensional state spaces by aiming to reconstruct and predict the original observations. However, drawing inspiration from model-free reinforcement learning, we propose learning a latent dynamics model directly from rewards. In this work, we introduce a model-based planning framework which learns a latent reward prediction model and then plans in the latent state-space. The latent representation is learned exclusively from multi-step reward prediction which we show to be the only necessary information for successful planning. With this framework, we are able to benefit from the concise model-free representation, while still enjoying the data-efficiency of model-based algorithms. We demonstrate our framework in multi-pendulum and multi-cheetah environments where several pendulums or cheetahs are shown to the agent but only one of which produces rewards. In these environments, it is important for the agent to construct a concise latent representation to filter out irrelevant observations. We find that our method can successfully learn an accurate latent reward prediction model in the presence of the irrelevant information while existing model-based methods fail. Planning in the learned latent state-space shows strong performance and high sample efficiency over model-free and model-based baselines.

Learning to Cope with Adversarial Attacks

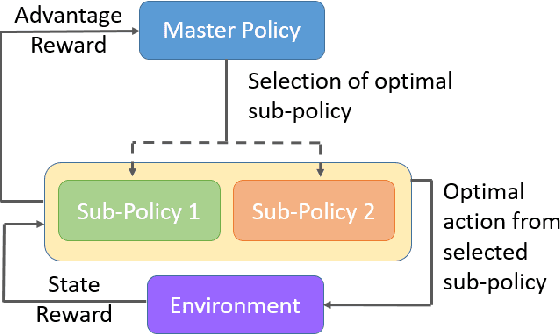
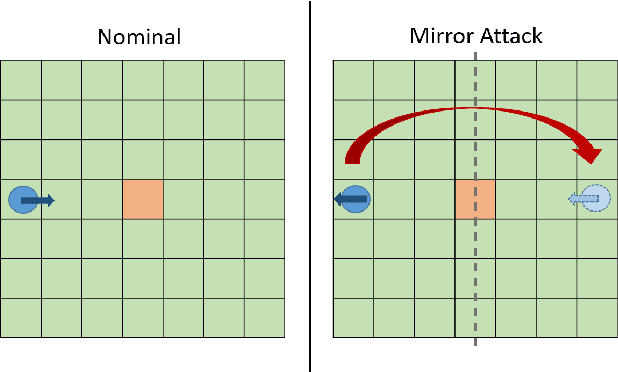
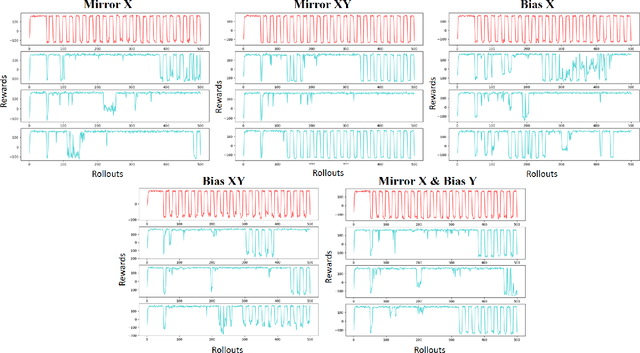
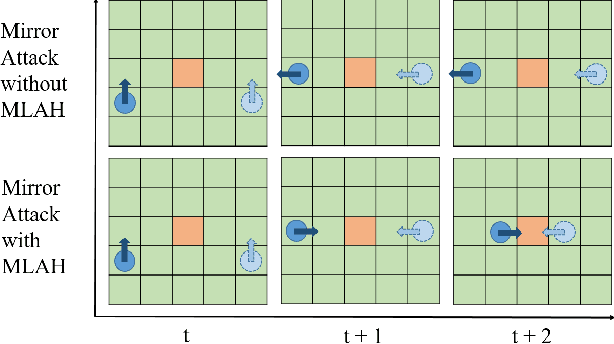
The security of Deep Reinforcement Learning (Deep RL) algorithms deployed in real life applications are of a primary concern. In particular, the robustness of RL agents in cyber-physical systems against adversarial attacks are especially vital since the cost of a malevolent intrusions can be extremely high. Studies have shown Deep Neural Networks (DNN), which forms the core decision-making unit in most modern RL algorithms, are easily subjected to adversarial attacks. Hence, it is imperative that RL agents deployed in real-life applications have the capability to detect and mitigate adversarial attacks in an online fashion. An example of such a framework is the Meta-Learned Advantage Hierarchy (MLAH) agent that utilizes a meta-learning framework to learn policies robustly online. Since the mechanism of this framework are still not fully explored, we conducted multiple experiments to better understand the framework's capabilities and limitations. Our results shows that the MLAH agent exhibits interesting coping behaviors when subjected to different adversarial attacks to maintain a nominal reward. Additionally, the framework exhibits a hierarchical coping capability, based on the adaptability of the Master policy and sub-policies themselves. From empirical results, we also observed that as the interval of adversarial attacks increase, the MLAH agent can maintain a higher distribution of rewards, though at the cost of higher instabilities.