Revisiting PGD Attacks for Stability Analysis of Large-Scale Nonlinear Systems and Perception-Based Control

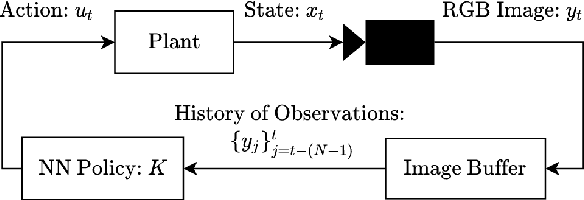
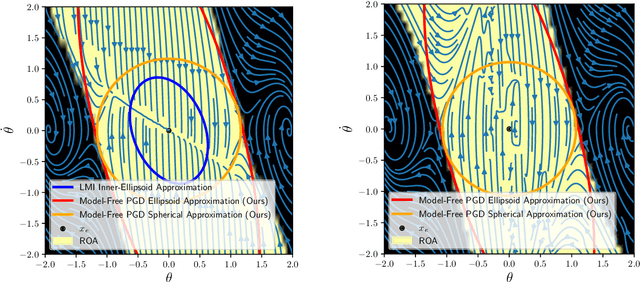
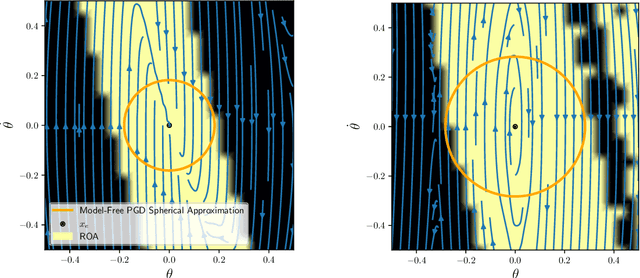
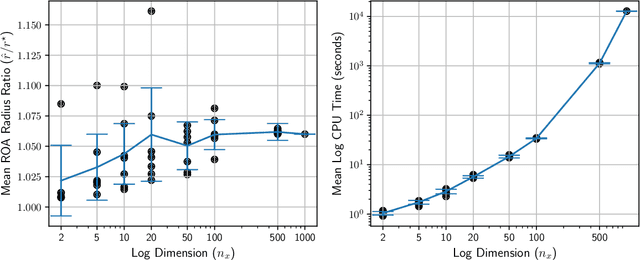
Many existing region-of-attraction (ROA) analysis tools find difficulty in addressing feedback systems with large-scale neural network (NN) policies and/or high-dimensional sensing modalities such as cameras. In this paper, we tailor the projected gradient descent (PGD) attack method developed in the adversarial learning community as a general-purpose ROA analysis tool for large-scale nonlinear systems and end-to-end perception-based control. We show that the ROA analysis can be approximated as a constrained maximization problem whose goal is to find the worst-case initial condition which shifts the terminal state the most. Then we present two PGD-based iterative methods which can be used to solve the resultant constrained maximization problem. Our analysis is not based on Lyapunov theory, and hence requires minimum information of the problem structures. In the model-based setting, we show that the PGD updates can be efficiently performed using back-propagation. In the model-free setting (which is more relevant to ROA analysis of perception-based control), we propose a finite-difference PGD estimate which is general and only requires a black-box simulator for generating the trajectories of the closed-loop system given any initial state. We demonstrate the scalability and generality of our analysis tool on several numerical examples with large-scale NN policies and high-dimensional image observations. We believe that our proposed analysis serves as a meaningful initial step toward further understanding of closed-loop stability of large-scale nonlinear systems and perception-based control.