A Complete Set of Quadratic Constraints For Repeated ReLU

This paper derives a complete set of quadratic constraints (QCs) for the repeated ReLU. The complete set of QCs is described by a collection of $2^{n_v}$ matrix copositivity conditions where $n_v$ is the dimension of the repeated ReLU. We also show that only two functions satisfy all QCs in our complete set: the repeated ReLU and a repeated "flipped" ReLU. Thus our complete set of QCs bounds the repeated ReLU as tight as possible up to the sign invariance inherent in quadratic forms. We derive a similar complete set of incremental QCs for repeated ReLU, which can potentially lead to less conservative Lipschitz bounds for ReLU networks than the standard LipSDP approach. Finally, we illustrate the use of the complete set of QCs to assess stability and performance for recurrent neural networks with ReLU activation functions. The stability/performance condition combines Lyapunov/dissipativity theory with the QCs for repeated ReLU. A numerical implementation is given and demonstrated via a simple example.

Stability and Performance Analysis of Discrete-Time ReLU Recurrent Neural Networks

This paper presents sufficient conditions for the stability and $\ell_2$-gain performance of recurrent neural networks (RNNs) with ReLU activation functions. These conditions are derived by combining Lyapunov/dissipativity theory with Quadratic Constraints (QCs) satisfied by repeated ReLUs. We write a general class of QCs for repeated RELUs using known properties for the scalar ReLU. Our stability and performance condition uses these QCs along with a "lifted" representation for the ReLU RNN. We show that the positive homogeneity property satisfied by a scalar ReLU does not expand the class of QCs for the repeated ReLU. We present examples to demonstrate the stability / performance condition and study the effect of the lifting horizon.

Synthesizing Neural Network Controllers with Closed-Loop Dissipativity Guarantees

In this paper, a method is presented to synthesize neural network controllers such that the feedback system of plant and controller is dissipative, certifying performance requirements such as L2 gain bounds. The class of plants considered is that of linear time-invariant (LTI) systems interconnected with an uncertainty, including nonlinearities treated as an uncertainty for convenience of analysis. The uncertainty of the plant and the nonlinearities of the neural network are both described using integral quadratic constraints (IQCs). First, a dissipativity condition is derived for uncertain LTI systems. Second, this condition is used to construct a linear matrix inequality (LMI) which can be used to synthesize neural network controllers. Finally, this convex condition is used in a projection-based training method to synthesize neural network controllers with dissipativity guarantees. Numerical examples on an inverted pendulum and a flexible rod on a cart are provided to demonstrate the effectiveness of this approach.

Capabilities of Large Language Models in Control Engineering: A Benchmark Study on GPT-4, Claude 3 Opus, and Gemini 1.0 Ultra

In this paper, we explore the capabilities of state-of-the-art large language models (LLMs) such as GPT-4, Claude 3 Opus, and Gemini 1.0 Ultra in solving undergraduate-level control problems. Controls provides an interesting case study for LLM reasoning due to its combination of mathematical theory and engineering design. We introduce ControlBench, a benchmark dataset tailored to reflect the breadth, depth, and complexity of classical control design. We use this dataset to study and evaluate the problem-solving abilities of these LLMs in the context of control engineering. We present evaluations conducted by a panel of human experts, providing insights into the accuracy, reasoning, and explanatory prowess of LLMs in control engineering. Our analysis reveals the strengths and limitations of each LLM in the context of classical control, and our results imply that Claude 3 Opus has become the state-of-the-art LLM for solving undergraduate control problems. Our study serves as an initial step towards the broader goal of employing artificial general intelligence in control engineering.

Model-Free $μ$-Synthesis: A Nonsmooth Optimization Perspective

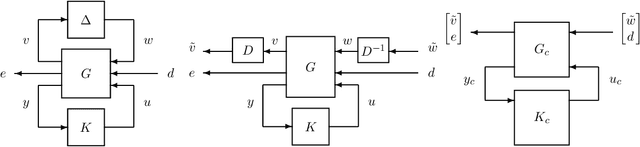
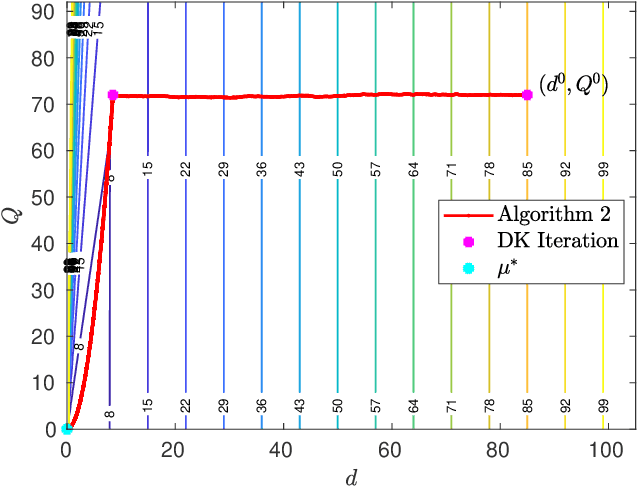
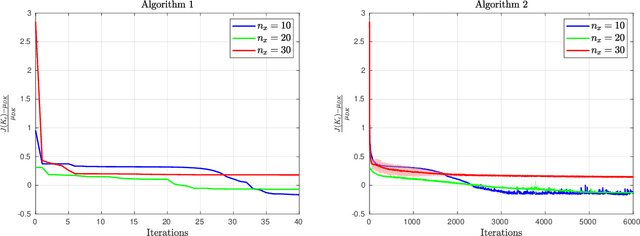
In this paper, we revisit model-free policy search on an important robust control benchmark, namely $\mu$-synthesis. In the general output-feedback setting, there do not exist convex formulations for this problem, and hence global optimality guarantees are not expected. Apkarian (2011) presented a nonconvex nonsmooth policy optimization approach for this problem, and achieved state-of-the-art design results via using subgradient-based policy search algorithms which generate update directions in a model-based manner. Despite the lack of convexity and global optimality guarantees, these subgradient-based policy search methods have led to impressive numerical results in practice. Built upon such a policy optimization persepctive, our paper extends these subgradient-based search methods to a model-free setting. Specifically, we examine the effectiveness of two model-free policy optimization strategies: the model-free non-derivative sampling method and the zeroth-order policy search with uniform smoothing. We performed an extensive numerical study to demonstrate that both methods consistently replicate the design outcomes achieved by their model-based counterparts. Additionally, we provide some theoretical justifications showing that convergence guarantees to stationary points can be established for our model-free $\mu$-synthesis under some assumptions related to the coerciveness of the cost function. Overall, our results demonstrate that derivative-free policy optimization offers a competitive and viable approach for solving general output-feedback $\mu$-synthesis problems in the model-free setting.

Synthesis of Stabilizing Recurrent Equilibrium Network Controllers

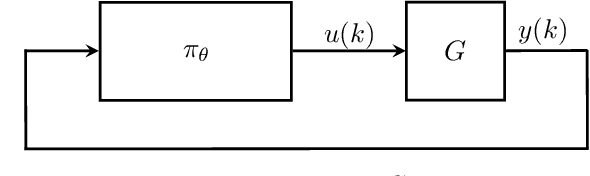
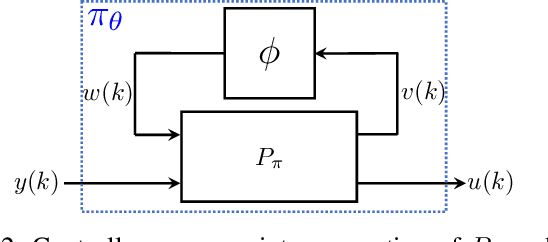
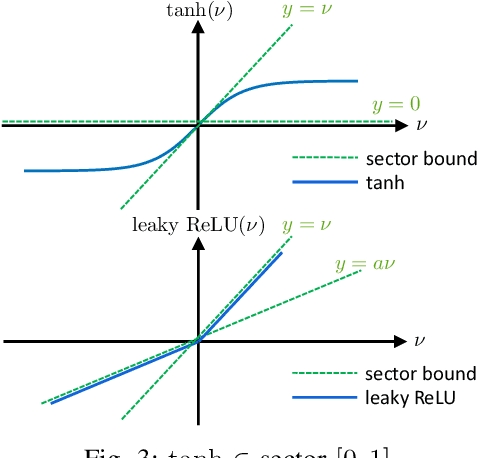
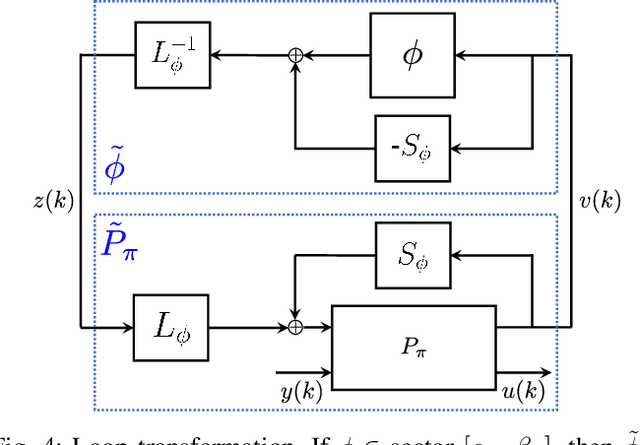
We propose a parameterization of a nonlinear dynamic controller based on the recurrent equilibrium network, a generalization of the recurrent neural network. We derive constraints on the parameterization under which the controller guarantees exponential stability of a partially observed dynamical system with sector-bounded nonlinearities. Finally, we present a method to synthesize this controller using projected policy gradient methods to maximize a reward function with arbitrary structure. The projection step involves the solution of convex optimization problems. We demonstrate the proposed method with simulated examples of controlling nonlinear plants, including plants modeled with neural networks.

Revisiting PGD Attacks for Stability Analysis of Large-Scale Nonlinear Systems and Perception-Based Control

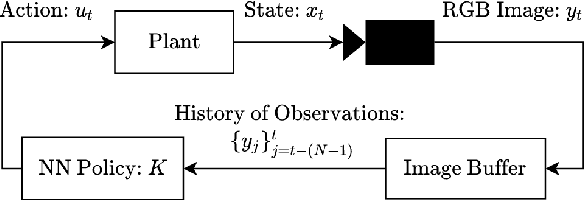
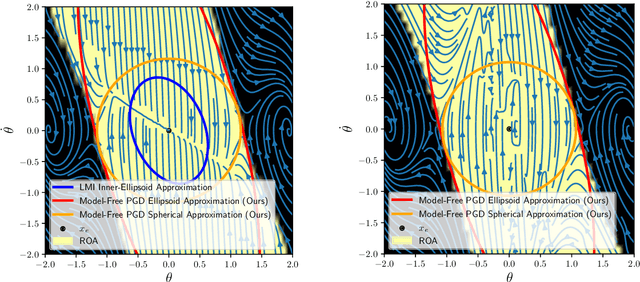
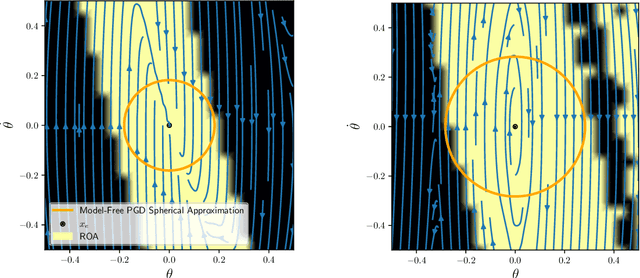
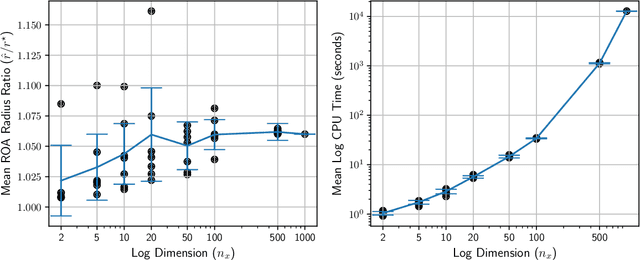
Many existing region-of-attraction (ROA) analysis tools find difficulty in addressing feedback systems with large-scale neural network (NN) policies and/or high-dimensional sensing modalities such as cameras. In this paper, we tailor the projected gradient descent (PGD) attack method developed in the adversarial learning community as a general-purpose ROA analysis tool for large-scale nonlinear systems and end-to-end perception-based control. We show that the ROA analysis can be approximated as a constrained maximization problem whose goal is to find the worst-case initial condition which shifts the terminal state the most. Then we present two PGD-based iterative methods which can be used to solve the resultant constrained maximization problem. Our analysis is not based on Lyapunov theory, and hence requires minimum information of the problem structures. In the model-based setting, we show that the PGD updates can be efficiently performed using back-propagation. In the model-free setting (which is more relevant to ROA analysis of perception-based control), we propose a finite-difference PGD estimate which is general and only requires a black-box simulator for generating the trajectories of the closed-loop system given any initial state. We demonstrate the scalability and generality of our analysis tool on several numerical examples with large-scale NN policies and high-dimensional image observations. We believe that our proposed analysis serves as a meaningful initial step toward further understanding of closed-loop stability of large-scale nonlinear systems and perception-based control.

Model-Free $μ$ Synthesis via Adversarial Reinforcement Learning

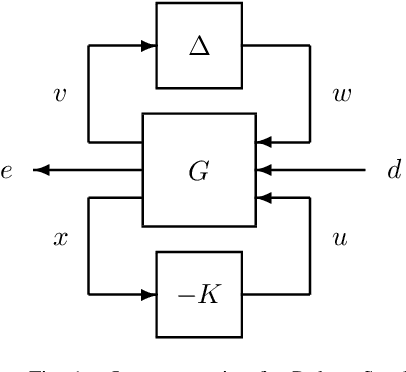
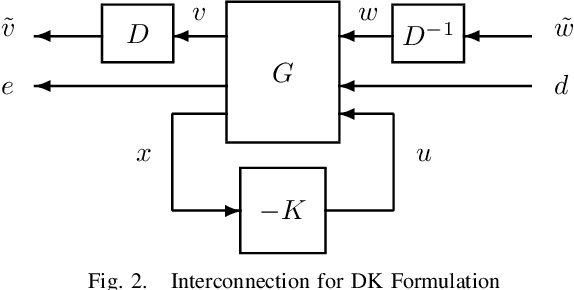
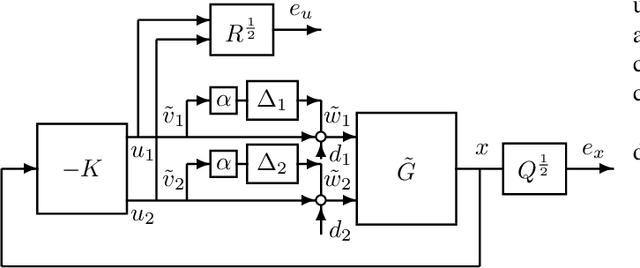
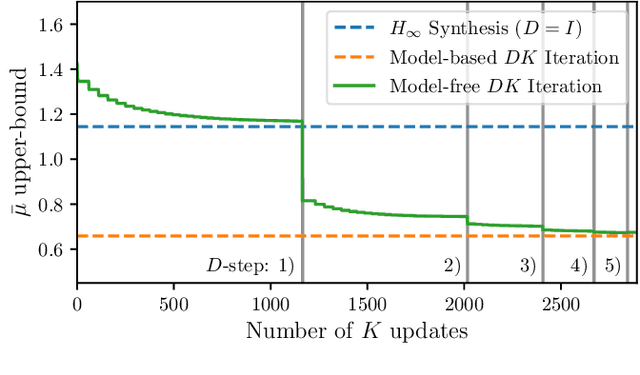
Motivated by the recent empirical success of policy-based reinforcement learning (RL), there has been a research trend studying the performance of policy-based RL methods on standard control benchmark problems. In this paper, we examine the effectiveness of policy-based RL methods on an important robust control problem, namely $\mu$ synthesis. We build a connection between robust adversarial RL and $\mu$ synthesis, and develop a model-free version of the well-known $DK$-iteration for solving state-feedback $\mu$ synthesis with static $D$-scaling. In the proposed algorithm, the $K$ step mimics the classical central path algorithm via incorporating a recently-developed double-loop adversarial RL method as a subroutine, and the $D$ step is based on model-free finite difference approximation. Extensive numerical study is also presented to demonstrate the utility of our proposed model-free algorithm. Our study sheds new light on the connections between adversarial RL and robust control.

Robustness against Adversarial Attacks in Neural Networks using Incremental Dissipativity

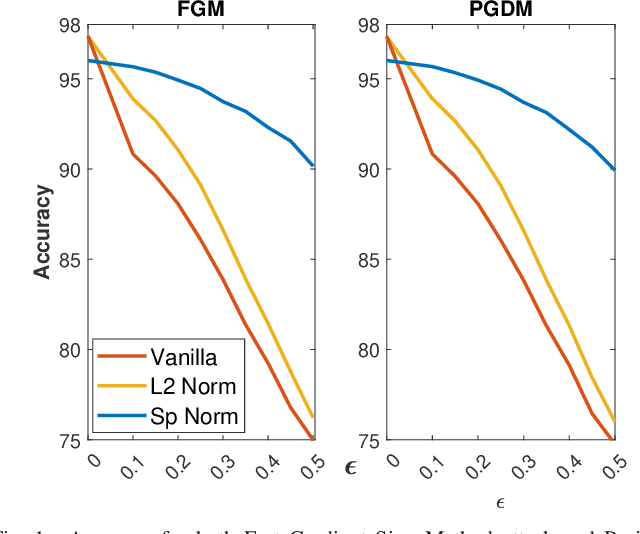
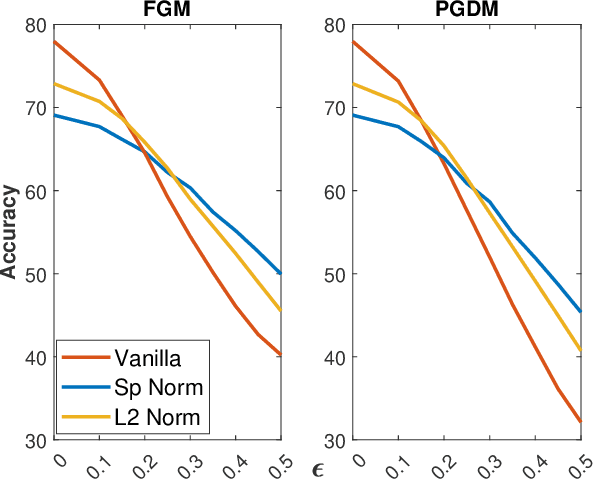
Adversarial examples can easily degrade the classification performance in neural networks. Empirical methods for promoting robustness to such examples have been proposed, but often lack both analytical insights and formal guarantees. Recently, some robustness certificates have appeared in the literature based on system theoretic notions. This work proposes an incremental dissipativity-based robustness certificate for neural networks in the form of a linear matrix inequality for each layer. We also propose an equivalent spectral norm bound for this certificate which is scalable to neural networks with multiple layers. We demonstrate the improved performance against adversarial attacks on a feed-forward neural network trained on MNIST and an Alexnet trained using CIFAR-10.

Recurrent Neural Network Controllers Synthesis with Stability Guarantees for Partially Observed Systems

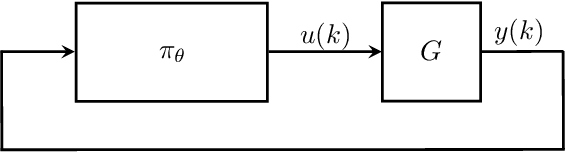
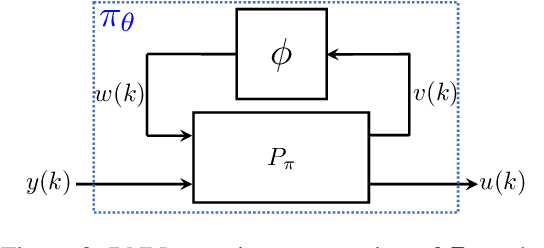
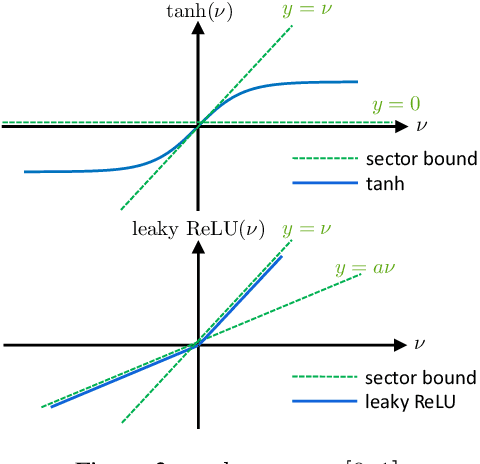
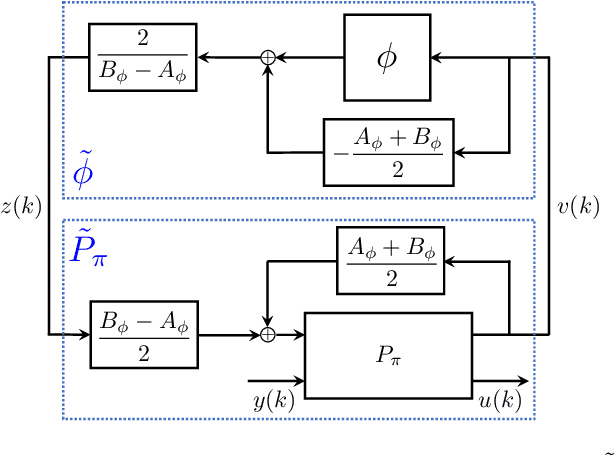
Neural network controllers have become popular in control tasks thanks to their flexibility and expressivity. Stability is a crucial property for safety-critical dynamical systems, while stabilization of partially observed systems, in many cases, requires controllers to retain and process long-term memories of the past. We consider the important class of recurrent neural networks (RNN) as dynamic controllers for nonlinear uncertain partially-observed systems, and derive convex stability conditions based on integral quadratic constraints, S-lemma and sequential convexification. To ensure stability during the learning and control process, we propose a projected policy gradient method that iteratively enforces the stability conditions in the reparametrized space taking advantage of mild additional information on system dynamics. Numerical experiments show that our method learns stabilizing controllers while using fewer samples and achieving higher final performance compared with policy gradient.