Synthesis of Stabilizing Recurrent Equilibrium Network Controllers
Paper and Code
Mar 31, 2022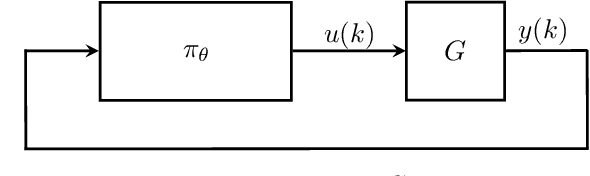
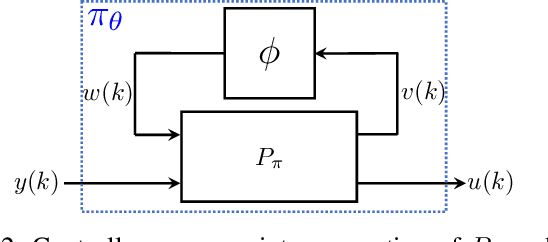
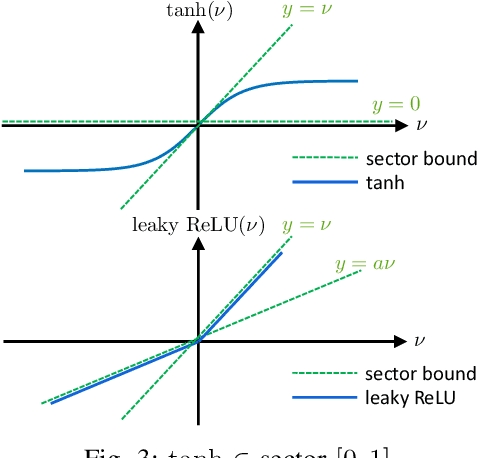
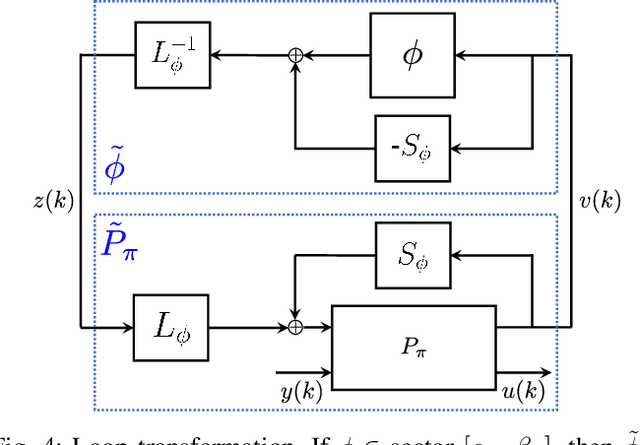
We propose a parameterization of a nonlinear dynamic controller based on the recurrent equilibrium network, a generalization of the recurrent neural network. We derive constraints on the parameterization under which the controller guarantees exponential stability of a partially observed dynamical system with sector-bounded nonlinearities. Finally, we present a method to synthesize this controller using projected policy gradient methods to maximize a reward function with arbitrary structure. The projection step involves the solution of convex optimization problems. We demonstrate the proposed method with simulated examples of controlling nonlinear plants, including plants modeled with neural networks.
* Submitted to IEEE CDC 2022. arXiv admin note: text overlap with
arXiv:2109.03861
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge