Synthesizing Neural Network Controllers with Closed-Loop Dissipativity Guarantees

In this paper, a method is presented to synthesize neural network controllers such that the feedback system of plant and controller is dissipative, certifying performance requirements such as L2 gain bounds. The class of plants considered is that of linear time-invariant (LTI) systems interconnected with an uncertainty, including nonlinearities treated as an uncertainty for convenience of analysis. The uncertainty of the plant and the nonlinearities of the neural network are both described using integral quadratic constraints (IQCs). First, a dissipativity condition is derived for uncertain LTI systems. Second, this condition is used to construct a linear matrix inequality (LMI) which can be used to synthesize neural network controllers. Finally, this convex condition is used in a projection-based training method to synthesize neural network controllers with dissipativity guarantees. Numerical examples on an inverted pendulum and a flexible rod on a cart are provided to demonstrate the effectiveness of this approach.

Exploiting Symmetry in Dynamics for Model-Based Reinforcement Learning with Asymmetric Rewards

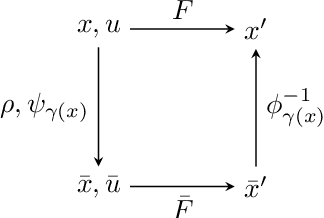
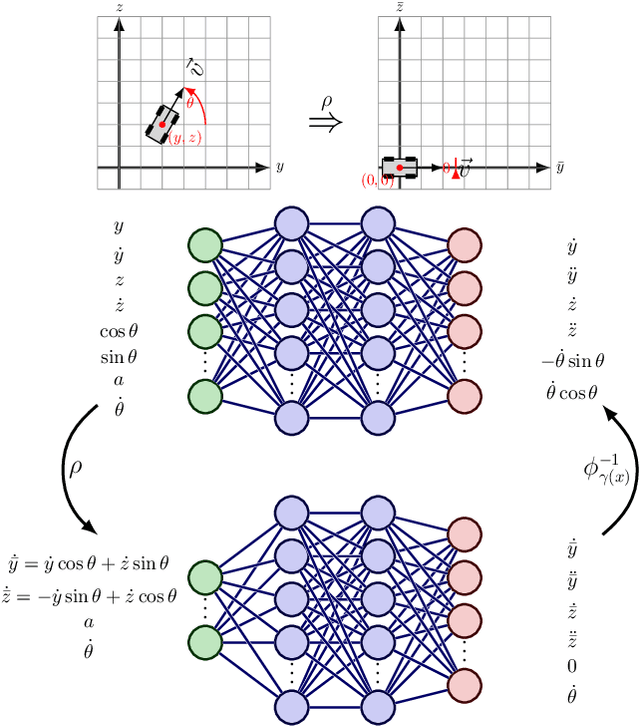
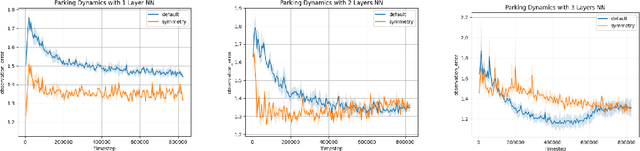
Recent work in reinforcement learning has leveraged symmetries in the model to improve sample efficiency in training a policy. A commonly used simplifying assumption is that the dynamics and reward both exhibit the same symmetry. However, in many real-world environments, the dynamical model exhibits symmetry independent of the reward model: the reward may not satisfy the same symmetries as the dynamics. In this paper, we investigate scenarios where only the dynamics are assumed to exhibit symmetry, extending the scope of problems in reinforcement learning and learning in control theory where symmetry techniques can be applied. We use Cartan's moving frame method to introduce a technique for learning dynamics which, by construction, exhibit specified symmetries. We demonstrate through numerical experiments that the proposed method learns a more accurate dynamical model.

Exact Recovery for System Identification with More Corrupt Data than Clean Data

In this paper, we study the system identification problem for linear discrete-time systems under adversaries and analyze two lasso-type estimators. We study both asymptotic and non-asymptotic properties of these estimators in two separate scenarios, corresponding to deterministic and stochastic models for the attack times. Since the samples collected from the system are correlated, the existing results on lasso are not applicable. We show that when the system is stable and the attacks are injected periodically, the sample complexity for the exact recovery of the system dynamics is O(n), where n is the dimension of the states. When the adversarial attacks occur at each time instance with probability p, the required sample complexity for the exact recovery scales as O(\log(n)p/(1-p)^2). This result implies the almost sure convergence to the true system dynamics under the asymptotic regime. As a by-product, even when more than half of the data is compromised, our estimators still learn the system correctly. This paper provides the first mathematical guarantee in the literature on learning from correlated data for dynamical systems in the case when there is less clean data than corrupt data.

Synthesis of Stabilizing Recurrent Equilibrium Network Controllers

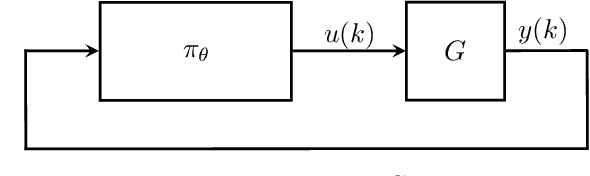
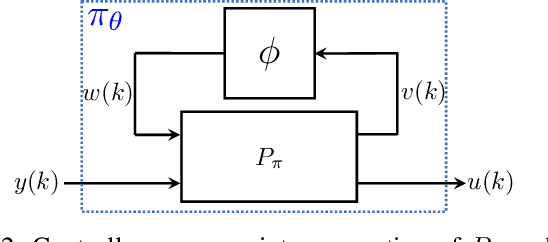
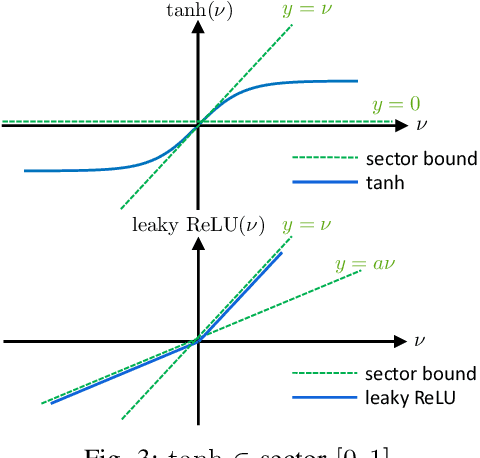
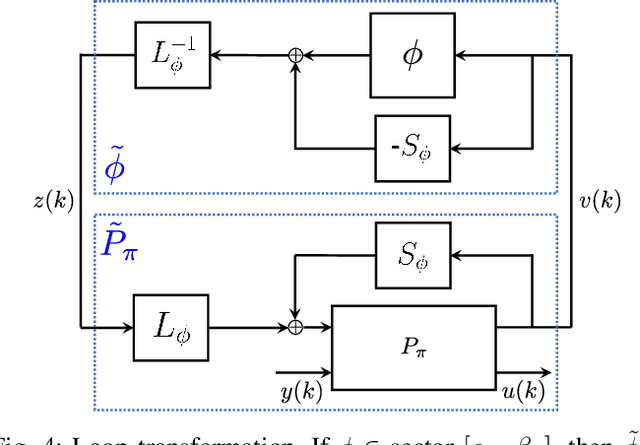
We propose a parameterization of a nonlinear dynamic controller based on the recurrent equilibrium network, a generalization of the recurrent neural network. We derive constraints on the parameterization under which the controller guarantees exponential stability of a partially observed dynamical system with sector-bounded nonlinearities. Finally, we present a method to synthesize this controller using projected policy gradient methods to maximize a reward function with arbitrary structure. The projection step involves the solution of convex optimization problems. We demonstrate the proposed method with simulated examples of controlling nonlinear plants, including plants modeled with neural networks.

Data-Driven Reachability analysis and Support set Estimation with Christoffel Functions

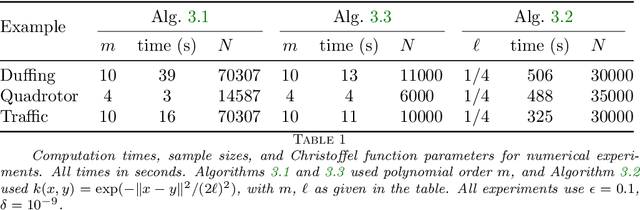
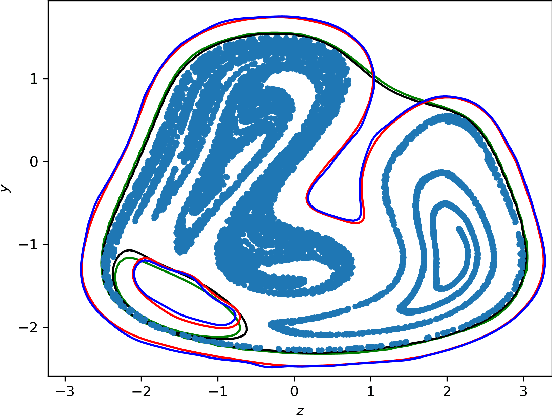
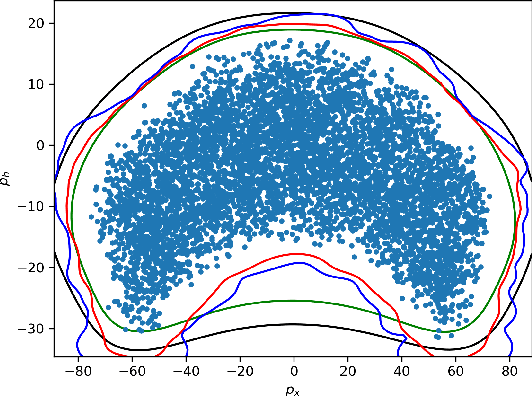
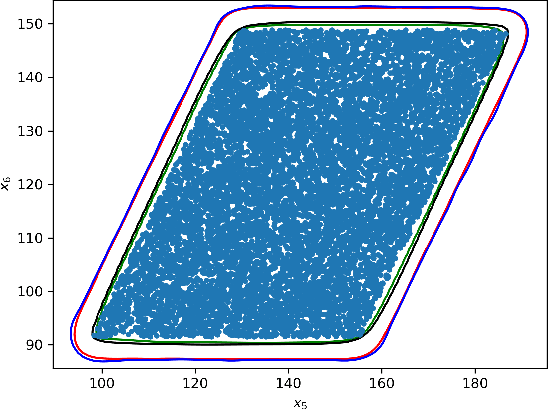
We present algorithms for estimating the forward reachable set of a dynamical system using only a finite collection of independent and identically distributed samples. The produced estimate is the sublevel set of a function called an empirical inverse Christoffel function: empirical inverse Christoffel functions are known to provide good approximations to the support of probability distributions. In addition to reachability analysis, the same approach can be applied to general problems of estimating the support of a random variable, which has applications in data science towards detection of novelties and outliers in data sets. In applications where safety is a concern, having a guarantee of accuracy that holds on finite data sets is critical. In this paper, we prove such bounds for our algorithms under the Probably Approximately Correct (PAC) framework. In addition to applying classical Vapnik-Chervonenkis (VC) dimension bound arguments, we apply the PAC-Bayes theorem by leveraging a formal connection between kernelized empirical inverse Christoffel functions and Gaussian process regression models. The bound based on PAC-Bayes applies to a more general class of Christoffel functions than the VC dimension argument, and achieves greater sample efficiency in experiments.

Recurrent Neural Network Controllers Synthesis with Stability Guarantees for Partially Observed Systems

Neural network controllers have become popular in control tasks thanks to their flexibility and expressivity. Stability is a crucial property for safety-critical dynamical systems, while stabilization of partially observed systems, in many cases, requires controllers to retain and process long-term memories of the past. We consider the important class of recurrent neural networks (RNN) as dynamic controllers for nonlinear uncertain partially-observed systems, and derive convex stability conditions based on integral quadratic constraints, S-lemma and sequential convexification. To ensure stability during the learning and control process, we propose a projected policy gradient method that iteratively enforces the stability conditions in the reparametrized space taking advantage of mild additional information on system dynamics. Numerical experiments show that our method learns stabilizing controllers while using fewer samples and achieving higher final performance compared with policy gradient.

Symbolic Abstractions From Data: A PAC Learning Approach

Symbolic control techniques aim to satisfy complex logic specifications. A critical step in these techniques is the construction of a symbolic (discrete) abstraction, a finite-state system whose behaviour mimics that of a given continuous-state system. The methods used to compute symbolic abstractions, however, require knowledge of an accurate closed-form model. To generalize them to systems with unknown dynamics, we present a new data-driven approach that does not require closed-form dynamics, instead relying only the ability to evaluate successors of each state under given inputs. To provide guarantees for the learned abstraction, we use the Probably Approximately Correct (PAC) statistical framework. We first introduce a PAC-style behavioural relationship and an appropriate refinement procedure. We then show how the symbolic abstraction can be constructed to satisfy this new behavioural relationship. Moreover, we provide PAC bounds that dictate the number of data required to guarantee a prescribed level of accuracy and confidence. Finally, we present an illustrative example.

Co-design of Control and Planning for Multi-rotor UAVs with Signal Temporal Logic Specifications

Urban Air Mobility (UAM), or the scenario where multiple manned and Unmanned Aerial Vehicles (UAVs) carry out various tasks over urban airspaces, is a transportation concept of the future that is gaining prominence. UAM missions with complex spatial, temporal and reactive requirements can be succinctly represented using Signal Temporal Logic (STL), a behavioral specification language. However, planning and control of systems with STL specifications is computationally intensive, usually resulting in planning approaches that do not guarantee dynamical feasibility, or control approaches that cannot handle complex STL specifications. Here, we present an approach to co-design the planner and control such that a given STL specification (possibly over multiple UAVs) is satisfied with trajectories that are dynamically feasible and our controller can track them with a bounded tracking-error that the planner accounts for. The tracking controller is formulated for the non-linear dynamics of the individual UAVs, and the tracking error bound is computed for this controller when the trajectories satisfy some kinematic constraints. We also augment an existing multi-UAV STL-based trajectory generator in order to generate trajectories that satisfy such constraints. We show that this co-design allows for trajectories that satisfy a given STL specification, and are also dynamically feasible in the sense that they can be tracked with bounded error. The applicability of this approach is demonstrated through simulations of multi-UAV missions.