Synthesizing Neural Network Controllers with Closed-Loop Dissipativity Guarantees

In this paper, a method is presented to synthesize neural network controllers such that the feedback system of plant and controller is dissipative, certifying performance requirements such as L2 gain bounds. The class of plants considered is that of linear time-invariant (LTI) systems interconnected with an uncertainty, including nonlinearities treated as an uncertainty for convenience of analysis. The uncertainty of the plant and the nonlinearities of the neural network are both described using integral quadratic constraints (IQCs). First, a dissipativity condition is derived for uncertain LTI systems. Second, this condition is used to construct a linear matrix inequality (LMI) which can be used to synthesize neural network controllers. Finally, this convex condition is used in a projection-based training method to synthesize neural network controllers with dissipativity guarantees. Numerical examples on an inverted pendulum and a flexible rod on a cart are provided to demonstrate the effectiveness of this approach.

Exploiting Symmetry in Dynamics for Model-Based Reinforcement Learning with Asymmetric Rewards

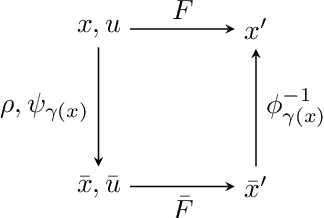
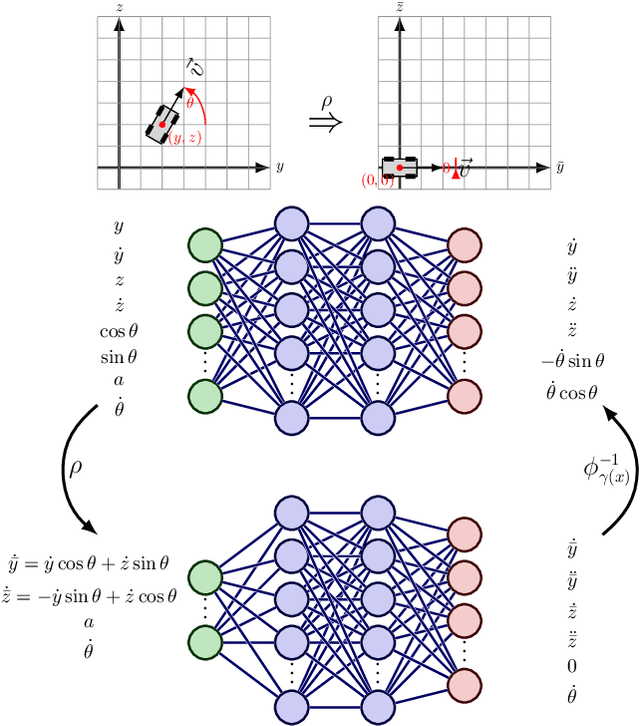
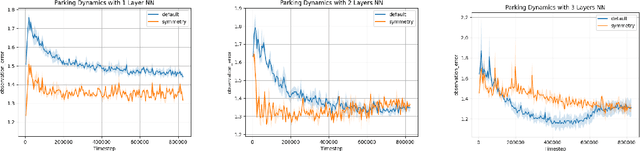
Recent work in reinforcement learning has leveraged symmetries in the model to improve sample efficiency in training a policy. A commonly used simplifying assumption is that the dynamics and reward both exhibit the same symmetry. However, in many real-world environments, the dynamical model exhibits symmetry independent of the reward model: the reward may not satisfy the same symmetries as the dynamics. In this paper, we investigate scenarios where only the dynamics are assumed to exhibit symmetry, extending the scope of problems in reinforcement learning and learning in control theory where symmetry techniques can be applied. We use Cartan's moving frame method to introduce a technique for learning dynamics which, by construction, exhibit specified symmetries. We demonstrate through numerical experiments that the proposed method learns a more accurate dynamical model.

Synthesis of Stabilizing Recurrent Equilibrium Network Controllers

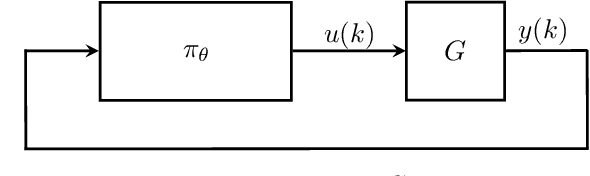
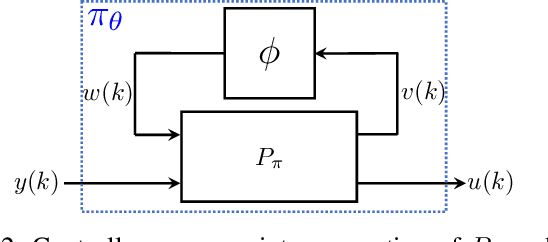
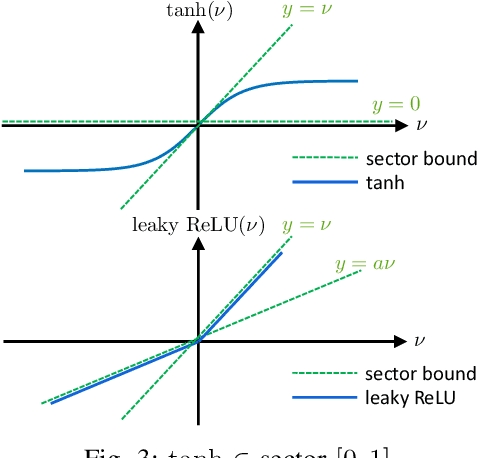
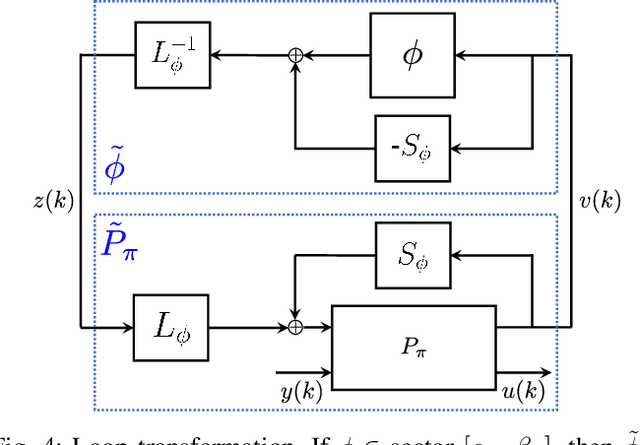
We propose a parameterization of a nonlinear dynamic controller based on the recurrent equilibrium network, a generalization of the recurrent neural network. We derive constraints on the parameterization under which the controller guarantees exponential stability of a partially observed dynamical system with sector-bounded nonlinearities. Finally, we present a method to synthesize this controller using projected policy gradient methods to maximize a reward function with arbitrary structure. The projection step involves the solution of convex optimization problems. We demonstrate the proposed method with simulated examples of controlling nonlinear plants, including plants modeled with neural networks.