The Extrapolation Power of Implicit Models

In this paper, we investigate the extrapolation capabilities of implicit deep learning models in handling unobserved data, where traditional deep neural networks may falter. Implicit models, distinguished by their adaptability in layer depth and incorporation of feedback within their computational graph, are put to the test across various extrapolation scenarios: out-of-distribution, geographical, and temporal shifts. Our experiments consistently demonstrate significant performance advantage with implicit models. Unlike their non-implicit counterparts, which often rely on meticulous architectural design for each task, implicit models demonstrate the ability to learn complex model structures without the need for task-specific design, highlighting their robustness in handling unseen data.

State-driven Implicit Modeling for Sparsity and Robustness in Neural Networks

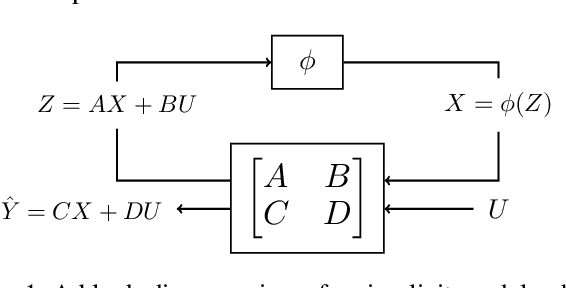
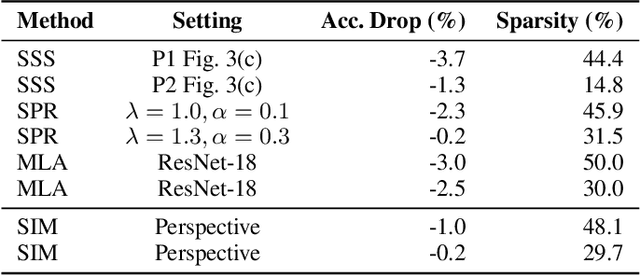
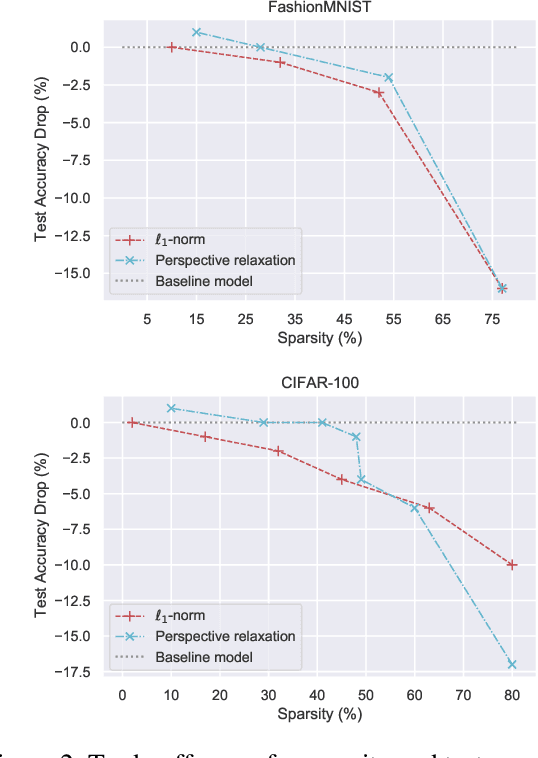
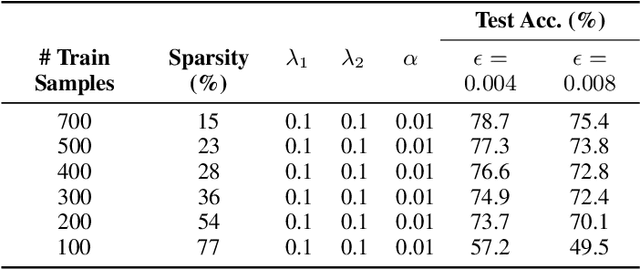
Implicit models are a general class of learning models that forgo the hierarchical layer structure typical in neural networks and instead define the internal states based on an ``equilibrium'' equation, offering competitive performance and reduced memory consumption. However, training such models usually relies on expensive implicit differentiation for backward propagation. In this work, we present a new approach to training implicit models, called State-driven Implicit Modeling (SIM), where we constrain the internal states and outputs to match that of a baseline model, circumventing costly backward computations. The training problem becomes convex by construction and can be solved in a parallel fashion, thanks to its decomposable structure. We demonstrate how the SIM approach can be applied to significantly improve sparsity (parameter reduction) and robustness of baseline models trained on FashionMNIST and CIFAR-100 datasets.

Sparse Optimization for Unsupervised Extractive Summarization of Long Documents with the Frank-Wolfe Algorithm

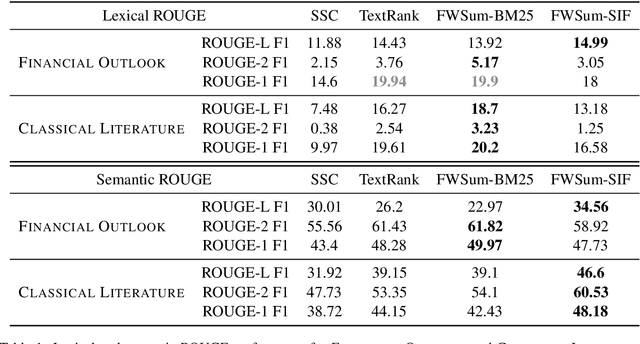
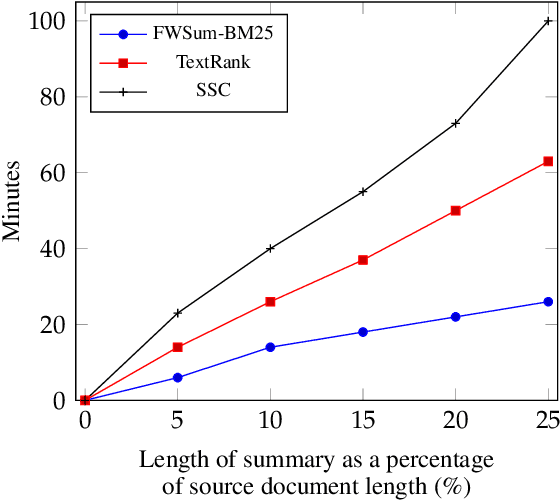
We address the problem of unsupervised extractive document summarization, especially for long documents. We model the unsupervised problem as a sparse auto-regression one and approximate the resulting combinatorial problem via a convex, norm-constrained problem. We solve it using a dedicated Frank-Wolfe algorithm. To generate a summary with $k$ sentences, the algorithm only needs to execute $\approx k$ iterations, making it very efficient. We explain how to avoid explicit calculation of the full gradient and how to include sentence embedding information. We evaluate our approach against two other unsupervised methods using both lexical (standard) ROUGE scores, as well as semantic (embedding-based) ones. Our method achieves better results with both datasets and works especially well when combined with embeddings for highly paraphrased summaries.

Data-Driven Reachability analysis and Support set Estimation with Christoffel Functions

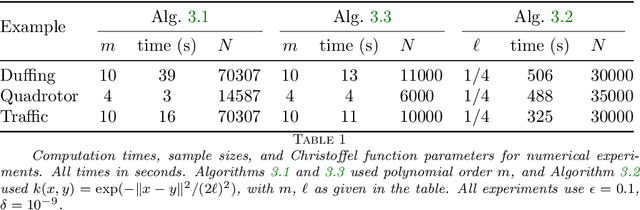
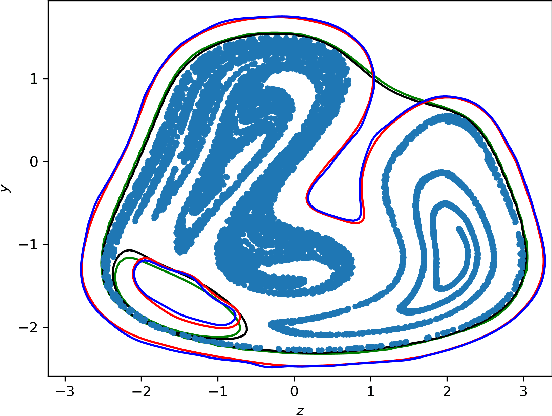
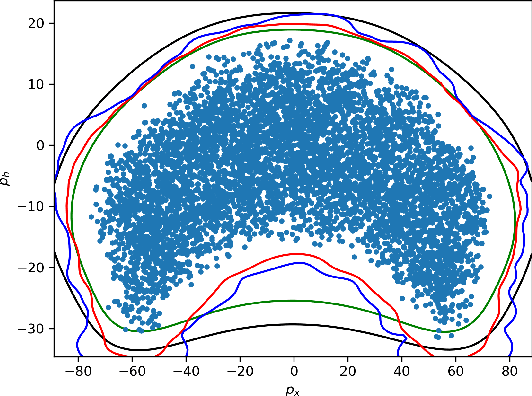
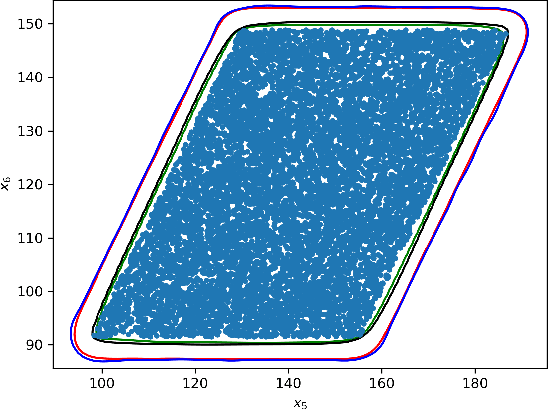
We present algorithms for estimating the forward reachable set of a dynamical system using only a finite collection of independent and identically distributed samples. The produced estimate is the sublevel set of a function called an empirical inverse Christoffel function: empirical inverse Christoffel functions are known to provide good approximations to the support of probability distributions. In addition to reachability analysis, the same approach can be applied to general problems of estimating the support of a random variable, which has applications in data science towards detection of novelties and outliers in data sets. In applications where safety is a concern, having a guarantee of accuracy that holds on finite data sets is critical. In this paper, we prove such bounds for our algorithms under the Probably Approximately Correct (PAC) framework. In addition to applying classical Vapnik-Chervonenkis (VC) dimension bound arguments, we apply the PAC-Bayes theorem by leveraging a formal connection between kernelized empirical inverse Christoffel functions and Gaussian process regression models. The bound based on PAC-Bayes applies to a more general class of Christoffel functions than the VC dimension argument, and achieves greater sample efficiency in experiments.

Learning-based Initialization Strategy for Safety of Multi-Vehicle Systems

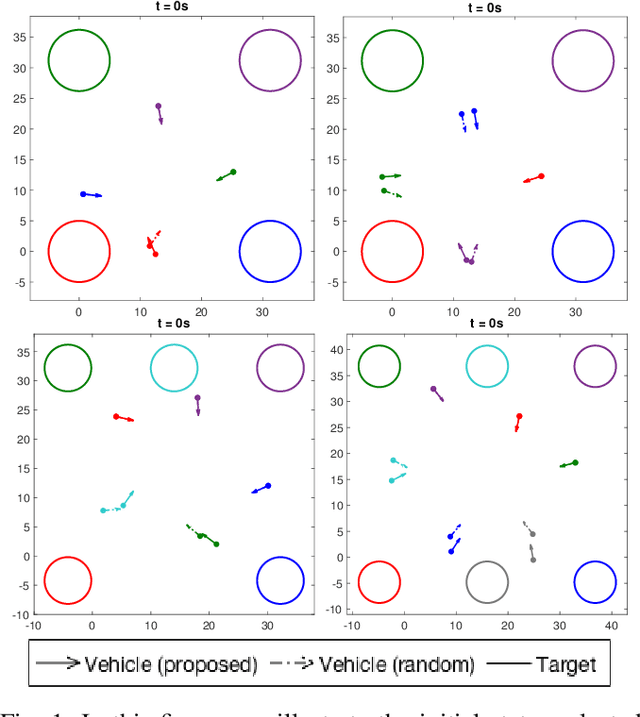
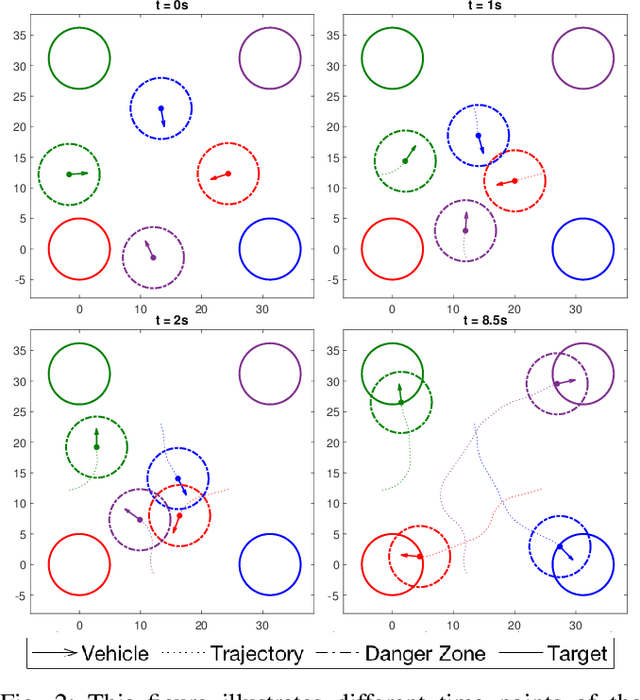
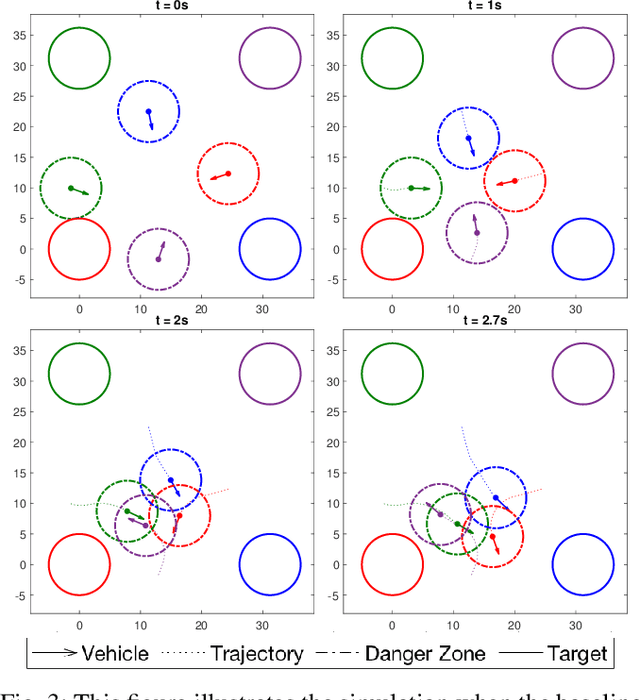
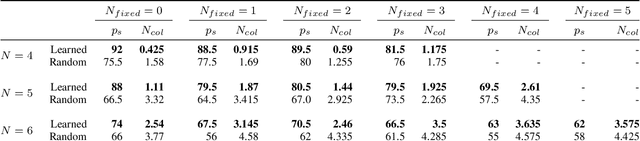
Multi-vehicle collision avoidance is a highly crucial problem due to the soaring interests of introducing autonomous vehicles into the real world in recent years. The safety of these vehicles while they complete their objectives is of paramount importance. Hamilton-Jacobi (HJ) reachability is a promising tool for guaranteeing safety for low-dimensional systems. However, due to its exponential complexity in computation time, no reachability-based methods have been able to guarantee safety for more than three vehicles successfully in unstructured scenarios. For systems with four or more vehicles,we can only empirically validate their safety performance.While reachability-based safety methods enjoy a flexible least-restrictive control strategy, it is challenging to reason about long-horizon trajectories online because safety at any given state is determined by looking up its safety value in a pre-computed table that does not exhibit favorable properties that continuous functions have. This motivates the problem of improving the safety performance of unstructured multi-vehicle systems when safety cannot be guaranteed given any least-restrictive safety-aware collision avoidance algorithm while avoiding online trajectory optimization. In this paper, we propose a novel approach using supervised learning to enhance the safety of vehicles by proposing new initial states in very close neighborhood of the original initial states of vehicles. Our experiments demonstrate the effectiveness of our proposed approach and show that vehicles are able to get to their goals with better safety performance with our approach compared to a baseline approach in wide-ranging scenarios.

Recurrent Neural Network Controllers Synthesis with Stability Guarantees for Partially Observed Systems

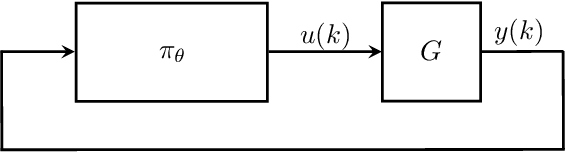
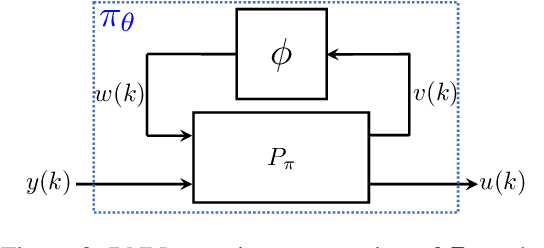
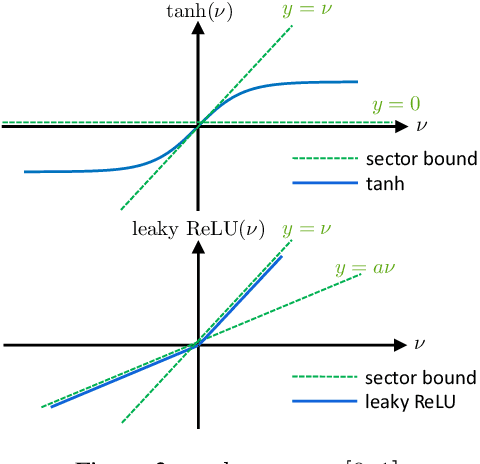
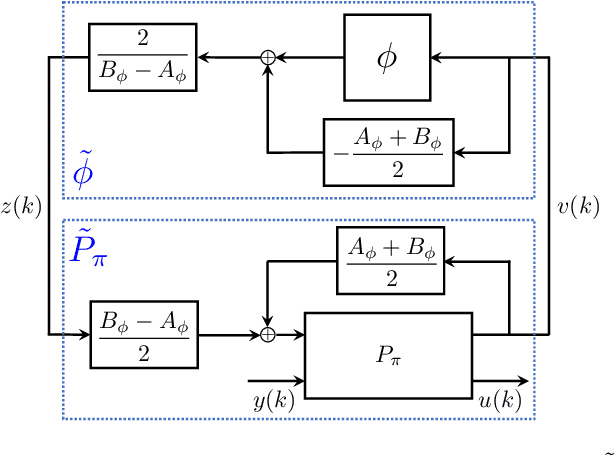
Neural network controllers have become popular in control tasks thanks to their flexibility and expressivity. Stability is a crucial property for safety-critical dynamical systems, while stabilization of partially observed systems, in many cases, requires controllers to retain and process long-term memories of the past. We consider the important class of recurrent neural networks (RNN) as dynamic controllers for nonlinear uncertain partially-observed systems, and derive convex stability conditions based on integral quadratic constraints, S-lemma and sequential convexification. To ensure stability during the learning and control process, we propose a projected policy gradient method that iteratively enforces the stability conditions in the reparametrized space taking advantage of mild additional information on system dynamics. Numerical experiments show that our method learns stabilizing controllers while using fewer samples and achieving higher final performance compared with policy gradient.

Reachability-based Safe Planning for Multi-Vehicle Systems withMultiple Targets

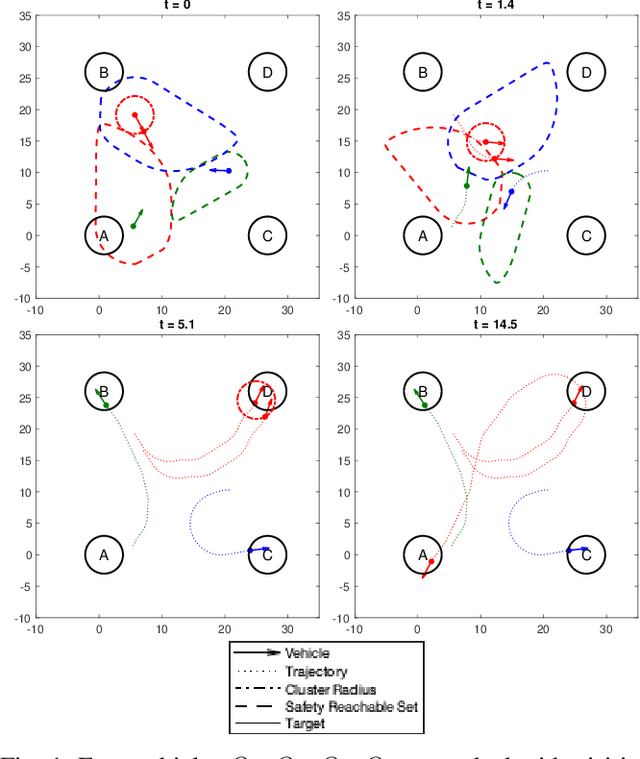
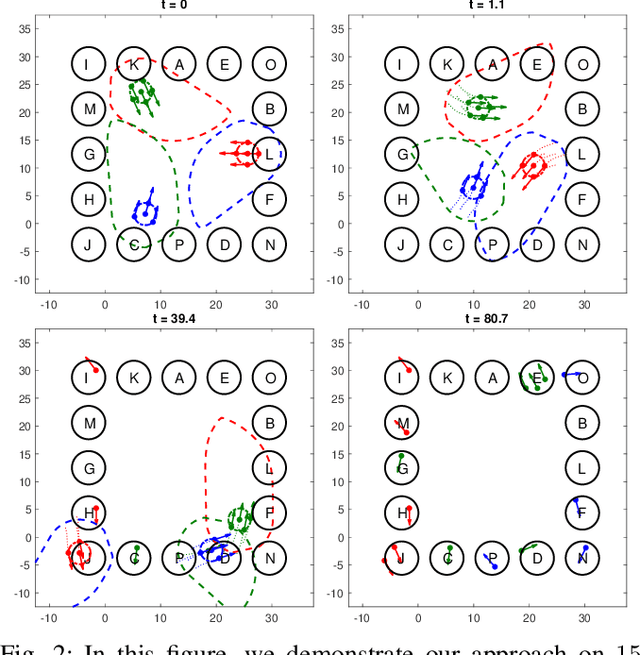
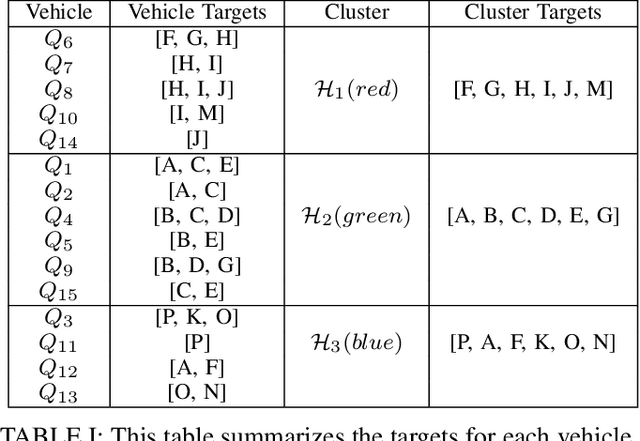
Recently there have been a lot of interests in introducing UAVs for a wide range of applications, making ensuring safety of multi-vehicle systems a highly crucial problem. Hamilton-Jacobi (HJ) reachability is a promising tool for analyzing safety of vehicles for low-dimensional systems. However, reachability suffers from the curse of dimensionality, making its direct application to more than two vehicles intractable. Recent works have made it tractable to guarantee safety for 3 and 4 vehicles with reachability. However, the number of vehicles safety can be guaranteed for remains small. In this paper, we propose a novel reachability-based approach that guarantees safety for any number of vehicles while vehicles complete their objectives of visiting multiple targets efficiently, given any K-vehicle collision avoidance algorithm where K can in general be a small number. We achieve this by developing an approach to group vehicles into clusters efficiently and a control strategy that guarantees safety for any in-cluster and cross-cluster pair of vehicles for all time. Our proposed method is scalable to large number of vehicles with little computation overhead. We demonstrate our proposed approach with a simulation on 15 vehicles. In addition, we contribute a more general solution to the 3-vehicle collision avoidance problem from a past recent work, show that the prior work is a special case of our proposed generalization, and prove its validity.

Text Analytics for Resilience-Enabled Extreme EventsReconnaissance

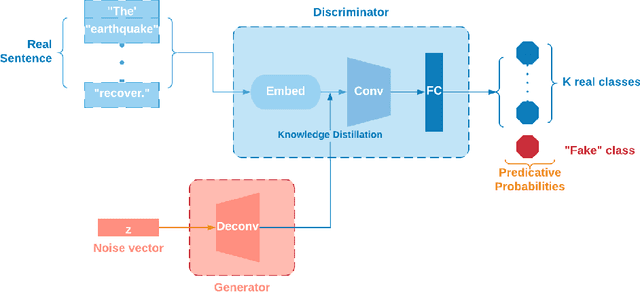
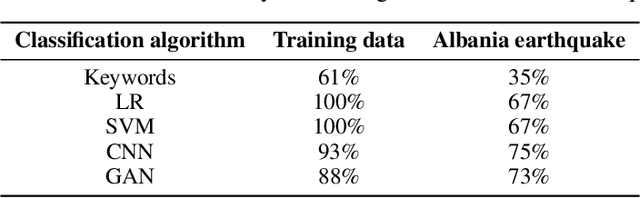
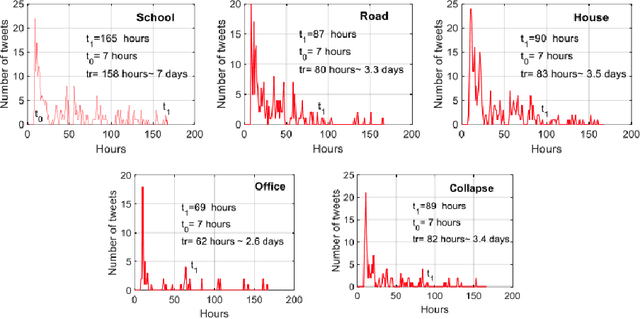
Post-hazard reconnaissance for natural disasters (e.g., earthquakes) is important for understanding the performance of the built environment, speeding up the recovery, enhancing resilience and making informed decisions related to current and future hazards. Natural language processing (NLP) is used in this study for the purposes of increasing the accuracy and efficiency of natural hazard reconnaissance through automation. The study particularly focuses on (1) automated data (news and social media) collection hosted by the Pacific Earthquake Engineering Research (PEER) Center server, (2) automatic generation of reconnaissance reports, and (3) use of social media to extract post-hazard information such as the recovery time. Obtained results are encouraging for further development and wider usage of various NLP methods in natural hazard reconnaissance.

Implicit Graph Neural Networks

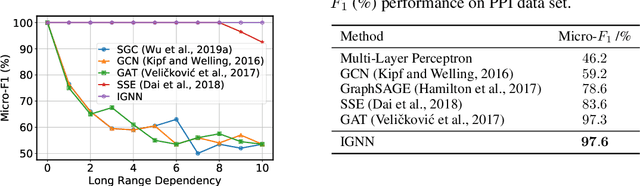
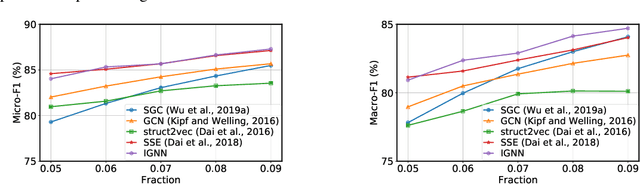
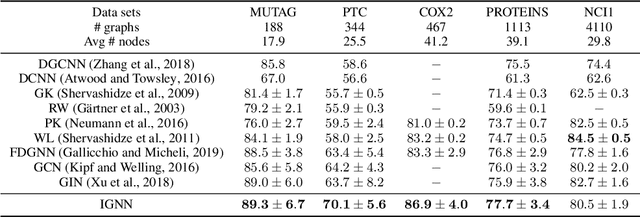
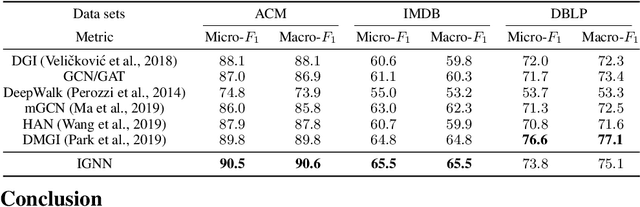
Graph Neural Networks (GNNs) are widely used deep learning models that learn meaningful representations from graph-structured data. Due to the finite nature of the underlying recurrent structure, current GNN methods may struggle to capture long-range dependencies in underlying graphs. To overcome this difficulty, we propose a graph learning framework, called Implicit Graph Neural Networks (IGNN), where predictions are based on the solution of a fixed-point equilibrium equation involving implicitly defined "state" vectors. We use the Perron-Frobenius theory to derive sufficient conditions that ensure well-posedness of the framework. Leveraging implicit differentiation, we derive a tractable projected gradient descent method to train the framework. Experiments on a comprehensive range of tasks show that IGNNs consistently capture long-range dependencies and outperform the state-of-the-art GNN models.

FANOK: Knockoffs in Linear Time

We describe a series of algorithms that efficiently implement Gaussian model-X knockoffs to control the false discovery rate on large scale feature selection problems. Identifying the knockoff distribution requires solving a large scale semidefinite program for which we derive several efficient methods. One handles generic covariance matrices, has a complexity scaling as $O(p^3)$ where $p$ is the ambient dimension, while another assumes a rank $k$ factor model on the covariance matrix to reduce this complexity bound to $O(pk^2)$. We also derive efficient procedures to both estimate factor models and sample knockoff covariates with complexity linear in the dimension. We test our methods on problems with $p$ as large as $500,000$.