FANOK: Knockoffs in Linear Time

We describe a series of algorithms that efficiently implement Gaussian model-X knockoffs to control the false discovery rate on large scale feature selection problems. Identifying the knockoff distribution requires solving a large scale semidefinite program for which we derive several efficient methods. One handles generic covariance matrices, has a complexity scaling as $O(p^3)$ where $p$ is the ambient dimension, while another assumes a rank $k$ factor model on the covariance matrix to reduce this complexity bound to $O(pk^2)$. We also derive efficient procedures to both estimate factor models and sample knockoff covariates with complexity linear in the dimension. We test our methods on problems with $p$ as large as $500,000$.

Implicit Deep Learning

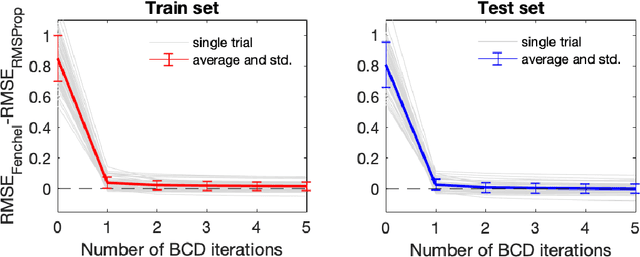
We define a new class of "implicit" deep learning prediction rules that generalize the recursive rules of feedforward neural networks. These models are based on the solution of a fixed-point equation involving a single a vector of hidden features, which is thus only implicitly defined. The new framework greatly simplifies the notation of deep learning, and opens up new possibilities, in terms of novel architectures and algorithms, robustness analysis and design, interpretability, sparsity, and network architecture optimization.

Naive Feature Selection: Sparsity in Naive Bayes

Due to its linear complexity, naive Bayes classification remains an attractive supervised learning method, especially in very large-scale settings. We propose a sparse version of naive Bayes, which can be used for feature selection. This leads to a combinatorial maximum-likelihood problem, for which we provide an exact solution in the case of binary data, or a bound in the multinomial case. We prove that our bound becomes tight as the marginal contribution of additional features decreases. Both binary and multinomial sparse models are solvable in time almost linear in problem size, representing a very small extra relative cost compared to the classical naive Bayes. Numerical experiments on text data show that the naive Bayes feature selection method is as statistically effective as state-of-the-art feature selection methods such as recursive feature elimination, $l_1$-penalized logistic regression and LASSO, while being orders of magnitude faster. For a large data set, having more than with $1.6$ million training points and about $12$ million features, and with a non-optimized CPU implementation, our sparse naive Bayes model can be trained in less than 15 seconds.

Fenchel Lifted Networks: A Lagrange Relaxation of Neural Network Training

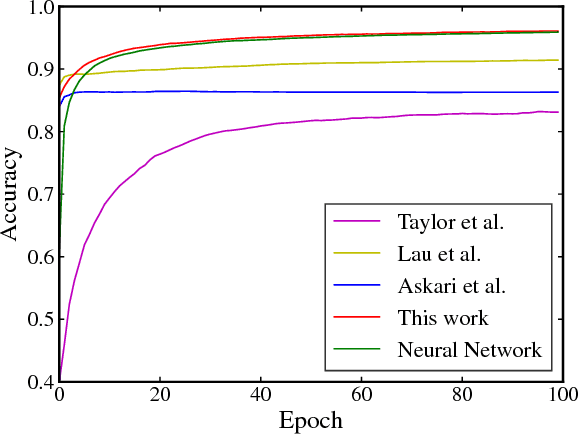
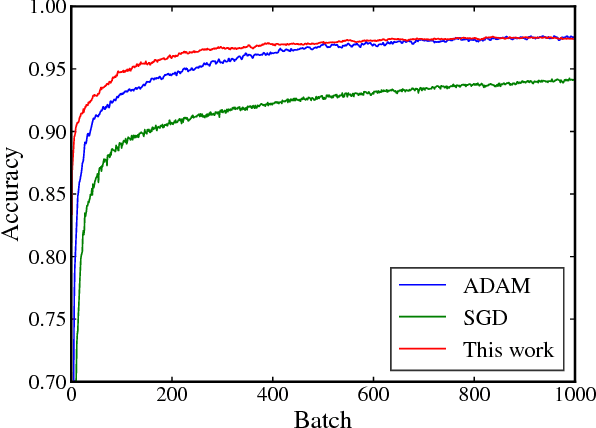
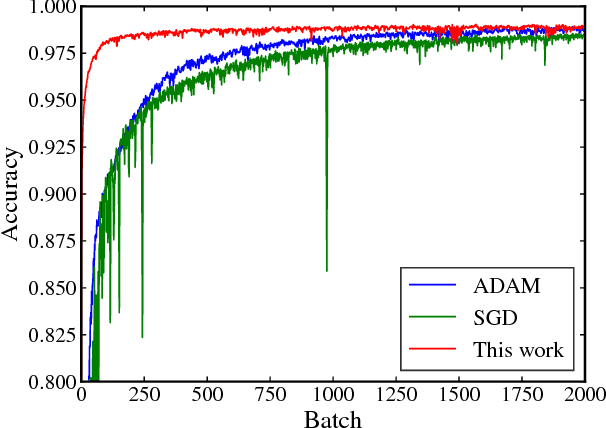
Despite the recent successes of deep neural networks, the corresponding training problem remains highly non-convex and difficult to optimize. Classes of models have been proposed that introduce greater structure to the objective function at the cost of lifting the dimension of the problem. However, these lifted methods sometimes perform poorly compared to traditional neural networks. In this paper, we introduce a new class of lifted models, Fenchel lifted networks, that enjoy the same benefits as previous lifted models, without suffering a degradation in performance over classical networks. Our model represents activation functions as equivalent biconvex constraints and uses Lagrange Multipliers to arrive at a rigorous lower bound of the traditional neural network training problem. This model is efficiently trained using block-coordinate descent and is parallelizable across data points and/or layers. We compare our model against standard fully connected and convolutional networks and show that we are able to match or beat their performance.

Frank-Wolfe Algorithm for Exemplar Selection

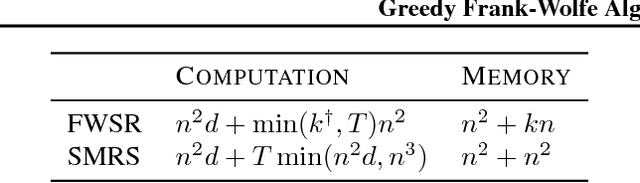
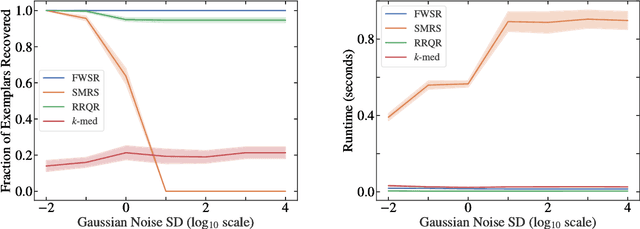
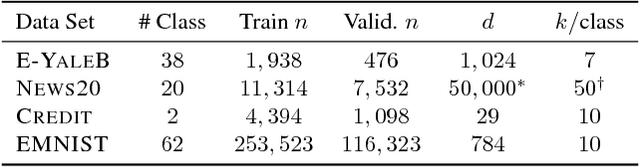
In this paper, we consider the problem of selecting representatives from a data set for arbitrary supervised/unsupervised learning tasks. We identify a subset $S$ of a data set $A$ such that 1) the size of $S$ is much smaller than $A$ and 2) $S$ efficiently describes the entire data set, in a way formalized via auto-regression. The set $S$, also known as the exemplars of the data set $A$, is constructed by solving a convex auto-regressive version of dictionary learning where the dictionary and measurements are given by the data matrix. We show that in order to generate $|S| = k$ exemplars, our algorithm, Frank-Wolfe Sparse Representation (FWSR), only requires $\approx k$ iterations with a per-iteration cost that is quadratic in the size of $A$, an order of magnitude faster than state of the art methods. We test our algorithm against current methods on 4 different data sets and are able to outperform other exemplar finding methods in almost all scenarios. We also test our algorithm qualitatively by selecting exemplars from a corpus of Donald Trump and Hillary Clinton's twitter posts.

Lifted Neural Networks

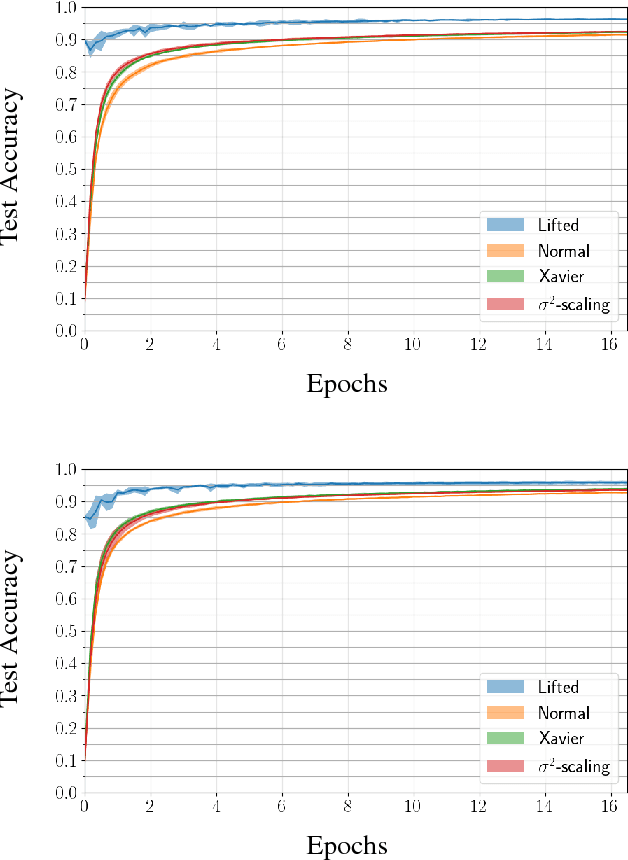
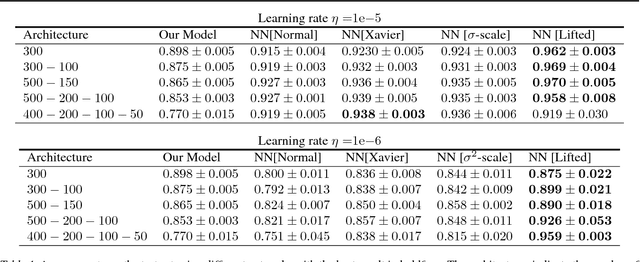
We describe a novel family of models of multi- layer feedforward neural networks in which the activation functions are encoded via penalties in the training problem. Our approach is based on representing a non-decreasing activation function as the argmin of an appropriate convex optimiza- tion problem. The new framework allows for algo- rithms such as block-coordinate descent methods to be applied, in which each step is composed of a simple (no hidden layer) supervised learning problem that is parallelizable across data points and/or layers. Experiments indicate that the pro- posed models provide excellent initial guesses for weights for standard neural networks. In addi- tion, the model provides avenues for interesting extensions, such as robustness against noisy in- puts and optimizing over parameters in activation functions.

Kernel-based Outlier Detection using the Inverse Christoffel Function

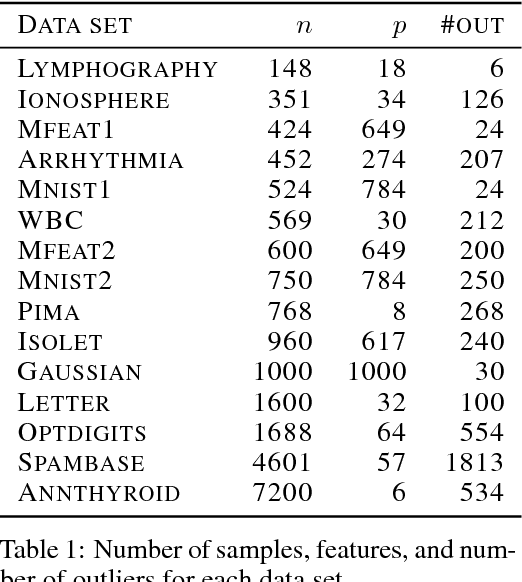
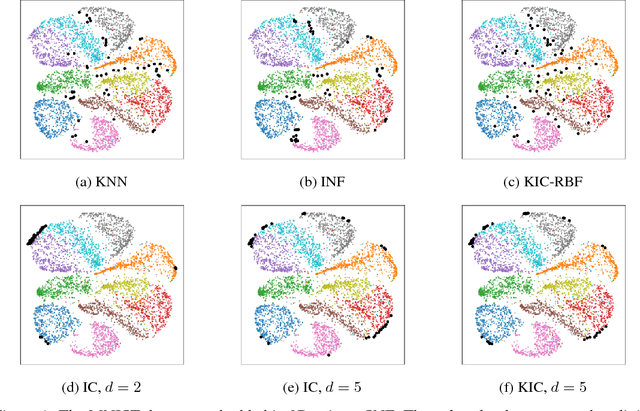
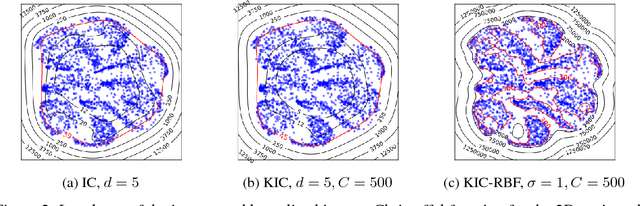
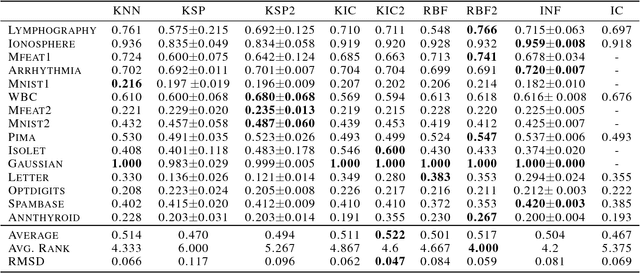
Outlier detection methods have become increasingly relevant in recent years due to increased security concerns and because of its vast application to different fields. Recently, Pauwels and Lasserre (2016) noticed that the sublevel sets of the inverse Christoffel function accurately depict the shape of a cloud of data using a sum-of-squares polynomial and can be used to perform outlier detection. In this work, we propose a kernelized variant of the inverse Christoffel function that makes it computationally tractable for data sets with a large number of features. We compare our approach to current methods on 15 different data sets and achieve the best average area under the precision recall curve (AUPRC) score, the best average rank and the lowest root mean square deviation.