Collaboratively Learning Linear Models with Structured Missing Data

We study the problem of collaboratively learning least squares estimates for $m$ agents. Each agent observes a different subset of the features$\unicode{x2013}$e.g., containing data collected from sensors of varying resolution. Our goal is to determine how to coordinate the agents in order to produce the best estimator for each agent. We propose a distributed, semi-supervised algorithm Collab, consisting of three steps: local training, aggregation, and distribution. Our procedure does not require communicating the labeled data, making it communication efficient and useful in settings where the labeled data is inaccessible. Despite this handicap, our procedure is nearly asymptotically local minimax optimal$\unicode{x2013}$even among estimators allowed to communicate the labeled data such as imputation methods. We test our method on real and synthetic data.

Causal Inference out of Control: Estimating the Steerability of Consumption

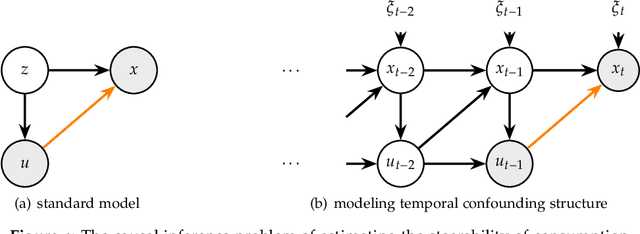
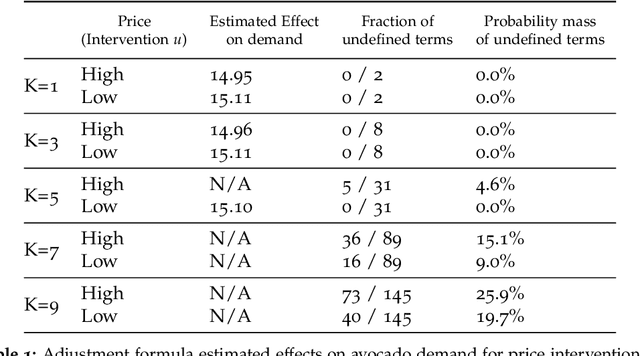
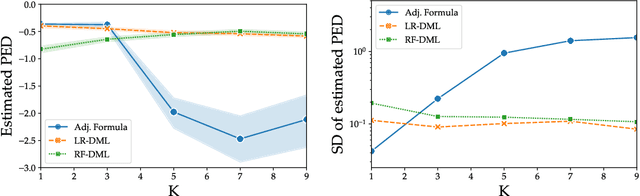
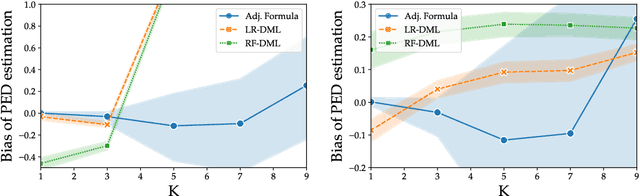
Regulators and academics are increasingly interested in the causal effect that algorithmic actions of a digital platform have on consumption. We introduce a general causal inference problem we call the steerability of consumption that abstracts many settings of interest. Focusing on observational designs and exploiting the structure of the problem, we exhibit a set of assumptions for causal identifiability that significantly weaken the often unrealistic overlap assumptions of standard designs. The key novelty of our approach is to explicitly model the dynamics of consumption over time, viewing the platform as a controller acting on a dynamical system. From this dynamical systems perspective, we are able to show that exogenous variation in consumption and appropriately responsive algorithmic control actions are sufficient for identifying steerability of consumption. Our results illustrate the fruitful interplay of control theory and causal inference, which we illustrate with examples from econometrics, macroeconomics, and machine learning.

Dual Multi-scale Mean Teacher Network for Semi-supervised Infection Segmentation in Chest CT Volume for COVID-19

Automated detecting lung infections from computed tomography (CT) data plays an important role for combating COVID-19. However, there are still some challenges for developing AI system. 1) Most current COVID-19 infection segmentation methods mainly relied on 2D CT images, which lack 3D sequential constraint. 2) Existing 3D CT segmentation methods focus on single-scale representations, which do not achieve the multiple level receptive field sizes on 3D volume. 3) The emergent breaking out of COVID-19 makes it hard to annotate sufficient CT volumes for training deep model. To address these issues, we first build a multiple dimensional-attention convolutional neural network (MDA-CNN) to aggregate multi-scale information along different dimension of input feature maps and impose supervision on multiple predictions from different CNN layers. Second, we assign this MDA-CNN as a basic network into a novel dual multi-scale mean teacher network (DM${^2}$T-Net) for semi-supervised COVID-19 lung infection segmentation on CT volumes by leveraging unlabeled data and exploring the multi-scale information. Our DM${^2}$T-Net encourages multiple predictions at different CNN layers from the student and teacher networks to be consistent for computing a multi-scale consistency loss on unlabeled data, which is then added to the supervised loss on the labeled data from multiple predictions of MDA-CNN. Third, we collect two COVID-19 segmentation datasets to evaluate our method. The experimental results show that our network consistently outperforms the compared state-of-the-art methods.

Private optimization in the interpolation regime: faster rates and hardness results

In non-private stochastic convex optimization, stochastic gradient methods converge much faster on interpolation problems -- problems where there exists a solution that simultaneously minimizes all of the sample losses -- than on non-interpolating ones; we show that generally similar improvements are impossible in the private setting. However, when the functions exhibit quadratic growth around the optimum, we show (near) exponential improvements in the private sample complexity. In particular, we propose an adaptive algorithm that improves the sample complexity to achieve expected error $\alpha$ from $\frac{d}{\varepsilon \sqrt{\alpha}}$ to $\frac{1}{\alpha^\rho} + \frac{d}{\varepsilon} \log\left(\frac{1}{\alpha}\right)$ for any fixed $\rho >0$, while retaining the standard minimax-optimal sample complexity for non-interpolation problems. We prove a lower bound that shows the dimension-dependent term is tight. Furthermore, we provide a superefficiency result which demonstrates the necessity of the polynomial term for adaptive algorithms: any algorithm that has a polylogarithmic sample complexity for interpolation problems cannot achieve the minimax-optimal rates for the family of non-interpolation problems.

PV-RCNN++: Semantical Point-Voxel Feature Interaction for 3D Object Detection

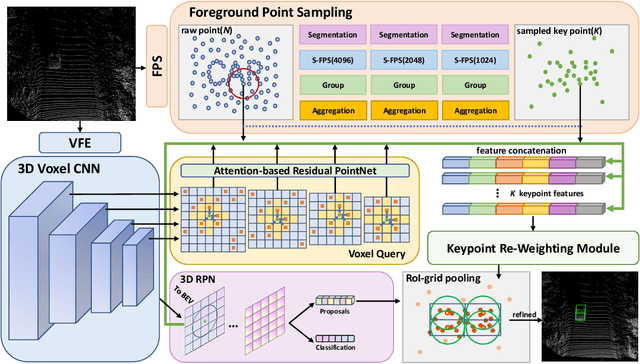
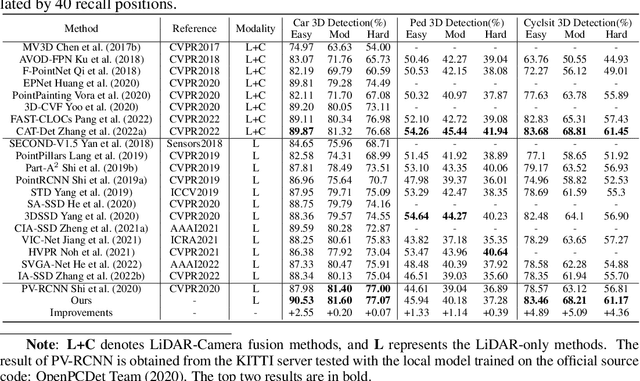
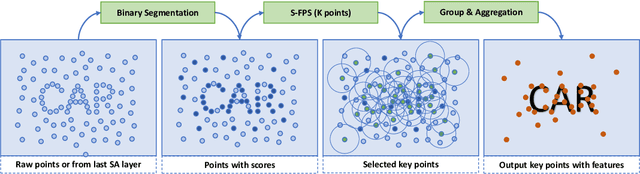
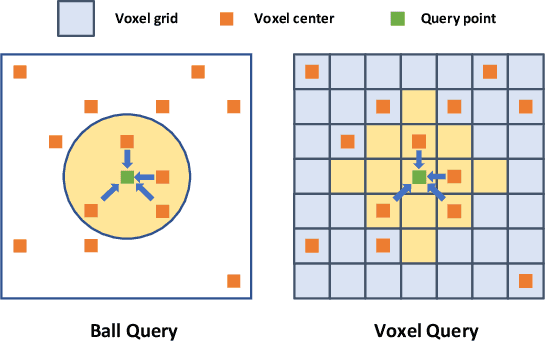
Large imbalance often exists between the foreground points (i.e., objects) and the background points in outdoor LiDAR point clouds. It hinders cutting-edge detectors from focusing on informative areas to produce accurate 3D object detection results. This paper proposes a novel object detection network by semantical point-voxel feature interaction, dubbed PV-RCNN++. Unlike most of existing methods, PV-RCNN++ explores the semantic information to enhance the quality of object detection. First, a semantic segmentation module is proposed to retain more discriminative foreground keypoints. Such a module will guide our PV-RCNN++ to integrate more object-related point-wise and voxel-wise features in the pivotal areas. Then, to make points and voxels interact efficiently, we utilize voxel query based on Manhattan distance to quickly sample voxel-wise features around keypoints. Such the voxel query will reduce the time complexity from O(N) to O(K), compared to the ball query. Further, to avoid being stuck in learning only local features, an attention-based residual PointNet module is designed to expand the receptive field to adaptively aggregate the neighboring voxel-wise features into keypoints. Extensive experiments on the KITTI dataset show that PV-RCNN++ achieves 81.60$\%$, 40.18$\%$, 68.21$\%$ 3D mAP on Car, Pedestrian, and Cyclist, achieving comparable or even better performance to the state-of-the-arts.

Semi-MoreGAN: A New Semi-supervised Generative Adversarial Network for Mixture of Rain Removal

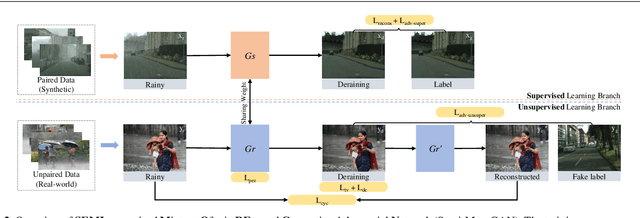
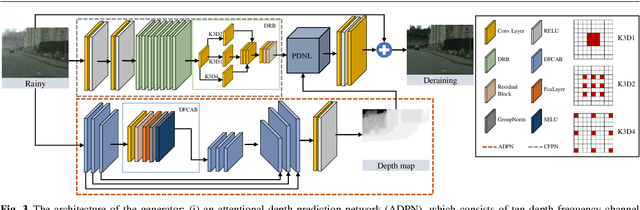
Rain is one of the most common weather which can completely degrade the image quality and interfere with the performance of many computer vision tasks, especially under heavy rain conditions. We observe that: (i) rain is a mixture of rain streaks and rainy haze; (ii) the scene depth determines the intensity of rain streaks and the transformation into the rainy haze; (iii) most existing deraining methods are only trained on synthetic rainy images, and hence generalize poorly to the real-world scenes. Motivated by these observations, we propose a new SEMI-supervised Mixture Of rain REmoval Generative Adversarial Network (Semi-MoreGAN), which consists of four key modules: (I) a novel attentional depth prediction network to provide precise depth estimation; (ii) a context feature prediction network composed of several well-designed detailed residual blocks to produce detailed image context features; (iii) a pyramid depth-guided non-local network to effectively integrate the image context with the depth information, and produce the final rain-free images; and (iv) a comprehensive semi-supervised loss function to make the model not limited to synthetic datasets but generalize smoothly to real-world heavy rainy scenes. Extensive experiments show clear improvements of our approach over twenty representative state-of-the-arts on both synthetic and real-world rainy images.

Approximate Function Evaluation via Multi-Armed Bandits

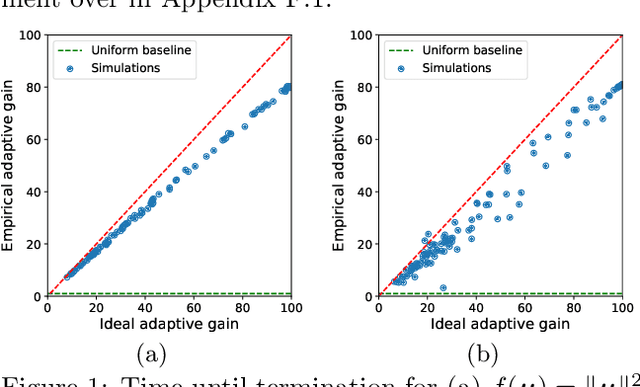
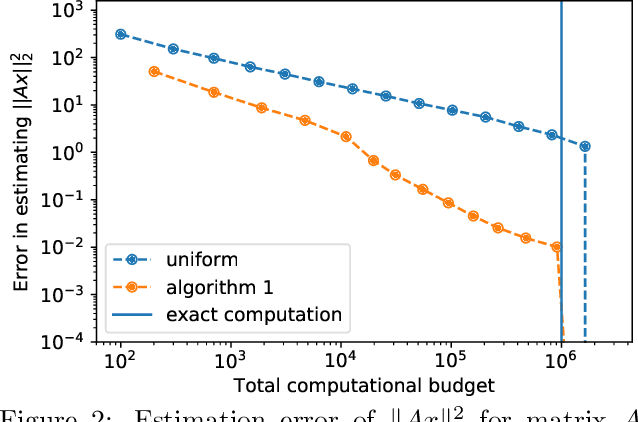
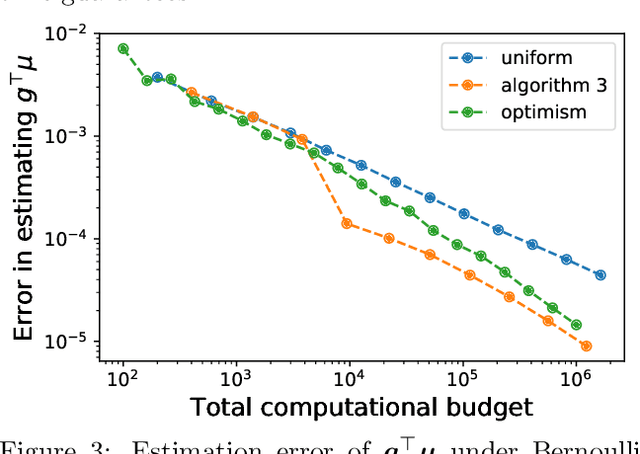
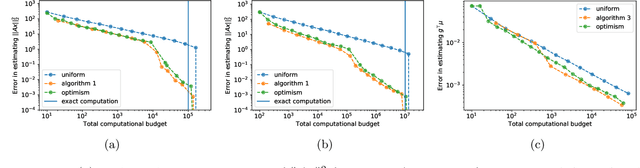
We study the problem of estimating the value of a known smooth function $f$ at an unknown point $\boldsymbol{\mu} \in \mathbb{R}^n$, where each component $\mu_i$ can be sampled via a noisy oracle. Sampling more frequently components of $\boldsymbol{\mu}$ corresponding to directions of the function with larger directional derivatives is more sample-efficient. However, as $\boldsymbol{\mu}$ is unknown, the optimal sampling frequencies are also unknown. We design an instance-adaptive algorithm that learns to sample according to the importance of each coordinate, and with probability at least $1-\delta$ returns an $\epsilon$ accurate estimate of $f(\boldsymbol{\mu})$. We generalize our algorithm to adapt to heteroskedastic noise, and prove asymptotic optimality when $f$ is linear. We corroborate our theoretical results with numerical experiments, showing the dramatic gains afforded by adaptivity.

When A Conventional Filter Meets Deep Learning: Basis Composition Learning on Image Filters

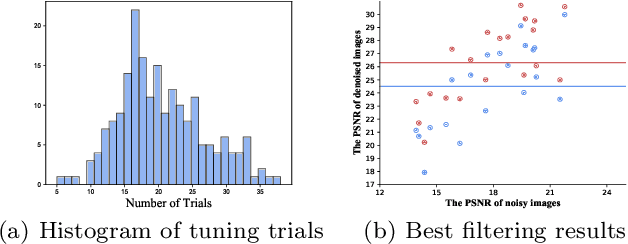
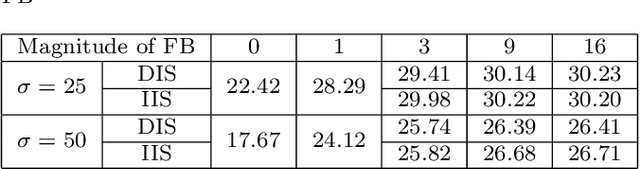
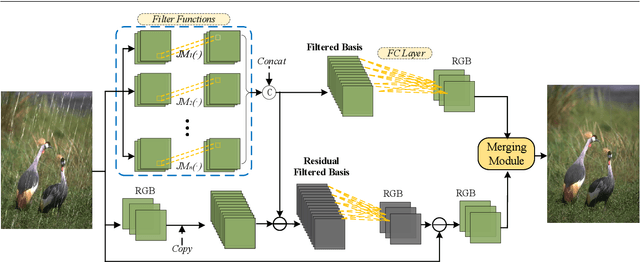
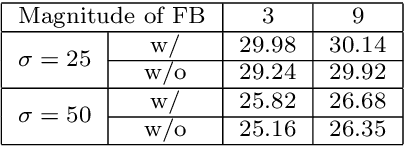
Image filters are fast, lightweight and effective, which make these conventional wisdoms preferable as basic tools in vision tasks. In practical scenarios, users have to tweak parameters multiple times to obtain satisfied results. This inconvenience heavily discounts the efficiency and user experience. We propose basis composition learning on single image filters to automatically determine their optimal formulas. The feasibility is based on a two-step strategy: first, we build a set of filtered basis (FB) consisting of approximations under selected parameter configurations; second, a dual-branch composition module is proposed to learn how the candidates in FB are combined to better approximate the target image. Our method is simple yet effective in practice; it renders filters to be user-friendly and benefits fundamental low-level vision problems including denoising, deraining and texture removal. Extensive experiments demonstrate that our method achieves an appropriate balance among the performance, time complexity and memory efficiency.

Fine-tuning is Fine in Federated Learning

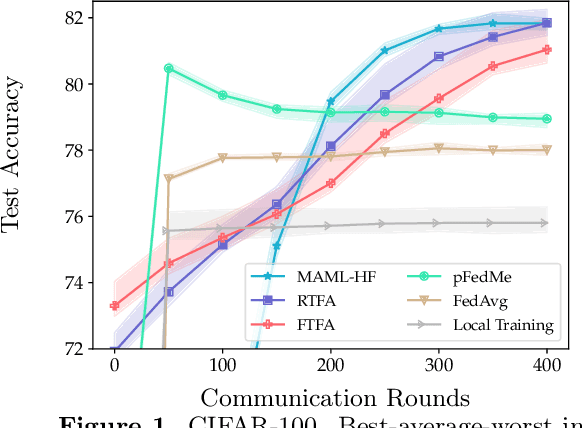
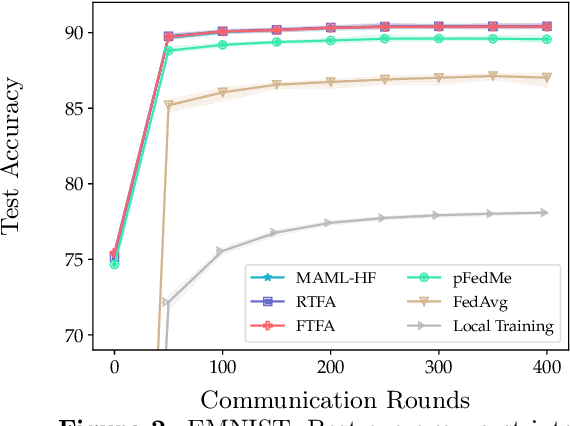
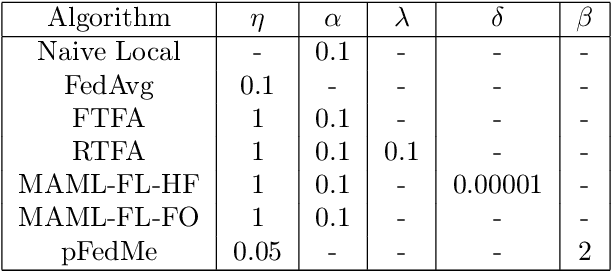
We study the performance of federated learning algorithms and their variants in an asymptotic framework. Our starting point is the formulation of federated learning as a multi-criterion objective, where the goal is to minimize each client's loss using information from all of the clients. We propose a linear regression model, where, for a given client, we theoretically compare the performance of various algorithms in the high-dimensional asymptotic limit. This asymptotic multi-criterion approach naturally models the high-dimensional, many-device nature of federated learning and suggests that personalization is central to federated learning. Our theory suggests that Fine-tuned Federated Averaging (FTFA), i.e., Federated Averaging followed by local training, and the ridge regularized variant Ridge-tuned Federated Averaging (RTFA) are competitive with more sophisticated meta-learning and proximal-regularized approaches. In addition to being conceptually simpler, FTFA and RTFA are computationally more efficient than its competitors. We corroborate our theoretical claims with extensive experiments on federated versions of the EMNIST, CIFAR-100, Shakespeare, and Stack Overflow datasets.

Accelerated, Optimal, and Parallel: Some Results on Model-Based Stochastic Optimization

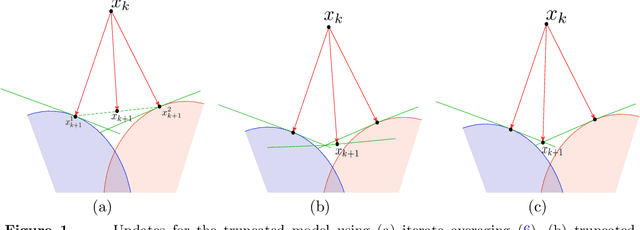
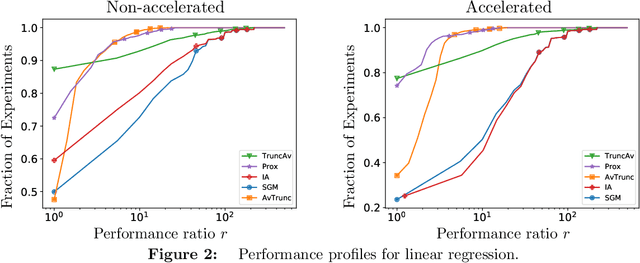
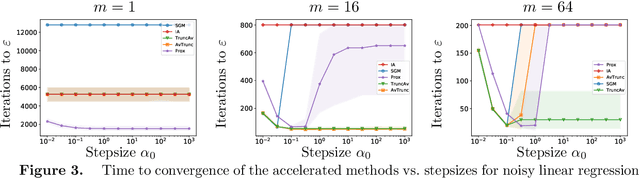
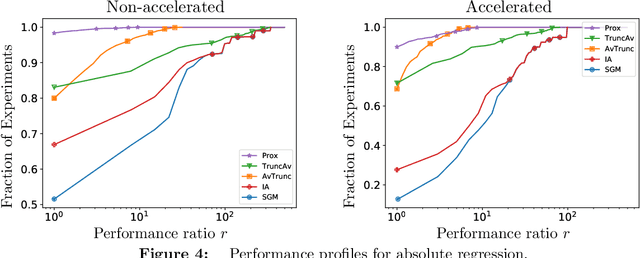
We extend the Approximate-Proximal Point (aProx) family of model-based methods for solving stochastic convex optimization problems, including stochastic subgradient, proximal point, and bundle methods, to the minibatch and accelerated setting. To do so, we propose specific model-based algorithms and an acceleration scheme for which we provide non-asymptotic convergence guarantees, which are order-optimal in all problem-dependent constants and provide linear speedup in minibatch size, while maintaining the desirable robustness traits (e.g. to stepsize) of the aProx family. Additionally, we show improved convergence rates and matching lower bounds identifying new fundamental constants for "interpolation" problems, whose importance in statistical machine learning is growing; this, for example, gives a parallelization strategy for alternating projections. We corroborate our theoretical results with empirical testing to demonstrate the gains accurate modeling, acceleration, and minibatching provide.