Fine-tuning is Fine in Federated Learning
Paper and Code
Aug 16, 2021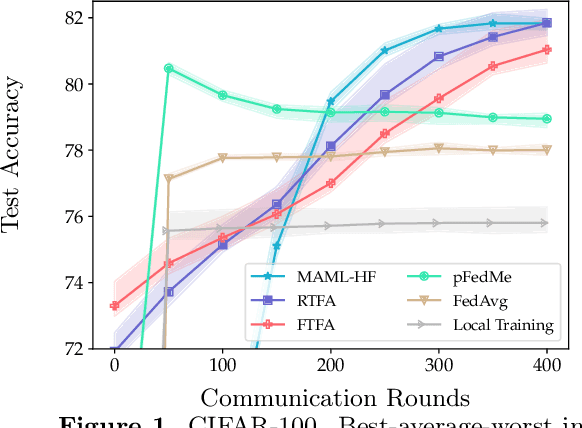

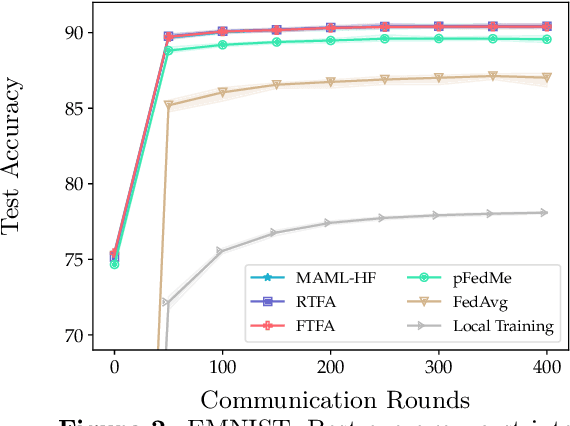
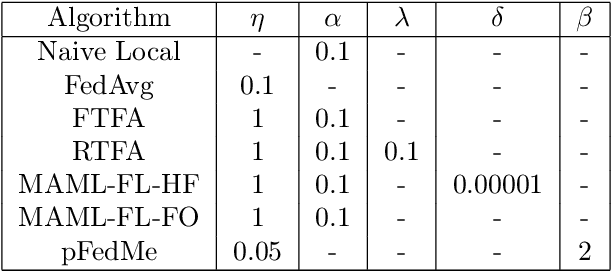
We study the performance of federated learning algorithms and their variants in an asymptotic framework. Our starting point is the formulation of federated learning as a multi-criterion objective, where the goal is to minimize each client's loss using information from all of the clients. We propose a linear regression model, where, for a given client, we theoretically compare the performance of various algorithms in the high-dimensional asymptotic limit. This asymptotic multi-criterion approach naturally models the high-dimensional, many-device nature of federated learning and suggests that personalization is central to federated learning. Our theory suggests that Fine-tuned Federated Averaging (FTFA), i.e., Federated Averaging followed by local training, and the ridge regularized variant Ridge-tuned Federated Averaging (RTFA) are competitive with more sophisticated meta-learning and proximal-regularized approaches. In addition to being conceptually simpler, FTFA and RTFA are computationally more efficient than its competitors. We corroborate our theoretical claims with extensive experiments on federated versions of the EMNIST, CIFAR-100, Shakespeare, and Stack Overflow datasets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge