Faster Rates for Private Adversarial Bandits

We design new differentially private algorithms for the problems of adversarial bandits and bandits with expert advice. For adversarial bandits, we give a simple and efficient conversion of any non-private bandit algorithm to a private bandit algorithm. Instantiating our conversion with existing non-private bandit algorithms gives a regret upper bound of $O\left(\frac{\sqrt{KT}}{\sqrt{\epsilon}}\right)$, improving upon the existing upper bound $O\left(\frac{\sqrt{KT \log(KT)}}{\epsilon}\right)$ for all $\epsilon \leq 1$. In particular, our algorithms allow for sublinear expected regret even when $\epsilon \leq \frac{1}{\sqrt{T}}$, establishing the first known separation between central and local differential privacy for this problem. For bandits with expert advice, we give the first differentially private algorithms, with expected regret $O\left(\frac{\sqrt{NT}}{\sqrt{\epsilon}}\right), O\left(\frac{\sqrt{KT\log(N)}\log(KT)}{\epsilon}\right)$, and $\tilde{O}\left(\frac{N^{1/6}K^{1/2}T^{2/3}\log(NT)}{\epsilon ^{1/3}} + \frac{N^{1/2}\log(NT)}{\epsilon}\right)$, where $K$ and $N$ are the number of actions and experts respectively. These rates allow us to get sublinear regret for different combinations of small and large $K, N$ and $\epsilon.$

ABoN: Adaptive Best-of-N Alignment

Recent advances in test-time alignment methods, such as Best-of-N sampling, offer a simple and effective way to steer language models (LMs) toward preferred behaviors using reward models (RM). However, these approaches can be computationally expensive, especially when applied uniformly across prompts without accounting for differences in alignment difficulty. In this work, we propose a prompt-adaptive strategy for Best-of-N alignment that allocates inference-time compute more efficiently. Motivated by latency concerns, we develop a two-stage algorithm: an initial exploratory phase estimates the reward distribution for each prompt using a small exploration budget, and a second stage adaptively allocates the remaining budget using these estimates. Our method is simple, practical, and compatible with any LM/RM combination. Empirical results on the AlpacaEval dataset for 12 LM/RM pairs and 50 different batches of prompts show that our adaptive strategy consistently outperforms the uniform allocation with the same inference budget. Moreover, our experiments show that our adaptive strategy remains competitive against uniform allocations with 20% larger inference budgets and even improves in performance as the batch size grows.

On Privately Estimating a Single Parameter

We investigate differentially private estimators for individual parameters within larger parametric models. While generic private estimators exist, the estimators we provide repose on new local notions of estimand stability, and these notions allow procedures that provide private certificates of their own stability. By leveraging these private certificates, we provide computationally and statistical efficient mechanisms that release private statistics that are, at least asymptotically in the sample size, essentially unimprovable: they achieve instance optimal bounds. Additionally, we investigate the practicality of the algorithms both in simulated data and in real-world data from the American Community Survey and US Census, highlighting scenarios in which the new procedures are successful and identifying areas for future work.

PREAMBLE: Private and Efficient Aggregation of Block Sparse Vectors and Applications

We revisit the problem of secure aggregation of high-dimensional vectors in a two-server system such as Prio. These systems are typically used to aggregate vectors such as gradients in private federated learning, where the aggregate itself is protected via noise addition to ensure differential privacy. Existing approaches require communication scaling with the dimensionality, and thus limit the dimensionality of vectors one can efficiently process in this setup. We propose PREAMBLE: Private Efficient Aggregation Mechanism for BLock-sparse Euclidean Vectors. PREAMBLE is a novel extension of distributed point functions that enables communication- and computation-efficient aggregation of block-sparse vectors, which are sparse vectors where the non-zero entries occur in a small number of clusters of consecutive coordinates. We then show that PREAMBLE can be combined with random sampling and privacy amplification by sampling results, to allow asymptotically optimal privacy-utility trade-offs for vector aggregation, at a fraction of the communication cost. When coupled with recent advances in numerical privacy accounting, our approach incurs a negligible overhead in noise variance, compared to the Gaussian mechanism used with Prio.

Tracking the Best Expert Privately

We design differentially private algorithms for the problem of prediction with expert advice under dynamic regret, also known as tracking the best expert. Our work addresses three natural types of adversaries, stochastic with shifting distributions, oblivious, and adaptive, and designs algorithms with sub-linear regret for all three cases. In particular, under a shifting stochastic adversary where the distribution may shift $S$ times, we provide an $\epsilon$-differentially private algorithm whose expected dynamic regret is at most $O\left( \sqrt{S T \log (NT)} + \frac{S \log (NT)}{\epsilon}\right)$, where $T$ and $N$ are the epsilon horizon and number of experts, respectively. For oblivious adversaries, we give a reduction from dynamic regret minimization to static regret minimization, resulting in an upper bound of $O\left(\sqrt{S T \log(NT)} + \frac{S T^{1/3}\log(T/\delta) \log(NT)}{\epsilon^{2/3}}\right)$ on the expected dynamic regret, where $S$ now denotes the allowable number of switches of the best expert. Finally, similar to static regret, we establish a fundamental separation between oblivious and adaptive adversaries for the dynamic setting: while our algorithms show that sub-linear regret is achievable for oblivious adversaries in the high-privacy regime $\epsilon \le \sqrt{S/T}$, we show that any $(\epsilon, \delta)$-differentially private algorithm must suffer linear dynamic regret under adaptive adversaries for $\epsilon \le \sqrt{S/T}$. Finally, to complement this lower bound, we give an $\epsilon$-differentially private algorithm that attains sub-linear dynamic regret under adaptive adversaries whenever $\epsilon \gg \sqrt{S/T}$.

Faster Algorithms for User-Level Private Stochastic Convex Optimization

We study private stochastic convex optimization (SCO) under user-level differential privacy (DP) constraints. In this setting, there are $n$ users (e.g., cell phones), each possessing $m$ data items (e.g., text messages), and we need to protect the privacy of each user's entire collection of data items. Existing algorithms for user-level DP SCO are impractical in many large-scale machine learning scenarios because: (i) they make restrictive assumptions on the smoothness parameter of the loss function and require the number of users to grow polynomially with the dimension of the parameter space; or (ii) they are prohibitively slow, requiring at least $(mn)^{3/2}$ gradient computations for smooth losses and $(mn)^3$ computations for non-smooth losses. To address these limitations, we provide novel user-level DP algorithms with state-of-the-art excess risk and runtime guarantees, without stringent assumptions. First, we develop a linear-time algorithm with state-of-the-art excess risk (for a non-trivial linear-time algorithm) under a mild smoothness assumption. Our second algorithm applies to arbitrary smooth losses and achieves optimal excess risk in $\approx (mn)^{9/8}$ gradient computations. Third, for non-smooth loss functions, we obtain optimal excess risk in $n^{11/8} m^{5/4}$ gradient computations. Moreover, our algorithms do not require the number of users to grow polynomially with the dimension.

Private Online Learning via Lazy Algorithms

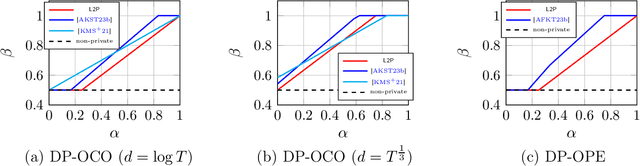
We study the problem of private online learning, specifically, online prediction from experts (OPE) and online convex optimization (OCO). We propose a new transformation that transforms lazy online learning algorithms into private algorithms. We apply our transformation for differentially private OPE and OCO using existing lazy algorithms for these problems. Our final algorithms obtain regret, which significantly improves the regret in the high privacy regime $\varepsilon \ll 1$, obtaining $\sqrt{T \log d} + T^{1/3} \log(d)/\varepsilon^{2/3}$ for DP-OPE and $\sqrt{T} + T^{1/3} \sqrt{d}/\varepsilon^{2/3}$ for DP-OCO. We also complement our results with a lower bound for DP-OPE, showing that these rates are optimal for a natural family of low-switching private algorithms.

Private Vector Mean Estimation in the Shuffle Model: Optimal Rates Require Many Messages

We study the problem of private vector mean estimation in the shuffle model of privacy where $n$ users each have a unit vector $v^{(i)} \in\mathbb{R}^d$. We propose a new multi-message protocol that achieves the optimal error using $\tilde{\mathcal{O}}\left(\min(n\varepsilon^2,d)\right)$ messages per user. Moreover, we show that any (unbiased) protocol that achieves optimal error requires each user to send $\Omega(\min(n\varepsilon^2,d)/\log(n))$ messages, demonstrating the optimality of our message complexity up to logarithmic factors. Additionally, we study the single-message setting and design a protocol that achieves mean squared error $\mathcal{O}(dn^{d/(d+2)}\varepsilon^{-4/(d+2)})$. Moreover, we show that any single-message protocol must incur mean squared error $\Omega(dn^{d/(d+2)})$, showing that our protocol is optimal in the standard setting where $\varepsilon = \Theta(1)$. Finally, we study robustness to malicious users and show that malicious users can incur large additive error with a single shuffler.

DP-Dueling: Learning from Preference Feedback without Compromising User Privacy

We consider the well-studied dueling bandit problem, where a learner aims to identify near-optimal actions using pairwise comparisons, under the constraint of differential privacy. We consider a general class of utility-based preference matrices for large (potentially unbounded) decision spaces and give the first differentially private dueling bandit algorithm for active learning with user preferences. Our proposed algorithms are computationally efficient with near-optimal performance, both in terms of the private and non-private regret bound. More precisely, we show that when the decision space is of finite size $K$, our proposed algorithm yields order optimal $O\Big(\sum_{i = 2}^K\log\frac{KT}{\Delta_i} + \frac{K}{\epsilon}\Big)$ regret bound for pure $\epsilon$-DP, where $\Delta_i$ denotes the suboptimality gap of the $i$-th arm. We also present a matching lower bound analysis which proves the optimality of our algorithms. Finally, we extend our results to any general decision space in $d$-dimensions with potentially infinite arms and design an $\epsilon$-DP algorithm with regret $\tilde{O} \left( \frac{d^6}{\kappa \epsilon } + \frac{ d\sqrt{T }}{\kappa} \right)$, providing privacy for free when $T \gg d$.

User-level Differentially Private Stochastic Convex Optimization: Efficient Algorithms with Optimal Rates

We study differentially private stochastic convex optimization (DP-SCO) under user-level privacy, where each user may hold multiple data items. Existing work for user-level DP-SCO either requires super-polynomial runtime [Ghazi et al. (2023)] or requires the number of users to grow polynomially with the dimensionality of the problem with additional strict assumptions [Bassily et al. (2023)]. We develop new algorithms for user-level DP-SCO that obtain optimal rates for both convex and strongly convex functions in polynomial time and require the number of users to grow only logarithmically in the dimension. Moreover, our algorithms are the first to obtain optimal rates for non-smooth functions in polynomial time. These algorithms are based on multiple-pass DP-SGD, combined with a novel private mean estimation procedure for concentrated data, which applies an outlier removal step before estimating the mean of the gradients.