Accelerating Scientific Research with Gemini: Case Studies and Common Techniques

Recent advances in large language models (LLMs) have opened new avenues for accelerating scientific research. While models are increasingly capable of assisting with routine tasks, their ability to contribute to novel, expert-level mathematical discovery is less understood. We present a collection of case studies demonstrating how researchers have successfully collaborated with advanced AI models, specifically Google's Gemini-based models (in particular Gemini Deep Think and its advanced variants), to solve open problems, refute conjectures, and generate new proofs across diverse areas in theoretical computer science, as well as other areas such as economics, optimization, and physics. Based on these experiences, we extract common techniques for effective human-AI collaboration in theoretical research, such as iterative refinement, problem decomposition, and cross-disciplinary knowledge transfer. While the majority of our results stem from this interactive, conversational methodology, we also highlight specific instances that push beyond standard chat interfaces. These include deploying the model as a rigorous adversarial reviewer to detect subtle flaws in existing proofs, and embedding it within a "neuro-symbolic" loop that autonomously writes and executes code to verify complex derivations. Together, these examples highlight the potential of AI not just as a tool for automation, but as a versatile, genuine partner in the creative process of scientific discovery.

Online Learning with Limited Information in the Sliding Window Model

Motivated by recent work on the experts problem in the streaming model, we consider the experts problem in the sliding window model. The sliding window model is a well-studied model that captures applications such as traffic monitoring, epidemic tracking, and automated trading, where recent information is more valuable than older data. Formally, we have $n$ experts, $T$ days, the ability to query the predictions of $q$ experts on each day, a limited amount of memory, and should achieve the (near-)optimal regret $\sqrt{nW}\text{polylog}(nT)$ regret over any window of the last $W$ days. While it is impossible to achieve such regret with $1$ query, we show that with $2$ queries we can achieve such regret and with only $\text{polylog}(nT)$ bits of memory. Not only are our algorithms optimal for sliding windows, but we also show for every interval $\mathcal{I}$ of days that we achieve $\sqrt{n|\mathcal{I}|}\text{polylog}(nT)$ regret with $2$ queries and only $\text{polylog}(nT)$ bits of memory, providing an exponential improvement on the memory of previous interval regret algorithms. Building upon these techniques, we address the bandit problem in data streams, where $q=1$, achieving $n T^{2/3}\text{polylog}(T)$ regret with $\text{polylog}(nT)$ memory, which is the first sublinear regret in the streaming model in the bandit setting with polylogarithmic memory; this can be further improved to the optimal $\mathcal{O}(\sqrt{nT})$ regret if the best expert's losses are in a random order.

Learning-Augmented Hierarchical Clustering

Hierarchical clustering (HC) is an important data analysis technique in which the goal is to recursively partition a dataset into a tree-like structure while grouping together similar data points at each level of granularity. Unfortunately, for many of the proposed HC objectives, there exist strong barriers to approximation algorithms with the hardness of approximation. Thus, we consider the problem of hierarchical clustering given auxiliary information from natural oracles. Specifically, we focus on a *splitting oracle* which, when provided with a triplet of vertices $(u,v,w)$, answers (possibly erroneously) the pairs of vertices whose lowest common ancestor includes all three vertices in an optimal tree, i.e., identifying which vertex ``splits away'' from the others. Using such an oracle, we obtain the following results: - A polynomial-time algorithm that outputs a hierarchical clustering tree with $O(1)$-approximation to the Dasgupta objective (Dasgupta [STOC'16]). - A near-linear time algorithm that outputs a hierarchical clustering tree with $(1-o(1))$-approximation to the Moseley-Wang objective (Moseley and Wang [NeurIPS'17]). Under the plausible Small Set Expansion Hypothesis, no polynomial-time algorithm can achieve any constant approximation for Dasgupta's objective or $(1-C)$-approximation for the Moseley-Wang objective for some constant $C>0$. As such, our results demonstrate that the splitting oracle enables algorithms to outperform standard HC approaches and overcome hardness constraints. Furthermore, our approaches extend to sublinear settings, in which we show new streaming and PRAM algorithms for HC with improved guarantees.

On the Price of Differential Privacy for Hierarchical Clustering

Hierarchical clustering is a fundamental unsupervised machine learning task with the aim of organizing data into a hierarchy of clusters. Many applications of hierarchical clustering involve sensitive user information, therefore motivating recent studies on differentially private hierarchical clustering under the rigorous framework of Dasgupta's objective. However, it has been shown that any privacy-preserving algorithm under edge-level differential privacy necessarily suffers a large error. To capture practical applications of this problem, we focus on the weight privacy model, where each edge of the input graph is at least unit weight. We present a novel algorithm in the weight privacy model that shows significantly better approximation than known impossibility results in the edge-level DP setting. In particular, our algorithm achieves $O(\log^{1.5}n/\varepsilon)$ multiplicative error for $\varepsilon$-DP and runs in polynomial time, where $n$ is the size of the input graph, and the cost is never worse than the optimal additive error in existing work. We complement our algorithm by showing if the unit-weight constraint does not apply, the lower bound for weight-level DP hierarchical clustering is essentially the same as the edge-level DP, i.e. $\Omega(n^2/\varepsilon)$ additive error. As a result, we also obtain a new lower bound of $\tilde{\Omega}(1/\varepsilon)$ additive error for balanced sparsest cuts in the weight-level DP model, which may be of independent interest. Finally, we evaluate our algorithm on synthetic and real-world datasets. Our experimental results show that our algorithm performs well in terms of extra cost and has good scalability to large graphs.

On Socially Fair Low-Rank Approximation and Column Subset Selection

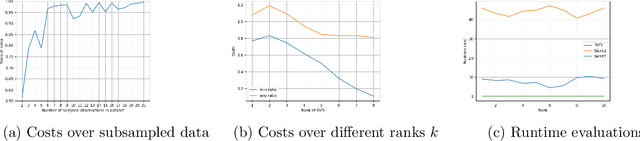
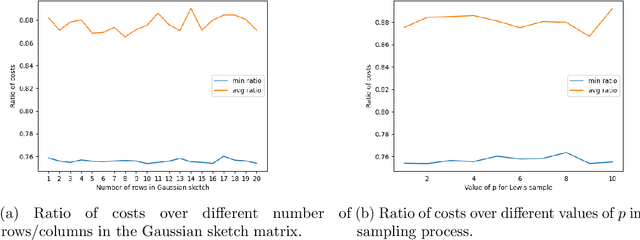
Low-rank approximation and column subset selection are two fundamental and related problems that are applied across a wealth of machine learning applications. In this paper, we study the question of socially fair low-rank approximation and socially fair column subset selection, where the goal is to minimize the loss over all sub-populations of the data. We show that surprisingly, even constant-factor approximation to fair low-rank approximation requires exponential time under certain standard complexity hypotheses. On the positive side, we give an algorithm for fair low-rank approximation that, for a constant number of groups and constant-factor accuracy, runs in $2^{\text{poly}(k)}$ time rather than the na\"{i}ve $n^{\text{poly}(k)}$, which is a substantial improvement when the dataset has a large number $n$ of observations. We then show that there exist bicriteria approximation algorithms for fair low-rank approximation and fair column subset selection that run in polynomial time.

On Approximability of $\ell_2^2$ Min-Sum Clustering

The $\ell_2^2$ min-sum $k$-clustering problem is to partition an input set into clusters $C_1,\ldots,C_k$ to minimize $\sum_{i=1}^k\sum_{p,q\in C_i}\|p-q\|_2^2$. Although $\ell_2^2$ min-sum $k$-clustering is NP-hard, it is not known whether it is NP-hard to approximate $\ell_2^2$ min-sum $k$-clustering beyond a certain factor. In this paper, we give the first hardness-of-approximation result for the $\ell_2^2$ min-sum $k$-clustering problem. We show that it is NP-hard to approximate the objective to a factor better than $1.056$ and moreover, assuming a balanced variant of the Johnson Coverage Hypothesis, it is NP-hard to approximate the objective to a factor better than 1.327. We then complement our hardness result by giving the first $(1+\varepsilon)$-coreset construction for $\ell_2^2$ min-sum $k$-clustering. Our coreset uses $\mathcal{O}\left(k^{\varepsilon^{-4}}\right)$ space and can be leveraged to achieve a polynomial-time approximation scheme with runtime $nd\cdot f(k,\varepsilon^{-1})$, where $d$ is the underlying dimension of the input dataset and $f$ is a fixed function. Finally, we consider a learning-augmented setting, where the algorithm has access to an oracle that outputs a label $i\in[k]$ for input point, thereby implicitly partitioning the input dataset into $k$ clusters that induce an approximately optimal solution, up to some amount of adversarial error $\alpha\in\left[0,\frac{1}{2}\right)$. We give a polynomial-time algorithm that outputs a $\frac{1+\gamma\alpha}{(1-\alpha)^2}$-approximation to $\ell_2^2$ min-sum $k$-clustering, for a fixed constant $\gamma>0$.

Fair Submodular Cover

Submodular optimization is a fundamental problem with many applications in machine learning, often involving decision-making over datasets with sensitive attributes such as gender or age. In such settings, it is often desirable to produce a diverse solution set that is fairly distributed with respect to these attributes. Motivated by this, we initiate the study of Fair Submodular Cover (FSC), where given a ground set $U$, a monotone submodular function $f:2^U\to\mathbb{R}_{\ge 0}$, a threshold $\tau$, the goal is to find a balanced subset of $S$ with minimum cardinality such that $f(S)\ge\tau$. We first introduce discrete algorithms for FSC that achieve a bicriteria approximation ratio of $(\frac{1}{\epsilon}, 1-O(\epsilon))$. We then present a continuous algorithm that achieves a $(\ln\frac{1}{\epsilon}, 1-O(\epsilon))$-bicriteria approximation ratio, which matches the best approximation guarantee of submodular cover without a fairness constraint. Finally, we complement our theoretical results with a number of empirical evaluations that demonstrate the effectiveness of our algorithms on instances of maximum coverage.

Private Vector Mean Estimation in the Shuffle Model: Optimal Rates Require Many Messages

We study the problem of private vector mean estimation in the shuffle model of privacy where $n$ users each have a unit vector $v^{(i)} \in\mathbb{R}^d$. We propose a new multi-message protocol that achieves the optimal error using $\tilde{\mathcal{O}}\left(\min(n\varepsilon^2,d)\right)$ messages per user. Moreover, we show that any (unbiased) protocol that achieves optimal error requires each user to send $\Omega(\min(n\varepsilon^2,d)/\log(n))$ messages, demonstrating the optimality of our message complexity up to logarithmic factors. Additionally, we study the single-message setting and design a protocol that achieves mean squared error $\mathcal{O}(dn^{d/(d+2)}\varepsilon^{-4/(d+2)})$. Moreover, we show that any single-message protocol must incur mean squared error $\Omega(dn^{d/(d+2)})$, showing that our protocol is optimal in the standard setting where $\varepsilon = \Theta(1)$. Finally, we study robustness to malicious users and show that malicious users can incur large additive error with a single shuffler.

Learning-Augmented Skip Lists

We study the integration of machine learning advice into the design of skip lists to improve upon traditional data structure design. Given access to a possibly erroneous oracle that outputs estimated fractional frequencies for search queries on a set of items, we construct a skip list that provably provides the optimal expected search time, within nearly a factor of two. In fact, our learning-augmented skip list is still optimal up to a constant factor, even if the oracle is only accurate within a constant factor. We show that if the search queries follow the ubiquitous Zipfian distribution, then the expected search time for an item by our skip list is only a constant, independent of the total number $n$ of items, i.e., $\mathcal{O}(1)$, whereas a traditional skip list will have an expected search time of $\mathcal{O}(\log n)$. We also demonstrate robustness by showing that our data structure achieves an expected search time that is within a constant factor of an oblivious skip list construction even when the predictions are arbitrarily incorrect. Finally, we empirically show that our learning-augmented skip list outperforms traditional skip lists on both synthetic and real-world datasets.

Fast $(1+\varepsilon)$-Approximation Algorithms for Binary Matrix Factorization

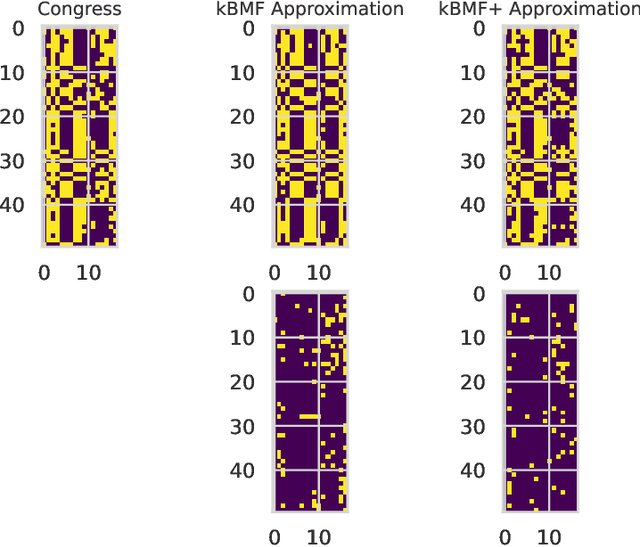
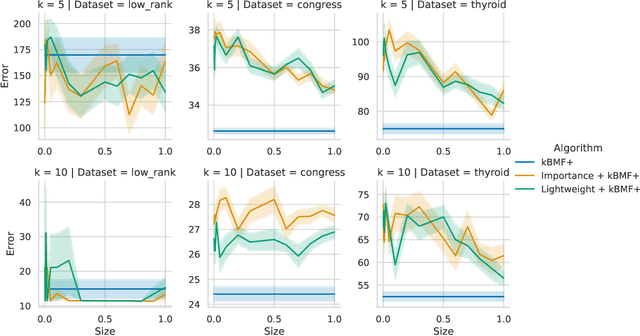
We introduce efficient $(1+\varepsilon)$-approximation algorithms for the binary matrix factorization (BMF) problem, where the inputs are a matrix $\mathbf{A}\in\{0,1\}^{n\times d}$, a rank parameter $k>0$, as well as an accuracy parameter $\varepsilon>0$, and the goal is to approximate $\mathbf{A}$ as a product of low-rank factors $\mathbf{U}\in\{0,1\}^{n\times k}$ and $\mathbf{V}\in\{0,1\}^{k\times d}$. Equivalently, we want to find $\mathbf{U}$ and $\mathbf{V}$ that minimize the Frobenius loss $\|\mathbf{U}\mathbf{V} - \mathbf{A}\|_F^2$. Before this work, the state-of-the-art for this problem was the approximation algorithm of Kumar et. al. [ICML 2019], which achieves a $C$-approximation for some constant $C\ge 576$. We give the first $(1+\varepsilon)$-approximation algorithm using running time singly exponential in $k$, where $k$ is typically a small integer. Our techniques generalize to other common variants of the BMF problem, admitting bicriteria $(1+\varepsilon)$-approximation algorithms for $L_p$ loss functions and the setting where matrix operations are performed in $\mathbb{F}_2$. Our approach can be implemented in standard big data models, such as the streaming or distributed models.