Instance-Optimality for Private KL Distribution Estimation

We study the fundamental problem of estimating an unknown discrete distribution $p$ over $d$ symbols, given $n$ i.i.d. samples from the distribution. We are interested in minimizing the KL divergence between the true distribution and the algorithm's estimate. We first construct minimax optimal private estimators. Minimax optimality however fails to shed light on an algorithm's performance on individual (non-worst-case) instances $p$ and simple minimax-optimal DP estimators can have poor empirical performance on real distributions. We then study this problem from an instance-optimality viewpoint, where the algorithm's error on $p$ is compared to the minimum achievable estimation error over a small local neighborhood of $p$. Under natural notions of local neighborhood, we propose algorithms that achieve instance-optimality up to constant factors, with and without a differential privacy constraint. Our upper bounds rely on (private) variants of the Good-Turing estimator. Our lower bounds use additive local neighborhoods that more precisely captures the hardness of distribution estimation in KL divergence, compared to ones considered in prior works.

Local Pan-Privacy for Federated Analytics

Pan-privacy was proposed by Dwork et al. as an approach to designing a private analytics system that retains its privacy properties in the face of intrusions that expose the system's internal state. Motivated by federated telemetry applications, we study local pan-privacy, where privacy should be retained under repeated unannounced intrusions on the local state. We consider the problem of monitoring the count of an event in a federated system, where event occurrences on a local device should be hidden even from an intruder on that device. We show that under reasonable constraints, the goal of providing information-theoretic differential privacy under intrusion is incompatible with collecting telemetry information. We then show that this problem can be solved in a scalable way using standard cryptographic primitives.

PREAMBLE: Private and Efficient Aggregation of Block Sparse Vectors and Applications

We revisit the problem of secure aggregation of high-dimensional vectors in a two-server system such as Prio. These systems are typically used to aggregate vectors such as gradients in private federated learning, where the aggregate itself is protected via noise addition to ensure differential privacy. Existing approaches require communication scaling with the dimensionality, and thus limit the dimensionality of vectors one can efficiently process in this setup. We propose PREAMBLE: Private Efficient Aggregation Mechanism for BLock-sparse Euclidean Vectors. PREAMBLE is a novel extension of distributed point functions that enables communication- and computation-efficient aggregation of block-sparse vectors, which are sparse vectors where the non-zero entries occur in a small number of clusters of consecutive coordinates. We then show that PREAMBLE can be combined with random sampling and privacy amplification by sampling results, to allow asymptotically optimal privacy-utility trade-offs for vector aggregation, at a fraction of the communication cost. When coupled with recent advances in numerical privacy accounting, our approach incurs a negligible overhead in noise variance, compared to the Gaussian mechanism used with Prio.

Privacy amplification by random allocation

We consider the privacy guarantees of an algorithm in which a user's data is used in $k$ steps randomly and uniformly chosen from a sequence (or set) of $t$ differentially private steps. We demonstrate that the privacy guarantees of this sampling scheme can be upper bound by the privacy guarantees of the well-studied independent (or Poisson) subsampling in which each step uses the user's data with probability $(1+ o(1))k/t $. Further, we provide two additional analysis techniques that lead to numerical improvements in some parameter regimes. The case of $k=1$ has been previously studied in the context of DP-SGD in Balle et al. (2020) and very recently in Chua et al. (2024). Privacy analysis of Balle et al. (2020) relies on privacy amplification by shuffling which leads to overly conservative bounds. Privacy analysis of Chua et al. (2024a) relies on Monte Carlo simulations that are computationally prohibitive in many practical scenarios and have additional inherent limitations.

Instance-Optimal Private Density Estimation in the Wasserstein Distance

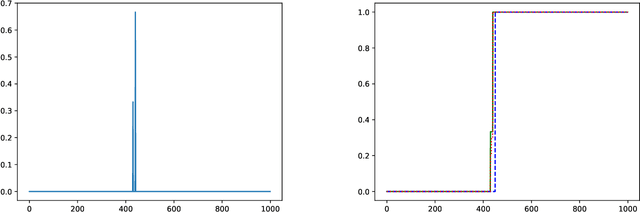
Estimating the density of a distribution from samples is a fundamental problem in statistics. In many practical settings, the Wasserstein distance is an appropriate error metric for density estimation. For example, when estimating population densities in a geographic region, a small Wasserstein distance means that the estimate is able to capture roughly where the population mass is. In this work we study differentially private density estimation in the Wasserstein distance. We design and analyze instance-optimal algorithms for this problem that can adapt to easy instances. For distributions $P$ over $\mathbb{R}$, we consider a strong notion of instance-optimality: an algorithm that uniformly achieves the instance-optimal estimation rate is competitive with an algorithm that is told that the distribution is either $P$ or $Q_P$ for some distribution $Q_P$ whose probability density function (pdf) is within a factor of 2 of the pdf of $P$. For distributions over $\mathbb{R}^2$, we use a different notion of instance optimality. We say that an algorithm is instance-optimal if it is competitive with an algorithm that is given a constant-factor multiplicative approximation of the density of the distribution. We characterize the instance-optimal estimation rates in both these settings and show that they are uniformly achievable (up to polylogarithmic factors). Our approach for $\mathbb{R}^2$ extends to arbitrary metric spaces as it goes via hierarchically separated trees. As a special case our results lead to instance-optimal private learning in TV distance for discrete distributions.

Private Vector Mean Estimation in the Shuffle Model: Optimal Rates Require Many Messages

We study the problem of private vector mean estimation in the shuffle model of privacy where $n$ users each have a unit vector $v^{(i)} \in\mathbb{R}^d$. We propose a new multi-message protocol that achieves the optimal error using $\tilde{\mathcal{O}}\left(\min(n\varepsilon^2,d)\right)$ messages per user. Moreover, we show that any (unbiased) protocol that achieves optimal error requires each user to send $\Omega(\min(n\varepsilon^2,d)/\log(n))$ messages, demonstrating the optimality of our message complexity up to logarithmic factors. Additionally, we study the single-message setting and design a protocol that achieves mean squared error $\mathcal{O}(dn^{d/(d+2)}\varepsilon^{-4/(d+2)})$. Moreover, we show that any single-message protocol must incur mean squared error $\Omega(dn^{d/(d+2)})$, showing that our protocol is optimal in the standard setting where $\varepsilon = \Theta(1)$. Finally, we study robustness to malicious users and show that malicious users can incur large additive error with a single shuffler.

Faster Convergence with Multiway Preferences

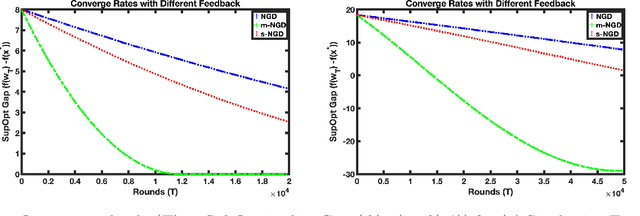
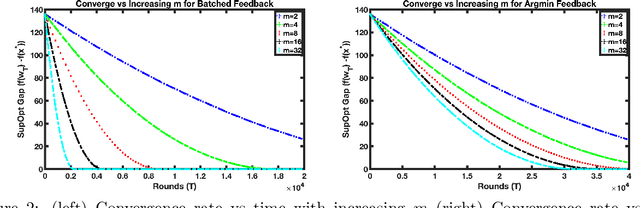
We address the problem of convex optimization with preference feedback, where the goal is to minimize a convex function given a weaker form of comparison queries. Each query consists of two points and the dueling feedback returns a (noisy) single-bit binary comparison of the function values of the two queried points. Here we consider the sign-function-based comparison feedback model and analyze the convergence rates with batched and multiway (argmin of a set queried points) comparisons. Our main goal is to understand the improved convergence rates owing to parallelization in sign-feedback-based optimization problems. Our work is the first to study the problem of convex optimization with multiway preferences and analyze the optimal convergence rates. Our first contribution lies in designing efficient algorithms with a convergence rate of $\smash{\widetilde O}(\frac{d}{\min\{m,d\} \epsilon})$ for $m$-batched preference feedback where the learner can query $m$-pairs in parallel. We next study a $m$-multiway comparison (`battling') feedback, where the learner can get to see the argmin feedback of $m$-subset of queried points and show a convergence rate of $\smash{\widetilde O}(\frac{d}{ \min\{\log m,d\}\epsilon })$. We show further improved convergence rates with an additional assumption of strong convexity. Finally, we also study the convergence lower bounds for batched preferences and multiway feedback optimization showing the optimality of our convergence rates w.r.t. $m$.

Federated Learning with Differential Privacy for End-to-End Speech Recognition

While federated learning (FL) has recently emerged as a promising approach to train machine learning models, it is limited to only preliminary explorations in the domain of automatic speech recognition (ASR). Moreover, FL does not inherently guarantee user privacy and requires the use of differential privacy (DP) for robust privacy guarantees. However, we are not aware of prior work on applying DP to FL for ASR. In this paper, we aim to bridge this research gap by formulating an ASR benchmark for FL with DP and establishing the first baselines. First, we extend the existing research on FL for ASR by exploring different aspects of recent $\textit{large end-to-end transformer models}$: architecture design, seed models, data heterogeneity, domain shift, and impact of cohort size. With a $\textit{practical}$ number of central aggregations we are able to train $\textbf{FL models}$ that are \textbf{nearly optimal} even with heterogeneous data, a seed model from another domain, or no pre-trained seed model. Second, we apply DP to FL for ASR, which is non-trivial since DP noise severely affects model training, especially for large transformer models, due to highly imbalanced gradients in the attention block. We counteract the adverse effect of DP noise by reviving per-layer clipping and explaining why its effect is more apparent in our case than in the prior work. Remarkably, we achieve user-level ($7.2$, $10^{-9}$)-$\textbf{DP}$ (resp. ($4.5$, $10^{-9}$)-$\textbf{DP}$) with a 1.3% (resp. 4.6%) absolute drop in the word error rate for extrapolation to high (resp. low) population scale for $\textbf{FL with DP in ASR}$.

Mean Estimation with User-level Privacy under Data Heterogeneity

A key challenge in many modern data analysis tasks is that user data are heterogeneous. Different users may possess vastly different numbers of data points. More importantly, it cannot be assumed that all users sample from the same underlying distribution. This is true, for example in language data, where different speech styles result in data heterogeneity. In this work we propose a simple model of heterogeneous user data that allows user data to differ in both distribution and quantity of data, and provide a method for estimating the population-level mean while preserving user-level differential privacy. We demonstrate asymptotic optimality of our estimator and also prove general lower bounds on the error achievable in the setting we introduce.

Samplable Anonymous Aggregation for Private Federated Data Analysis

We revisit the problem of designing scalable protocols for private statistics and private federated learning when each device holds its private data. Our first contribution is to propose a simple primitive that allows for efficient implementation of several commonly used algorithms, and allows for privacy accounting that is close to that in the central setting without requiring the strong trust assumptions it entails. Second, we propose a system architecture that implements this primitive and perform a security analysis of the proposed system.