Audra McMillan
Local Pan-Privacy for Federated Analytics
Mar 14, 2025Abstract:Pan-privacy was proposed by Dwork et al. as an approach to designing a private analytics system that retains its privacy properties in the face of intrusions that expose the system's internal state. Motivated by federated telemetry applications, we study local pan-privacy, where privacy should be retained under repeated unannounced intrusions on the local state. We consider the problem of monitoring the count of an event in a federated system, where event occurrences on a local device should be hidden even from an intruder on that device. We show that under reasonable constraints, the goal of providing information-theoretic differential privacy under intrusion is incompatible with collecting telemetry information. We then show that this problem can be solved in a scalable way using standard cryptographic primitives.
Private Selection with Heterogeneous Sensitivities
Jan 09, 2025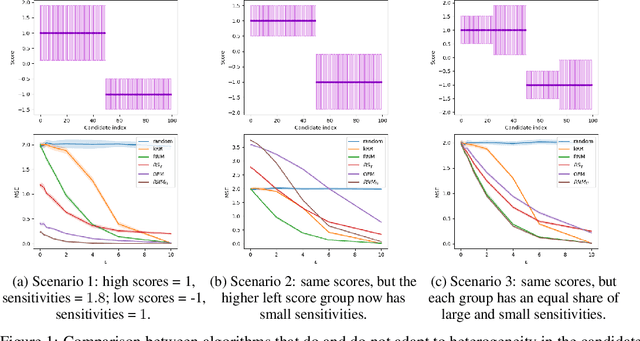
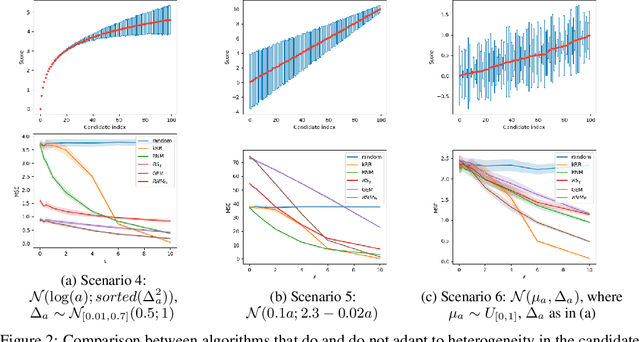
Abstract:Differentially private (DP) selection involves choosing a high-scoring candidate from a finite candidate pool, where each score depends on a sensitive dataset. This problem arises naturally in a variety of contexts including model selection, hypothesis testing, and within many DP algorithms. Classical methods, such as Report Noisy Max (RNM), assume all candidates' scores are equally sensitive to changes in a single individual's data, but this often isn't the case. To address this, algorithms like the Generalised Exponential Mechanism (GEM) leverage variability in candidate sensitivities. However, we observe that while these algorithms can outperform RNM in some situations, they may underperform in others - they can even perform worse than random selection. In this work, we explore how the distribution of scores and sensitivities impacts DP selection mechanisms. In all settings we study, we find that there exists a mechanism that utilises heterogeneity in the candidate sensitivities that outperforms standard mechanisms like RNM. However, no single mechanism uniformly outperforms RNM. We propose using the correlation between the scores and sensitivities as the basis for deciding which DP selection mechanism to use. Further, we design a slight variant of GEM, modified GEM that generally performs well whenever GEM performs poorly. Relying on the correlation heuristic we propose combined GEM, which adaptively chooses between GEM and modified GEM and outperforms both in polarised settings.
Instance-Optimal Private Density Estimation in the Wasserstein Distance
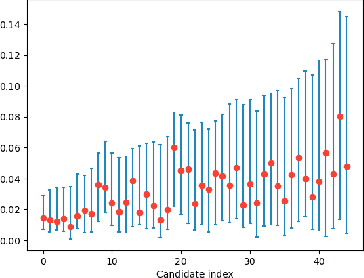
Jun 27, 2024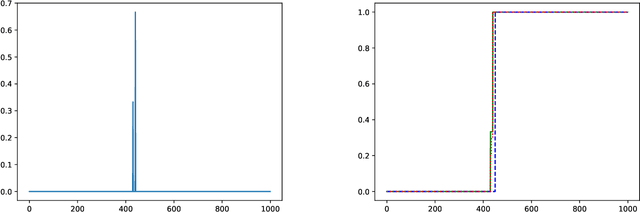
Abstract:Estimating the density of a distribution from samples is a fundamental problem in statistics. In many practical settings, the Wasserstein distance is an appropriate error metric for density estimation. For example, when estimating population densities in a geographic region, a small Wasserstein distance means that the estimate is able to capture roughly where the population mass is. In this work we study differentially private density estimation in the Wasserstein distance. We design and analyze instance-optimal algorithms for this problem that can adapt to easy instances. For distributions $P$ over $\mathbb{R}$, we consider a strong notion of instance-optimality: an algorithm that uniformly achieves the instance-optimal estimation rate is competitive with an algorithm that is told that the distribution is either $P$ or $Q_P$ for some distribution $Q_P$ whose probability density function (pdf) is within a factor of 2 of the pdf of $P$. For distributions over $\mathbb{R}^2$, we use a different notion of instance optimality. We say that an algorithm is instance-optimal if it is competitive with an algorithm that is given a constant-factor multiplicative approximation of the density of the distribution. We characterize the instance-optimal estimation rates in both these settings and show that they are uniformly achievable (up to polylogarithmic factors). Our approach for $\mathbb{R}^2$ extends to arbitrary metric spaces as it goes via hierarchically separated trees. As a special case our results lead to instance-optimal private learning in TV distance for discrete distributions.
Mean Estimation with User-level Privacy under Data Heterogeneity
Jul 28, 2023Abstract:A key challenge in many modern data analysis tasks is that user data are heterogeneous. Different users may possess vastly different numbers of data points. More importantly, it cannot be assumed that all users sample from the same underlying distribution. This is true, for example in language data, where different speech styles result in data heterogeneity. In this work we propose a simple model of heterogeneous user data that allows user data to differ in both distribution and quantity of data, and provide a method for estimating the population-level mean while preserving user-level differential privacy. We demonstrate asymptotic optimality of our estimator and also prove general lower bounds on the error achievable in the setting we introduce.
Samplable Anonymous Aggregation for Private Federated Data Analysis
Jul 27, 2023Abstract:We revisit the problem of designing scalable protocols for private statistics and private federated learning when each device holds its private data. Our first contribution is to propose a simple primitive that allows for efficient implementation of several commonly used algorithms, and allows for privacy accounting that is close to that in the central setting without requiring the strong trust assumptions it entails. Second, we propose a system architecture that implements this primitive and perform a security analysis of the proposed system.
Differentially Private Heavy Hitter Detection using Federated Analytics
Jul 21, 2023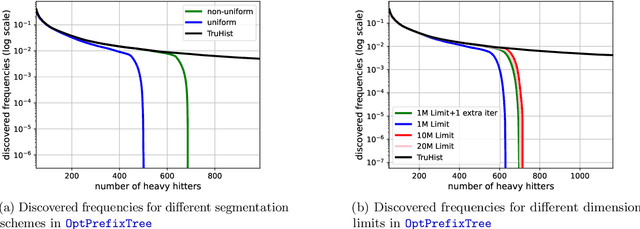
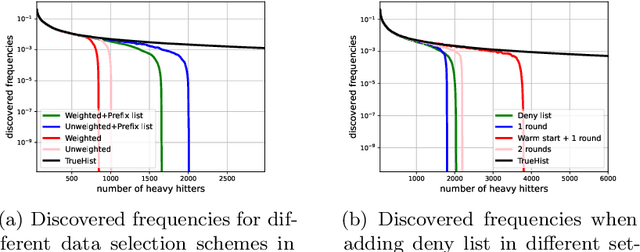

Abstract:In this work, we study practical heuristics to improve the performance of prefix-tree based algorithms for differentially private heavy hitter detection. Our model assumes each user has multiple data points and the goal is to learn as many of the most frequent data points as possible across all users' data with aggregate and local differential privacy. We propose an adaptive hyperparameter tuning algorithm that improves the performance of the algorithm while satisfying computational, communication and privacy constraints. We explore the impact of different data-selection schemes as well as the impact of introducing deny lists during multiple runs of the algorithm. We test these improvements using extensive experimentation on the Reddit dataset~\cite{caldas2018leaf} on the task of learning the most frequent words.
Instance-Optimal Differentially Private Estimation
Oct 28, 2022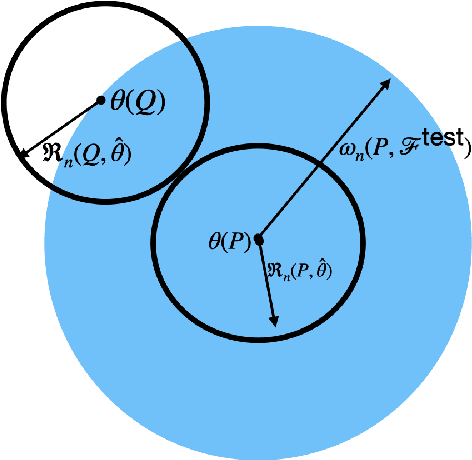
Abstract:In this work, we study local minimax convergence estimation rates subject to $\epsilon$-differential privacy. Unlike worst-case rates, which may be conservative, algorithms that are locally minimax optimal must adapt to easy instances of the problem. We construct locally minimax differentially private estimators for one-parameter exponential families and estimating the tail rate of a distribution. In these cases, we show that optimal algorithms for simple hypothesis testing, namely the recent optimal private testers of Canonne et al. (2019), directly inform the design of locally minimax estimation algorithms.
Stronger Privacy Amplification by Shuffling for Rényi and Approximate Differential Privacy
Aug 09, 2022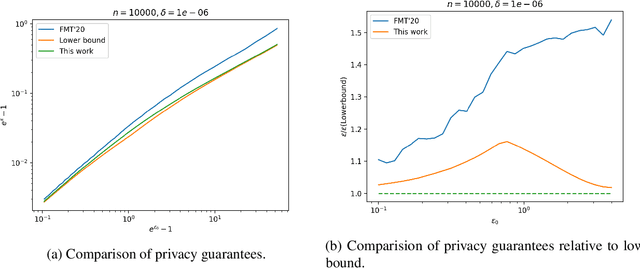
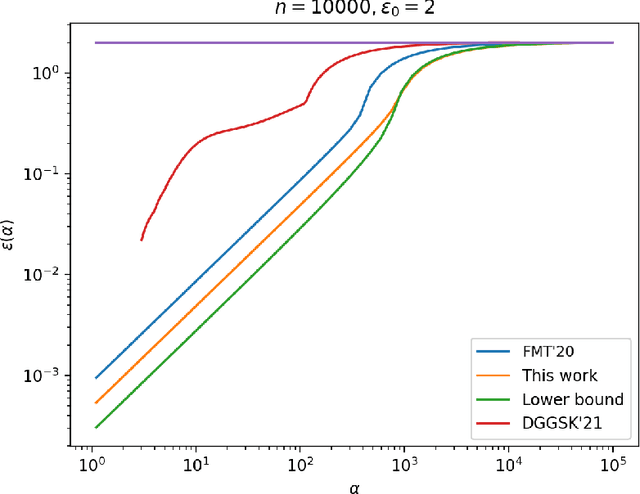
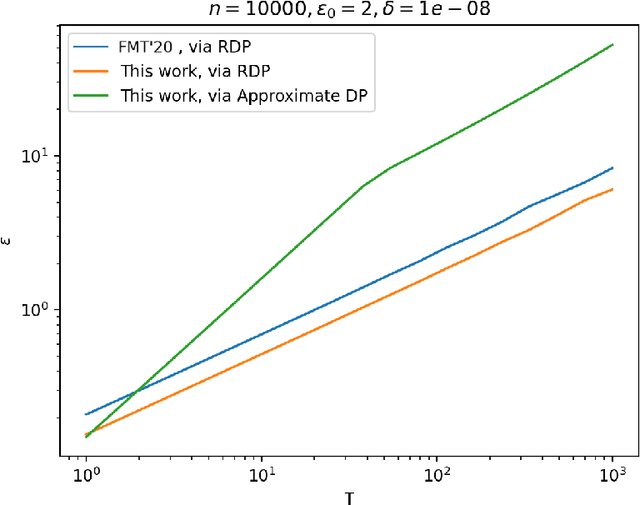
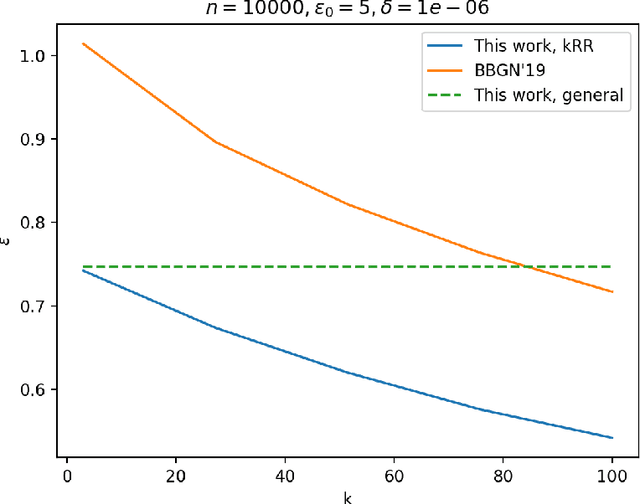
Abstract:The shuffle model of differential privacy has gained significant interest as an intermediate trust model between the standard local and central models [EFMRTT19; CSUZZ19]. A key result in this model is that randomly shuffling locally randomized data amplifies differential privacy guarantees. Such amplification implies substantially stronger privacy guarantees for systems in which data is contributed anonymously [BEMMRLRKTS17]. In this work, we improve the state of the art privacy amplification by shuffling results both theoretically and numerically. Our first contribution is the first asymptotically optimal analysis of the R\'enyi differential privacy parameters for the shuffled outputs of LDP randomizers. Our second contribution is a new analysis of privacy amplification by shuffling. This analysis improves on the techniques of [FMT20] and leads to tighter numerical bounds in all parameter settings.
Non-parametric Differentially Private Confidence Intervals for the Median
Jul 03, 2021
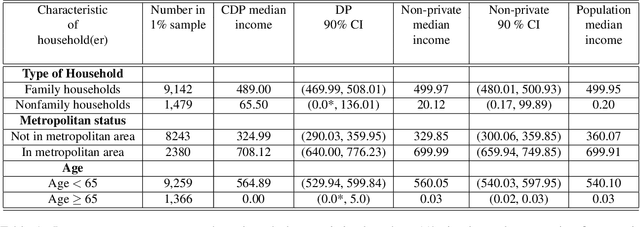

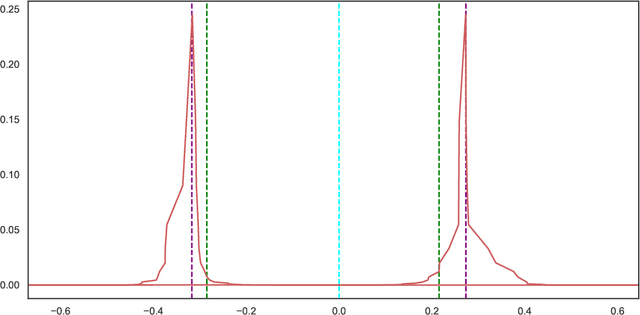
Abstract:Differential privacy is a restriction on data processing algorithms that provides strong confidentiality guarantees for individual records in the data. However, research on proper statistical inference, that is, research on properly quantifying the uncertainty of the (noisy) sample estimate regarding the true value in the population, is currently still limited. This paper proposes and evaluates several strategies to compute valid differentially private confidence intervals for the median. Instead of computing a differentially private point estimate and deriving its uncertainty, we directly estimate the interval bounds and discuss why this approach is superior if ensuring privacy is important. We also illustrate that addressing both sources of uncertainty--the error from sampling and the error from protecting the output--simultaneously should be preferred over simpler approaches that incorporate the uncertainty in a sequential fashion. We evaluate the performance of the different algorithms under various parameter settings in extensive simulation studies and demonstrate how the findings could be applied in practical settings using data from the 1940 Decennial Census.
Hiding Among the Clones: A Simple and Nearly Optimal Analysis of Privacy Amplification by Shuffling
Dec 25, 2020
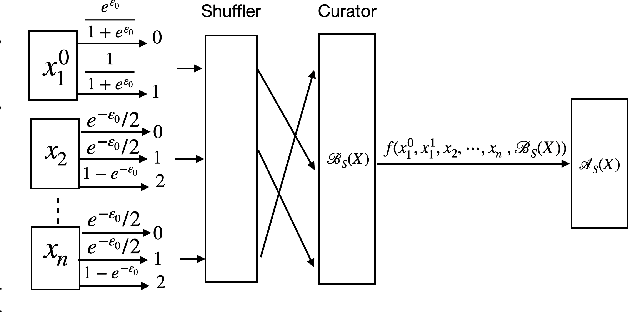
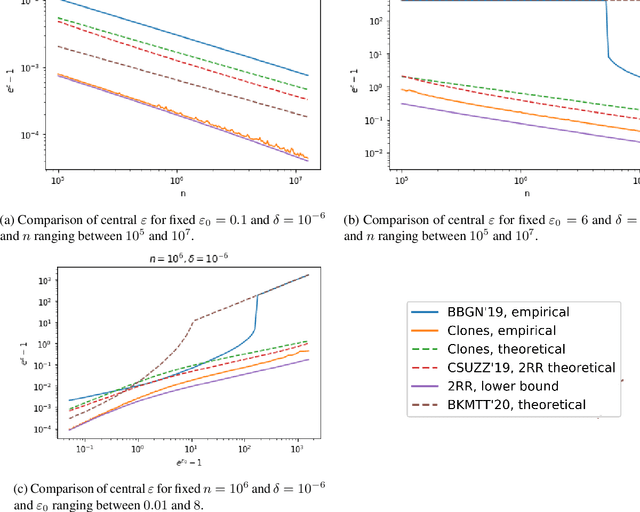
Abstract:Recent work of Erlingsson, Feldman, Mironov, Raghunathan, Talwar, and Thakurta [EFMRTT19] demonstrates that random shuffling amplifies differential privacy guarantees of locally randomized data. Such amplification implies substantially stronger privacy guarantees for systems in which data is contributed anonymously [BEMMRLRKTS17] and has lead to significant interest in the shuffle model of privacy [CSUZZ19,EFMRTT19]. We show that random shuffling of $n$ data records that are input to $\varepsilon_0$-differentially private local randomizers results in an $(O((1-e^{-\varepsilon_0})\sqrt{\frac{e^{\varepsilon_0}\log(1/\delta)}{n}}), \delta)$-differentially private algorithm. This significantly improves over previous work and achieves the asymptotically optimal dependence in $\varepsilon_0$. Our result is based on a new approach that is simpler than previous work and extends to approximate differential privacy with nearly the same guarantees. Our work also yields an empirical method to derive tighter bounds the resulting $\varepsilon$ and we show that it gets to within a small constant factor of the optimal bound. As a direct corollary of our analysis, we derive a simple and asymptotically optimal algorithm for discrete distribution estimation in the shuffle model of privacy. We also observe that our result implies the first asymptotically optimal privacy analysis of noisy stochastic gradient descent that applies to sampling without replacement.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge