Jayshree Sarathy
Non-parametric Differentially Private Confidence Intervals for the Median
Jul 03, 2021
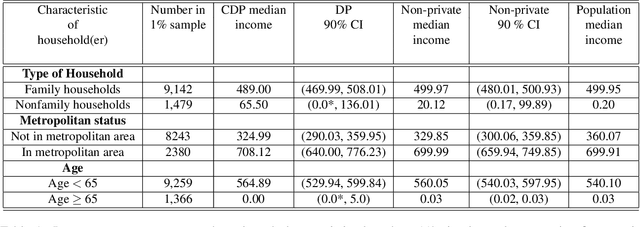

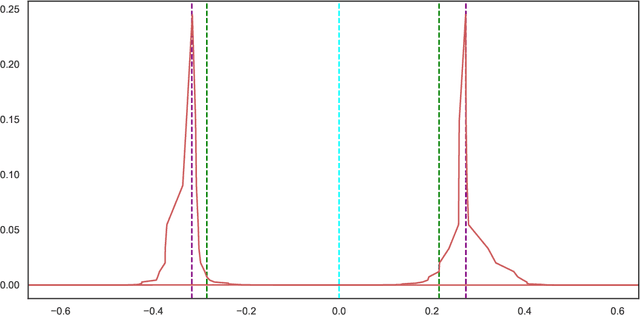
Abstract:Differential privacy is a restriction on data processing algorithms that provides strong confidentiality guarantees for individual records in the data. However, research on proper statistical inference, that is, research on properly quantifying the uncertainty of the (noisy) sample estimate regarding the true value in the population, is currently still limited. This paper proposes and evaluates several strategies to compute valid differentially private confidence intervals for the median. Instead of computing a differentially private point estimate and deriving its uncertainty, we directly estimate the interval bounds and discuss why this approach is superior if ensuring privacy is important. We also illustrate that addressing both sources of uncertainty--the error from sampling and the error from protecting the output--simultaneously should be preferred over simpler approaches that incorporate the uncertainty in a sequential fashion. We evaluate the performance of the different algorithms under various parameter settings in extensive simulation studies and demonstrate how the findings could be applied in practical settings using data from the 1940 Decennial Census.
Differentially Private Simple Linear Regression
Jul 10, 2020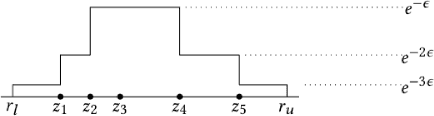
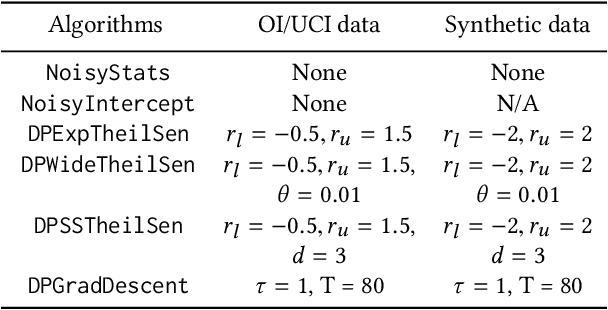
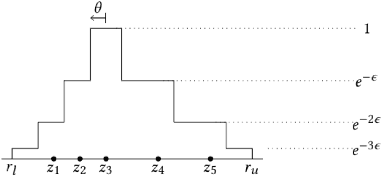
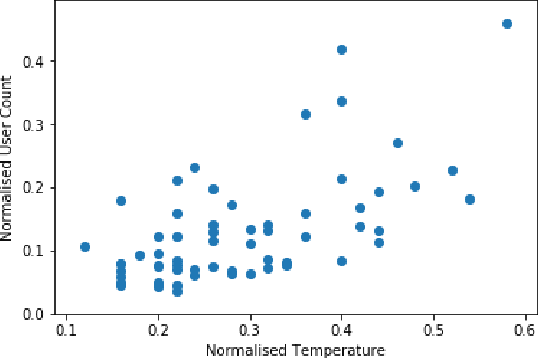
Abstract:Economics and social science research often require analyzing datasets of sensitive personal information at fine granularity, with models fit to small subsets of the data. Unfortunately, such fine-grained analysis can easily reveal sensitive individual information. We study algorithms for simple linear regression that satisfy differential privacy, a constraint which guarantees that an algorithm's output reveals little about any individual input data record, even to an attacker with arbitrary side information about the dataset. We consider the design of differentially private algorithms for simple linear regression for small datasets, with tens to hundreds of datapoints, which is a particularly challenging regime for differential privacy. Focusing on a particular application to small-area analysis in economics research, we study the performance of a spectrum of algorithms we adapt to the setting. We identify key factors that affect their performance, showing through a range of experiments that algorithms based on robust estimators (in particular, the Theil-Sen estimator) perform well on the smallest datasets, but that other more standard algorithms do better as the dataset size increases.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge