Membership Inference Attacks and Privacy in Topic Modeling

Recent research shows that large language models are susceptible to privacy attacks that infer aspects of the training data. However, it is unclear if simpler generative models, like topic models, share similar vulnerabilities. In this work, we propose an attack against topic models that can confidently identify members of the training data in Latent Dirichlet Allocation. Our results suggest that the privacy risks associated with generative modeling are not restricted to large neural models. Additionally, to mitigate these vulnerabilities, we explore differentially private (DP) topic modeling. We propose a framework for private topic modeling that incorporates DP vocabulary selection as a pre-processing step, and show that it improves privacy while having limited effects on practical utility.

Black-Box Training Data Identification in GANs via Detector Networks

Since their inception Generative Adversarial Networks (GANs) have been popular generative models across images, audio, video, and tabular data. In this paper we study whether given access to a trained GAN, as well as fresh samples from the underlying distribution, if it is possible for an attacker to efficiently identify if a given point is a member of the GAN's training data. This is of interest for both reasons related to copyright, where a user may want to determine if their copyrighted data has been used to train a GAN, and in the study of data privacy, where the ability to detect training set membership is known as a membership inference attack. Unlike the majority of prior work this paper investigates the privacy implications of using GANs in black-box settings, where the attack only has access to samples from the generator, rather than access to the discriminator as well. We introduce a suite of membership inference attacks against GANs in the black-box setting and evaluate our attacks on image GANs trained on the CIFAR10 dataset and tabular GANs trained on genomic data. Our most successful attack, called The Detector, involve training a second network to score samples based on their likelihood of being generated by the GAN, as opposed to a fresh sample from the distribution. We prove under a simple model of the generator that the detector is an approximately optimal membership inference attack. Across a wide range of tabular and image datasets, attacks, and GAN architectures, we find that adversaries can orchestrate non-trivial privacy attacks when provided with access to samples from the generator. At the same time, the attack success achievable against GANs still appears to be lower compared to other generative and discriminative models; this leaves the intriguing open question of whether GANs are in fact more private, or if it is a matter of developing stronger attacks.

Differentially Private Simple Linear Regression

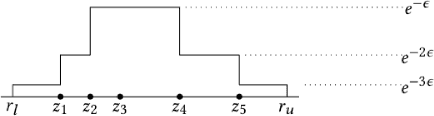
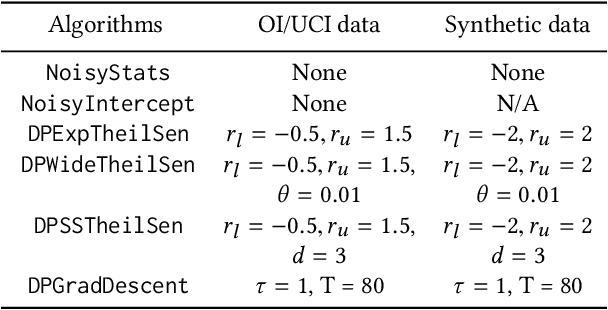
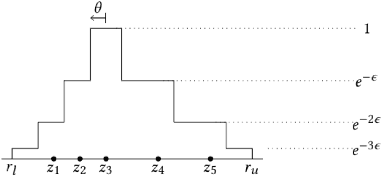
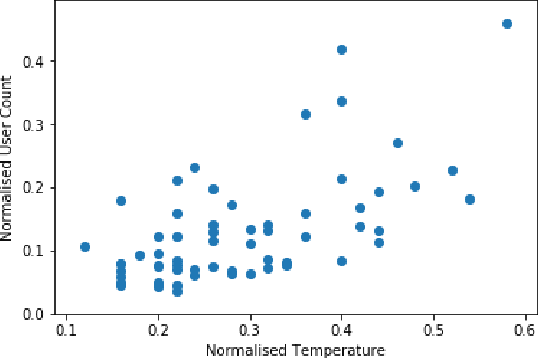
Economics and social science research often require analyzing datasets of sensitive personal information at fine granularity, with models fit to small subsets of the data. Unfortunately, such fine-grained analysis can easily reveal sensitive individual information. We study algorithms for simple linear regression that satisfy differential privacy, a constraint which guarantees that an algorithm's output reveals little about any individual input data record, even to an attacker with arbitrary side information about the dataset. We consider the design of differentially private algorithms for simple linear regression for small datasets, with tens to hundreds of datapoints, which is a particularly challenging regime for differential privacy. Focusing on a particular application to small-area analysis in economics research, we study the performance of a spectrum of algorithms we adapt to the setting. We identify key factors that affect their performance, showing through a range of experiments that algorithms based on robust estimators (in particular, the Theil-Sen estimator) perform well on the smallest datasets, but that other more standard algorithms do better as the dataset size increases.

Locating a Small Cluster Privately

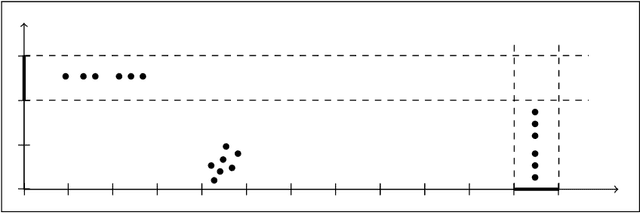
We present a new algorithm for locating a small cluster of points with differential privacy [Dwork, McSherry, Nissim, and Smith, 2006]. Our algorithm has implications to private data exploration, clustering, and removal of outliers. Furthermore, we use it to significantly relax the requirements of the sample and aggregate technique [Nissim, Raskhodnikova, and Smith, 2007], which allows compiling of "off the shelf" (non-private) analyses into analyses that preserve differential privacy.

Differentially Private Release and Learning of Threshold Functions

We prove new upper and lower bounds on the sample complexity of $(\epsilon, \delta)$ differentially private algorithms for releasing approximate answers to threshold functions. A threshold function $c_x$ over a totally ordered domain $X$ evaluates to $c_x(y) = 1$ if $y \le x$, and evaluates to $0$ otherwise. We give the first nontrivial lower bound for releasing thresholds with $(\epsilon,\delta)$ differential privacy, showing that the task is impossible over an infinite domain $X$, and moreover requires sample complexity $n \ge \Omega(\log^*|X|)$, which grows with the size of the domain. Inspired by the techniques used to prove this lower bound, we give an algorithm for releasing thresholds with $n \le 2^{(1+ o(1))\log^*|X|}$ samples. This improves the previous best upper bound of $8^{(1 + o(1))\log^*|X|}$ (Beimel et al., RANDOM '13). Our sample complexity upper and lower bounds also apply to the tasks of learning distributions with respect to Kolmogorov distance and of properly PAC learning thresholds with differential privacy. The lower bound gives the first separation between the sample complexity of properly learning a concept class with $(\epsilon,\delta)$ differential privacy and learning without privacy. For properly learning thresholds in $\ell$ dimensions, this lower bound extends to $n \ge \Omega(\ell \cdot \log^*|X|)$. To obtain our results, we give reductions in both directions from releasing and properly learning thresholds and the simpler interior point problem. Given a database $D$ of elements from $X$, the interior point problem asks for an element between the smallest and largest elements in $D$. We introduce new recursive constructions for bounding the sample complexity of the interior point problem, as well as further reductions and techniques for proving impossibility results for other basic problems in differential privacy.